Accessibility setting

2.1 Research Themes

The team develops constructive, function-theoretic approaches to inverse problems arising in modeling and design, in particular for electro-magnetic systems as well as in the analysis of certain classes of signals.

Data typically consist of measurements or desired behaviors. The general thread is to approximate them by families of solutions to the equations governing the underlying system. This leads us to consider various interpolation and approximation problems in classes of rational and meromorphic functions, harmonic gradients, or solutions to more general elliptic partial differential equations (PDE), in connection with inverse potential problems. A recurring difficulty is to control the singularities of the approximants.

The mathematical tools pertain to complex and harmonic analysis, approximation theory, potential theory, system theory, differential topology, optimization and computer algebra. Targeted applications include:

• identification and synthesis of analog microwave devices (filters, amplifiers),
• non-destructive control from field measurements in medical engineering (source recovery in magneto/electro encephalography), and paleomagnetism (determining the magnetization of rock samples).

In each case, the endeavor is to develop algorithms resulting in dedicated software.

3.1 Introduction

Within the extensive field of inverse problems, much of the research by Factas deals with reconstructing solutions of classical elliptic PDEs from their boundary behavior. Perhaps the simplest example lies with harmonic identification of a stable linear dynamical system: the transfer-function $f$ can be evaluated at a point $i\omega$ of the imaginary axis from the response to a periodic input at frequency $\omega$. Since $f$ is holomorphic in the right half-plane, it satisfies there the Cauchy-Riemann equation $\overline{\partial }f=0$, and recovering $f$ amounts to solve a Dirichlet problem which can be done in principle using, e.g. the Cauchy formula.

Practice is not nearly as simple, for $f$ is only measured pointwise in the pass-band of the system which makes the problem ill-posed  71. Moreover, the transfer function is usually sought in specific form, displaying the necessary physical parameters for control and design. For instance if $f$ is rational of degree $n$, then $\overline{\partial }f={\sum }_1^n{a}_j{\delta }_{z_j}$ where the $z_j$ are its poles and ${\delta }_{z_j}$ is a Dirac unit mass at $z_j$. Thus, to find the domain of holomorphy (i.e. to locate the $z_j$) amounts to solve a (degenerate) free-boundary inverse problem, this time on the left half-plane. To address such questions, the team has developed a two-step approach as follows.

• Step 1: To determine a complete model, that is, one which is defined at every frequency, in a sufficiently versatile function class (e.g. Hardy spaces). This ill-posed issue requires regularization, for instance constraints on the behavior at non-measured frequencies.
• Step 2: To compute a reduced order model. This typically consists of rational approximation of the complete model obtained in step 1, or phase-shift thereof to account for delays. We emphasize that deriving a complete model in step 1 is crucial to achieve stability of the reduced model in step 2.

Step 1 relates to extremal problems and analytic operator theory, see Section 3.3.1. Step 2 involves optimization, and some Schur analysis to parametrize transfer matrices of given Mc-Millan degree when dealing with systems having several inputs and outputs, see Section 3.3.2. It also makes contact with the topology of rational functions, in particular to count critical points and to derive bounds, see Section 3.3.2. Step 2 raises further issues in approximation theory regarding the rate of convergence and the extent to which singularities of the approximant (i.e. its poles) tend to singularities of the approximated function; this is where logarithmic potential theory becomes instrumental, see Section 3.3.3.

Applying a realization procedure to the result of step 2 yields an identification procedure from incomplete frequency data which was first demonstrated in  78 to tune resonant microwave filters. Harmonic identification of nonlinear systems around a stable equilibrium can also be envisaged by combining the previous steps with exact linearization techniques from  34.

A similar path can be taken to approach design problems in the frequency domain, replacing the measured behavior by some desired behavior. However, describing achievable responses in terms of the design parameters is often cumbersome, and most constructive techniques rely on specific criteria adapted to the physics of the problem. This is especially true of filters, the design of which traditionally appeals to polynomial extremal problems  74, 58. To this area, Apics contributed the use of Zolotarev-like problems for multi-band synthesis, although we presently favor interpolation techniques in which parameters arise in a more transparent manner, as well as convex relaxation of hyperbolic approximation problems, see Sections 3.2.2 and 6.2.

The previous example of harmonic identification quickly suggests a generalization of itself. Indeed, on identifying $ℂ$ with ${ℝ}^2$, holomorphic functions become conjugate-gradients of harmonic functions, so that harmonic identification is, after all, a special case of a classical issue: to recover a harmonic function on a domain from partial knowledge of the Dirichlet-Neumann data; when the portion of boundary where data are not available is itself unknown, we meet a free boundary problem. This framework for 2-D non-destructive control was first advocated in  63 and subsequently received considerable attention. It makes clear how to state similar problems in higher dimensions and for more general operators than the Laplacian, provided solutions are essentially determined by the trace of their gradient on part of the boundary which is the case for elliptic equations 1  32,  82. Such questions are particular instances of the so-called inverse potential problem, where a measure $\mu$ has to be recovered from the knowledge of the gradient of its potential (i.e., the field) on part of a hypersurface (a curve in 2-D) encompassing the support of $\mu$. For Laplace's operator, potentials are logarithmic in 2-D and Newtonian in higher dimensions. For elliptic operators with non constant coefficients, the potential depends on the form of fundamental solutions and is less manageable because it is no longer of convolution type. Nevertheless it is a useful concept bringing perspective on how problems could be raised and solved, using tools from harmonic analysis.

Inverse potential problems are severely indeterminate because infinitely many measures within an open set of ${ℝ}^n$ produce the same field outside this set; this phenomenon is called balayage  70. In the two steps approach previously described, we implicitly removed this indeterminacy by requiring in step 1 that the measure be supported on the boundary (because we seek a function holomorphic throughout the right half-space), and by requiring in step 2 that the measure be discrete in the left half-plane (in fact: a finite sum of point masses ${\sum }_1^N{a}_j{\delta }_{z_j}$). The discreteness assumption also prevails in 3-D inverse source problems, see Section 4.3. Conditions that ensure uniqueness of the solution to the inverse potential problem are part of the so-called regularizing assumptions which are needed in each case to derive efficient algorithms.

To recap, the gist of our approach is to approximate boundary data by (boundary traces of) fields arising from potentials of measures with specific support. This differs from standard approaches to inverse problems, where descent algorithms are applied to integration schemes of the direct problem; in such methods, it is the equation which gets approximated (in fact: discretized).

Along these lines, Factas advocates the use of steps 1 and 2 above, along with some singularity analysis, to approach issues of nondestructive control in 2-D and 3-D 2,  41, 45. The team is currently engaged in the generalization to inverse source problems for the Laplace equation in 3-D, to be described further in Section 3.2.1. There, holomorphic functions are replaced by harmonic gradients; applications are to inverse source problems in neurosciences (in particular in EEG/MEG) and inverse magnetization problems in geosciences, see Section 4.3.

The approximation-theoretic tools developed by Apics and now by Factas to handle issues mentioned so far are outlined in Section 3.3. In Section 3.2 to come, we describe in more detail which problems are considered and which applications are targeted.

3.2 Range of inverse problems

3.3 Approximation

Participants: Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Martine Olivi, Fabien Seyfert.

3.4 Software tools of the team

In addition to the above-mentioned research activities, Factas develops and maintains a number of long-term software tools that either implement and illustrate effectiveness of the algorithms theoretically developed by the team or serve as tools to help further research by team members. We present briefly the most important of them.

4.1 Introduction

Application domains are naturally linked to the problems described in Sections 3.2.1 and 3.2.2. By and large, they split into a systems-and-circuits part and an inverse-source-and-boundary-problems part, united under a common umbrella of function-theoretic techniques as described in Section 3.3.

4.2 Inverse magnetization problems

Participants: Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Konstantinos Mavreas.

To set up the context, recall that the Earth's geomagnetic field is generated by convection of the liquid metallic core (geodynamo) and that rocks become magnetized by the ambient field as they are formed or after subsequent alteration. Their remanent magnetization provides records of past variations of the geodynamo, which is used to study important processes in Earth sciences like motion of tectonic plates and geomagnetic reversals. Rocks from Mars, the Moon, and asteroids also contain remanent magnetization which indicates the past presence of core dynamos. Magnetization in meteorites may even record fields produced by the young sun and the protoplanetary disk which may have played a key role in solar system formation.

For a long time, paleomagnetic techniques were only capable of analyzing bulk samples and compute their net magnetic moment. The development of SQUID microscopes has recently extended the spatial resolution to sub-millimeter scales, raising new physical and algorithmic challenges. The associate team Impinge aims at tackling them, experimenting with the SQUID microscope set up in the Paleomagnetism Laboratory of the department of Earth, Atmospheric and Planetary Sciences at MIT. Typically, pieces of rock are sanded down to a thin slab, and the magnetization has to be recovered from the field measured on a planar region at small distance from the slab.

Mathematically speaking, both inverse source problems for EEG from Section 4.3 and inverse magnetization problems described presently amount to recover the (3-D valued) quantity $m$ (primary current density in case of the brain or magnetization in case of a thin slab of rock) from measurements of the potential:

outside the volume $\Omega$ of the object. Depending on the geometry of models, the magnetization distribution $m$ may lie in a volume or spread out on a surface. This results in quite different identifiability properties, see  37 and Section 6.1.1, but the two situations share a substantial mathematical common core.

Another timely instance of inverse magnetization problems lies with geomagnetism. Satellites orbiting around the Earth measure the magnetic field at many points, and nowadays it is a challenge to extract global information from those measurements. In collaboration with C. Gerhards (Geomathematics and Geoinformatics Group, Technische Universität Bergakademie Freiberg, Germany), we started to work on the problem of separating the magnetic field due to the magnetization of the globe's crust from the magnetic field due to convection in the liquid metallic core. The techniques involved are variants, in a spherical context, from those developed within the Impinge associate team for paleomagnetism, see Section 6.1.1.

4.3 Inverse source problems in EEG

Participants: Paul Asensio, Laurent Baratchart, Juliette Leblond, Jean-Paul Marmorat, Masimba Nemaire.

Solving overdetermined Cauchy problems for the Laplace equation on a spherical layer (in 3-D) in order to extrapolate incomplete data (see Section 3.2.1) is a necessary ingredient of the team's approach to inverse source problems, in particular for applications to EEG, see 9. Indeed, the latter involves propagating the initial conditions through several layers of different conductivities, from the boundary shell down to the center of the domain where the singularities (i.e. the sources) lie. Once propagated to the innermost sphere, it turns out that traces of the boundary data on 2-D cross sections coincide with analytic functions with branched singularities in the slicing plane 7,  42. The singularities are related to the actual location of the sources, namely their moduli reach in turn a maximum when the plane contains one of the sources. Hence we are back to the 2-D framework of Section 3.3.3, and recovering these singularities can be performed via best rational approximation. The goal is to produce a fast and sufficiently accurate initial guess on the number and location of the sources in order to run heavier descent algorithms on the direct problem, which are more precise but computationally costly and often fail to converge if not properly initialized. Our belief is that such a localization process can add a geometric, valuable piece of information to the standard temporal analysis of EEG signal records.

Numerical experiments obtained with our software FindSources3D give very good results on simulated data and we are now engaged in the process of handling real experimental data, simultaneously recorded by EEG and MEG devices, in collaboration with our partners at INS, hospital la Timone, Marseille (see Section 6.1.3).

Furthermore, another approach is being studied for EEG, that consists in regularizing the inverse source problem by a total variation constraint on the source term (a measure), added to the quadratic data approximation criterion. It is similar to the path that is taken for inverse magnetization problems (see Sections 4.2 and 6.1.1), and it presently focuses on surface-distributed models.

4.4 Identification and design of microwave devices

Participants: Laurent Baratchart, Sylvain Chevillard, Jean-Paul Marmorat, Martine Olivi, Fabien Seyfert.

One of the best training grounds for function-theoretic applications by the team is the identification and design of physical systems whose performance is assessed frequency-wise. This is the case of electromagnetic resonant systems which are of common use in telecommunications.

In space telecommunications (satellite transmissions), constraints specific to on-board technology lead to the use of filters with resonant cavities in the microwave range. These filters serve multiplexing purposes (before or after amplification), and consist of a sequence of cylindrical hollow bodies, magnetically coupled by irises (orthogonal double slits). The electromagnetic wave that traverses the cavities satisfies the Maxwell equations, forcing the tangent electrical field along the body of the cavity to be zero. A deeper study of the Helmholtz equation states that an essentially discrete set of wave vectors is selected. In the considered range of frequency, the electrical field in each cavity can be decomposed along two orthogonal modes, perpendicular to the axis of the cavity (other modes are far off in the frequency domain, and their influence can be neglected).

Each cavity (see Figure 1) has three screws, horizontal, vertical and midway (horizontal and vertical are two arbitrary directions, the third direction makes an angle of 45 or 135 degrees, the easy case is when all cavities show the same orientation, and when the directions of the irises are the same, as well as the input and output slits). Since screws are conductors, they behave as capacitors; besides, the electrical field on the surface has to be zero, which modifies the boundary conditions of one of the two modes (for the other mode, the electrical field is zero hence it is not influenced by the screw), the third screw acts as a coupling between the two modes. The effect of an iris is opposite to that of a screw: no condition is imposed on a hole, which results in a coupling between two horizontal (or two vertical) modes of adjacent cavities (in fact the iris is the union of two rectangles, the important parameter being their width). The design of a filter consists in finding the size of each cavity, and the width of each iris. Subsequently, the filter can be constructed and tuned by adjusting the screws. Finally, the screws are glued once a satisfactory response has been obtained. In what follows, we shall consider a typical example, a filter designed by the CNES in Toulouse, with four cavities near 11 GHz.

Near the resonance frequency, a good approximation to the Helmholtz equations is given by a second order differential equation. Thus, one obtains an electrical model of the filter as a sequence of electrically-coupled resonant circuits, each circuit being modeled by two resonators, one per mode, the resonance frequency of which represents the frequency of a mode, and whose resistance accounts for electric losses (surface currents) in the cavities.

This way, the filter can be seen as a quadripole, with two ports, when plugged onto a resistor at one end and fed with some potential at the other end. One is now interested in the power which is transmitted and reflected. This leads one to define a scattering matrix $S$, which may be considered as the transfer function of a stable causal linear dynamical system, with two inputs and two outputs. Its diagonal terms $S_{1,1}$, $S_{2,2}$ correspond to reflections at each port, while $S_{1,2}$, $S_{2,1}$ correspond to transmission. These functions can be measured at certain frequencies (on the imaginary axis). The matrix $S$ is approximately rational of order 4 times the number of cavities (that is 16 in the example on Figure 2), and the key step consists in expressing the components of the equivalent electrical circuit as functions of the $S_{ij}$ (since there are no formulas expressing the lengths of the screws in terms of parameters of this electrical model). This representation is also useful to analyze the numerical simulations of the Maxwell equations, and to check the quality of a design, in particular the absence of higher resonant modes.

In fact, resonance is not studied via the electrical model, but via a low-pass equivalent circuit obtained upon linearizing near the central frequency, which is no longer conjugate symmetric (i.e. the underlying system may no longer have real coefficients) but whose degree is divided by 2 (8 in the example).

In short, the strategy for identification is as follows:

• measuring the scattering matrix of the filter near the optimal frequency over twice the pass band (which is 80MHz in the example).
• Solving bounded extremal problems for the transmission and the reflection (the modulus of he response being respectively close to 0 and 1 outside the interval measurement, cf. Section 3.3.1) in order to get a models for the scattering matrix as an analytic matrix-valued function. This provides us with a scattering matrix known to be close to a rational matrix of order roughly 1/4 of the number of data points.
• Approximating this scattering matrix by a true rational transfer-function of appropriate degree (8 in this example) via the Endymion or RARL2 software (cf. Section 3.3.2).
• A state space realization of $S$, viewed as a transfer function, can then be obtained, where additional symmetry constraints coming from the reciprocity law and possibly other physical features of the device have to be imposed.
• Finally one builds a realization of the approximant and looks for a change of variables that eliminates non-physical couplings. This is obtained by using algebraic-solvers and continuation algorithms on the group of orthogonal complex matrices (symmetry forces this type of transformation).

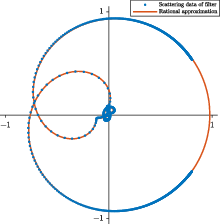
The final approximation is of high quality. This can be interpreted as a confirmation of the linearity assumption on the system: the relative $L^2$ error is less than ${10}^{-3}$. This is illustrated by a reflection diagram (Figure 2).

The above considerations are valid for a large class of filters. These developments have also been used for the design of non-symmetric filters, which are useful for the synthesis of repeating devices.

The team further investigates problems relative to the design of optimal responses for microwave devices. The resolution of a quasi-convex Zolotarev problems was proposed, in order to derive guaranteed optimal multi-band filter responses subject to modulus constraints  72. This generalizes the classical single band design techniques based on Chebyshev polynomials and elliptic functions. The approach relies on the fact that the modulus of the scattering parameter $|S_{1,2}|$ admits a simple expression in terms of the filtering function $D=|S_{1,1}|/|S_{1,2}|$, namely

The filtering function appears to be the ratio of two polynomials $p_1/p_2$, the numerator of the reflection and transmission scattering factors, that may be chosen freely. The denominator $q$ is then obtained as the unique stable unitary polynomial solving the classical Feldtkeller spectral equation:

The relative simplicity of the derivation of a filter's response, under modulus constraints, owes much to the possibility of forgetting about Feldtkeller's equation and express all design constraints in terms of the filtering function. This no longer the case when considering the synthesis $N$-port devices for $N>3$, like multiplexers, routers and power dividers, or when considering the synthesis of filters under matching conditions. The efficient derivation of multiplexers responses is the subject of recent investigation by Factas, using techniques based on constrained Nevanlinna-Pick interpolation (see Section 6.2).

Through contacts with CNES (Toulouse) and UPV (Bilbao), Apics got additionally involved in the design of amplifiers which, unlike filters, are active devices. A prominent issue here is stability. A twenty years back, it was not possible to simulate unstable responses, and only after building a device could one detect instability. The advent of so-called harmonic balance techniques, which compute steady state responses of linear elements in the frequency domain and look for a periodic state in the time domain of a network connecting these linear elements via static non-linearities made it possible to compute the harmonic response of a (possibly nonlinear and unstable) device  81. This has had tremendous impact on design, and there is a growing demand for software analyzers. The team is also becoming active in this area.

In this connection, there are two types of stability involved. The first is stability of a fixed point around which the linearized transfer function accounts for small signal amplification. The second is stability of a limit cycle which is reached when the input signal is no longer small and truly nonlinear amplification is attained (e.g. because of saturation). Applications by the team so far have been concerned with the first type of stability, and emphasis is put on defining and extracting the “unstable part” of the response, see Section 6.4. The stability check for limit cycles has made important theoretical advances, and numerical algorithms are now under investigation.

5.1 Footprint of research activities

In coordination with Céline Serrano, who is in charge of “Sustainable development” at the national level, Sylvain Chevillard and Martine Olivi participated with a few volunteers from other Inria research centers to an effort of establishing the carbon footprint of their team. The goals were manifolds:

• Identify the data necessary to collect, and more generally, spot the difficulties of this exercise.
• Subsequently propose a methodology and, possibly, automated tools to compute the carbon footprint of an Inria team, in view of generalizing this computation to as many teams as possible.
• Get an overview of the share of the different sources of emission in the overall carbon footprint of the team, so as to spot what sources would be the easiest to reduce.
• Get a first footprint that would serve as a reference for the subsequent years, in order to be able to quantify the effects of a reduction policy that the team would adopt.

The carbon footprint has been evaluated for year 2019 since the data for the complete year were available. The team was then composed of 5 permanent researchers, 7 PhD students and post-docs (some of them starting during the year) and one assistant (shared with another team). Of a total of roughly 21 tons of ${\text{CO}}_{2\text{e}}$, the figures are the following:

• 1/3 comes from the commutes between home and travel place2;
• a bit less than 1/3 comes from the mission travels;
• 1/6 comes from the meals taken at the cafeteria;
• the remaining part (a bit more than 1/6) comes half from the gray energy of the equipment (the energy used to construct them and handle their end of life) and half from the energy used in the offices (heating/cooling/light/powering of computers).

A report is currently being written to explain the methodology used and give the precise figures.

The outcome of this effort is also a prototype of tool to collect in a fairly automated way the information regarding the missions and the equipment. Also a survey has been designed for gathering the information about the commute travels and eating habits of the members of a team. This survey can be reused by other teams in the future.

The pandemic crisis prevented us from discussing collectively these results in detail and think of strategies of reduction. It must be noted however that 2020, because of the generalization of teleworking and the absence of missions, is a radical example of what can be done to significantly reduce the carbon footprint of the team.

6.1 Inverse problems for Poisson-Laplace equations

Participants: Paul Asensio, Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Jean-Paul Marmorat, Konstantinos Mavreas, Masimba Nemaire.

6.1.1 Inverse magnetization issues for planar samples

The goal is to invert magnetizations carried by a planar set in Euclidean space from measurements of the magnetic field nearby. A typical application is to paleomagnetism, to determine magnetic properties of rock samples, shaped into thin slabs, with measurements taken by a superconducting quantum interference device (SQUID). Figure 3 sketches the corresponding experimental set up, brought up to our knowledge by collaborators from the Earth and Planetary Sciences Laboratory at MIT.

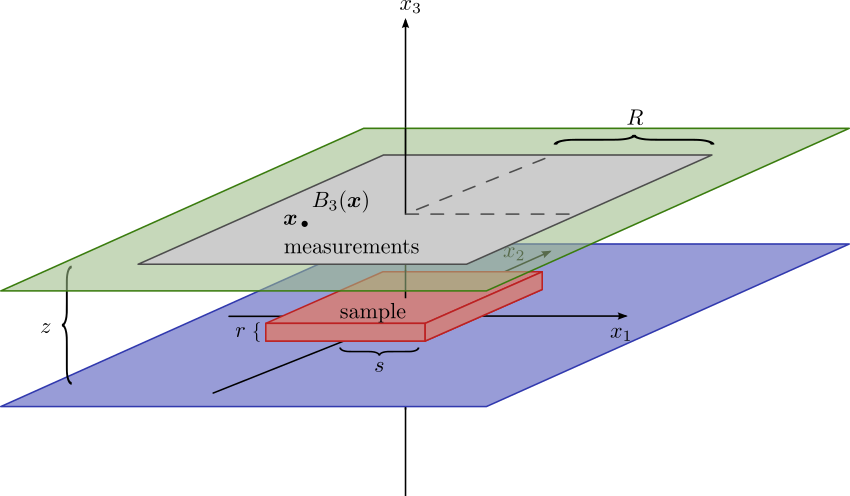
Figure 3 presents a schematic view of the experimental setup: the sample lies on a horizontal plane at height 0 and its support is included in a parallelepiped. The vertical component $B_3$ of the field produced by the sample is measured in points of a horizontal square at height $z$.

We pursued our investigation of the recovery of magnetizations modeled by signed measures on thin samples which is an instance of Poisson inverse problem with right hand side in divergence form (the divergence of a ${ℝ}^3$-valued measure supported on a planar set in space). We showed in previous years that consistent recovery is possible, in the Morozov discrepancy limit, by penalizing the total variation, when either the support of the magnetization is purely 1-unrectifiable (which holds in particular for dipolar models) or the magnetization is unidirectional (an assumption of physical interest because igneous rocks acquire magnetization by cooling down in some ambient field). This year we have shown that magnetizations supported on sufficiently separated line segments also enjoy consistent recovery in the sense mentioned above, and we were able to give nontrivial examples. These notions play a role similar to sparsity in this infinite-dimensional context. An article has been submitted to report on these results 24. A consistent discretization of these results, obtained in a continuous setting, is made possible by the fact that the argument of the minimum of the regularized criterion $\parallel f-B_3{\mu \parallel }_2^2+\lambda {\parallel \mu \parallel }_{TV}$ is unique; here, $\mu$ is the measure representing the magnetization with respect to which the criterion gets optimized, $f$ is the data and $\lambda >0$ a regularization parameter, while ${\parallel \mu \parallel }_{TV}$ is the total variation of $\mu$. This uniqueness result is proven using the particular form of the critical point equation for the criterion, together with a loop decomposition of planar divergence free measures which sharpens in the 2-D setting the structure theorem of 79. An implementation using a variant of the FISTA algorithm has been set up which yields interesting results. This is collaborative research with D. Hardin from Vanderbilt university and H. Haddar and C. Villalobos-Guillén from the team DEFI (Inria Saclay).

We studied in 16 an inverse problem that consists in estimating the first (zero-order) moment of some ${ℝ}^2$-valued distribution $\mu$ supported within a closed interval $S\subset ℝ$, from partial knowledge of the solution to the Poisson-Laplace partial differential equation with source term equal to the divergence of $\mu$ on another interval parallel to and located at some distance from $S$. Such a question coincides with a 2-D version of an inverse magnetic “net” moment recovery question that also arises in paleomagnetism, for thin rock samples. We constructively solved a best approximation problem under a quadratic constraint and in Sobolev spaces involving the restriction of the Poisson extension of the divergence of $\mu$. Numerical results obtained from the described algorithms for the net moment approximation are also furnished.

6.1.2 Inverse magnetization issues from sparse cylindrical data

The team Factas was a partner of the ANR project MagLune on Lunar magnetism, headed by the Geophysics and Planetology Department of Cerege, CNRS, Aix-en-Provence, which ended last year. Recent studies let geoscientists think that the Moon used to have a magnetic dynamo for a while. However, the exact process that triggered and fed this dynamo is still not understood, much less why it stopped. The overall goal of the project was to devise models to explain how this dynamo phenomenon was possible on the Moon.

The geophysicists from Cerege went a couple of times to NASA to perform measurements on a few hundreds of samples brought back from the Moon by Apollo missions. The samples are kept inside bags with a protective atmosphere, and geophysicists are not allowed to open the bags, nor to take out samples from NASA facilities. Moreover, the process must be carried out efficiently as a fee is due to NASA by the time when handling these moon samples. Therefore, measurements were performed with some specific magnetometer designed by our colleagues from Cerege. This device measures the components of the magnetic field produced by the sample, at some discrete set of points located on circles belonging to three cylinders (see Figure 4). The objective of Factas is to enhance the numerical efficiency of post-processing data obtained with this magnetometer.

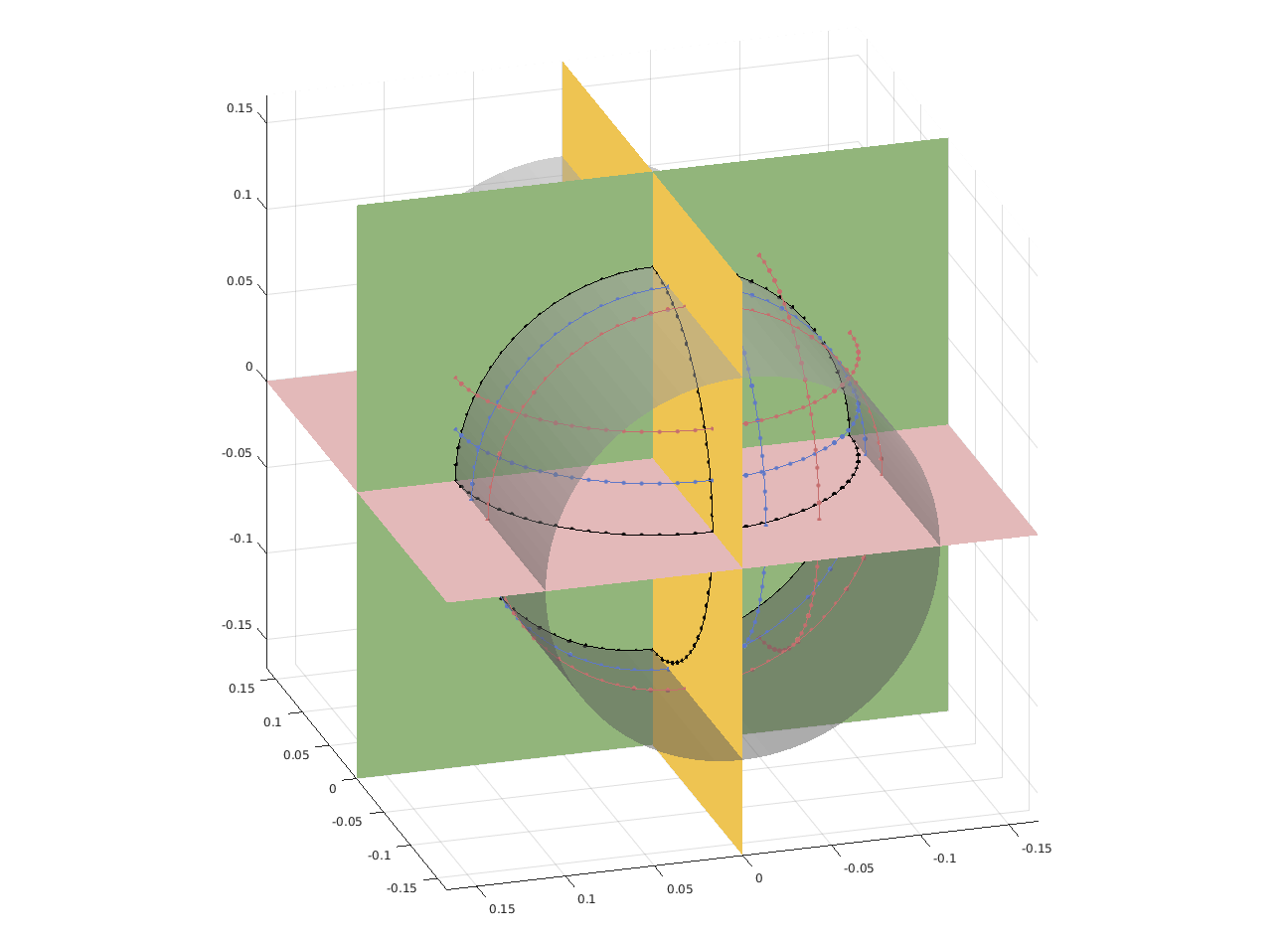
Under the hypothesis that the field can be well explained by a single magnetic pointwise dipole, and using ideas similar to those underlying the FindSources3D tool (see Sections 3.4.3 and 6.1.3), we try to recover the position and the moment of the dipole using the available measurements. This work, which is still on-going, constituted the topic of the PhD thesis of K. Mavreas, 21 defended on January 31, 2020.

6.1.3 Inverse problems in medical imaging

In 3-D, functional or clinically active regions in the cortex are often modeled by pointwise sources that have to be localized from measurements, taken by electrodes on the scalp, of an electrical potential satisfying a Laplace equation (EEG, electroencephalography). In the works 7, 42 on the behavior of poles in best rational approximants of fixed degree to functions with branch points, it was shown how to proceed via best rational approximation on a sequence of 2-D disks cut along the inner sphere, for the case where there are finitely many sources (see Section 4.3).

In this connection, a dedicated software FindSources3D (FS3D, see Section 3.4.3) is being developed, in collaboration with the Inria team Athena and the CMA - Mines ParisTech. Its Matlab version now incorporates the treatment of MEG data, the aim being to handle simultaneous EEG–MEG recordings available from our partners at INS, hospital la Timone, Marseille. Indeed, it is now possible to use simultaneously EEG and MEG measurement devices, in order to measure both the electrical potential and a component of the magnetic field (its normal component on the MEG helmet, that can be assumed to be spherical). Solving the inverse source problem from joint EEG and MEG data actually improves accuracy of the source estimation.

From synthetic data simulated with MNE3, that consist in two asynchronous source patches (in the visual cortex), FS3D furnishes the results shown in Figure 5 where they are mapped in a realistic head.

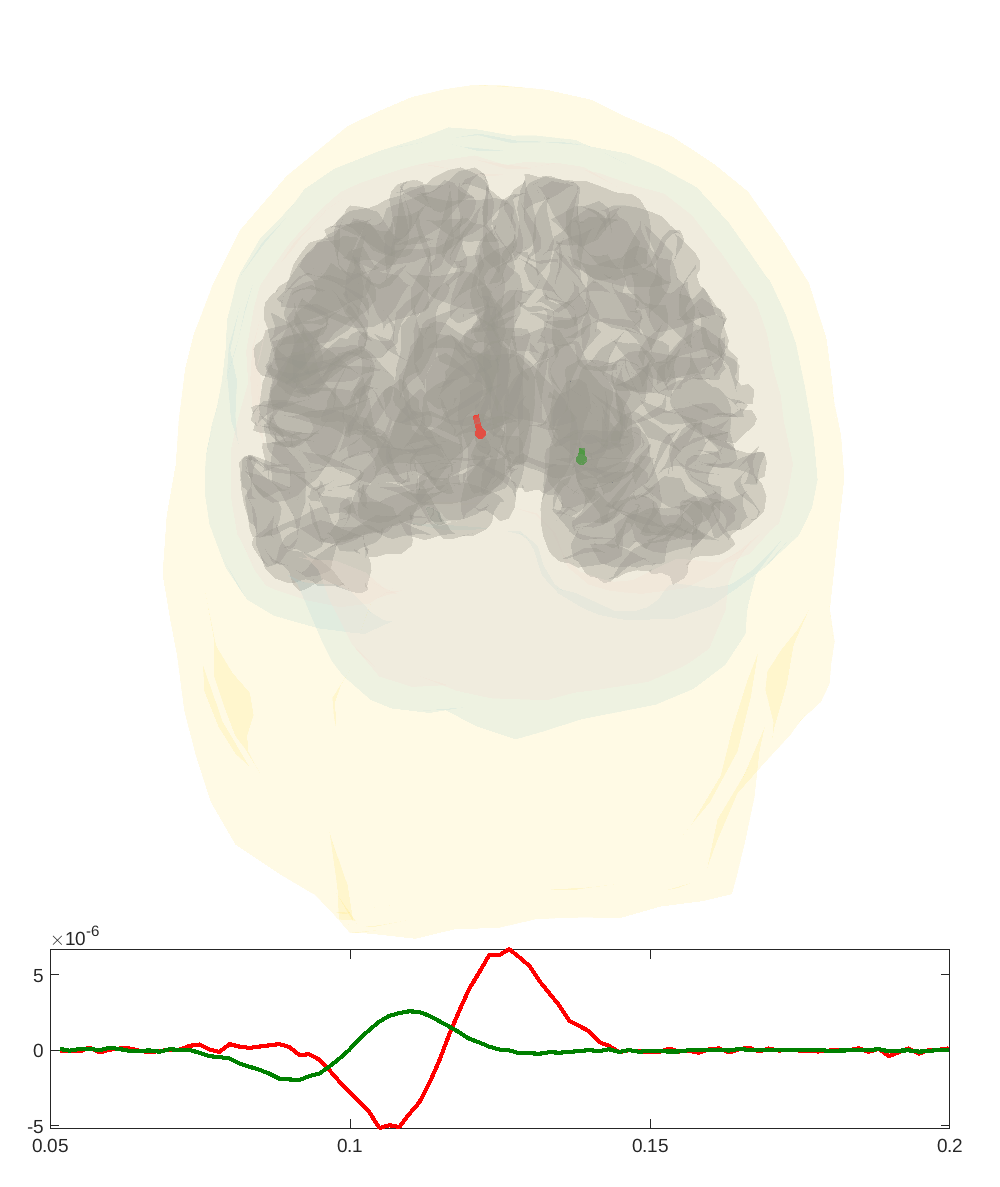
Note that FS3D takes as inputs actual EEG measurements, like time signals, and performs a suitable singular value decomposition in order to separate independent sources.

It appears that, in the rational approximation step, multiple poles possess a nice behavior with respect to branched singularities. This is due to the very physical assumptions on the model from dipolar current sources: for EEG data that correspond to measurements of the electrical potential, one should consider triple poles; this will also be the case for MEG – magneto-encephalography – data. However, for (magnetic) field data produced by magnetic dipolar sources, like in Section 6.1.2, one should consider poles of order five. Though numerically observed in 9, there is no mathematical justification so far why multiple poles generate such strong accumulation of the poles of the approximants. This intriguing property, however, is definitely helping source recovery and will be the topic of further study. It is used in order to automatically estimate the “most plausible” number of sources (numerically: up to 3, at the moment).

We studied the uniqueness of the critical point of the quadratic criterion in the electroencephalography problem for a single dipole situation (PhD of P. Asensio). This issue is essential for the use of descent algorithms. This leads to the study of the following criterion:

where $X$ and $X_0$ (actual dipole position) are in a smooth open set $\Omega$ included in ${ℝ}^3$ and $p$, $p_0$ (actual dipole moment) belong to ${ℝ}^3$. In the half-space case where $\Omega =\{(x,y,z)\in {ℝ}^3,z<0\}$, we have proven that there is a unique critical point.

For the spherical case where $\Omega =𝔹$ is the ball of center 0 and radius 1, we only obtained partial results so far, and managed to prove the uniqueness of the critical point in the specific case where $X_0=0$ is located at the center of ${\Omega }_0$.

We started considering a different class of models, not necessarily dipolar, and related estimation algorithms. Such models may be supported on the surface of the cortex or in the volume of the encephalon. We represent sources by vector-valued measures, and in order to favor sparsity in this infinite-dimensional setting we use a TV (i.e. total variation) regularization term as in Section 6.1.1. The approach follows that of 8 and is implemented through two different algorithms, whose convergence properties are currently being studied. Tests on synthetic data from a few dipolar sources provide results of different qualities that need to be better understood. In particular, a weight is being added in the TV term in order to better identify deep sources. This is the topic of the PhD researches of P. Asensio and M. Nemaire. Ultimately, the results will be compared to those of FS3D and other available software tools.

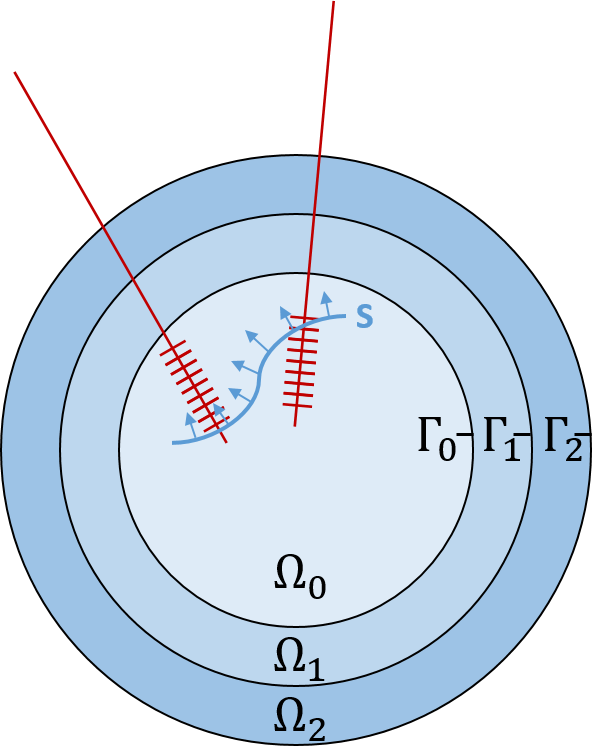
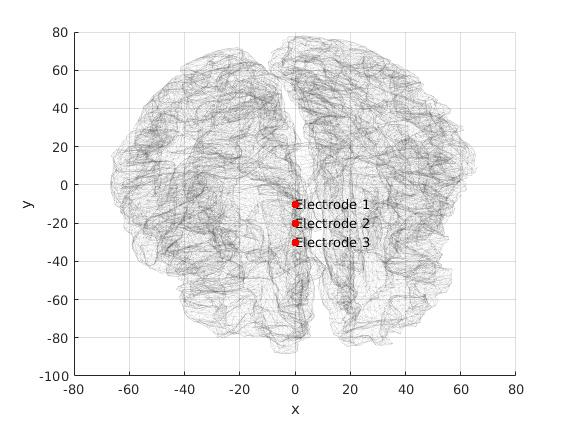
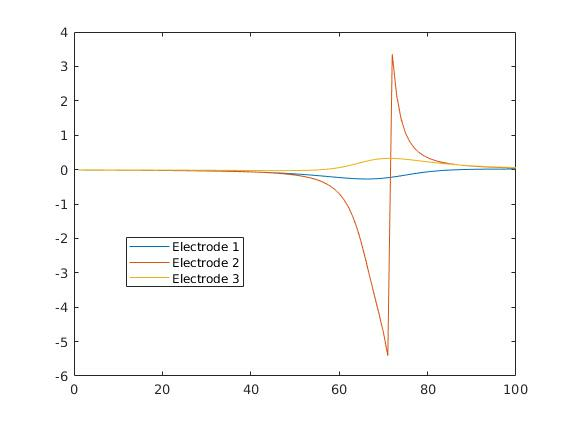
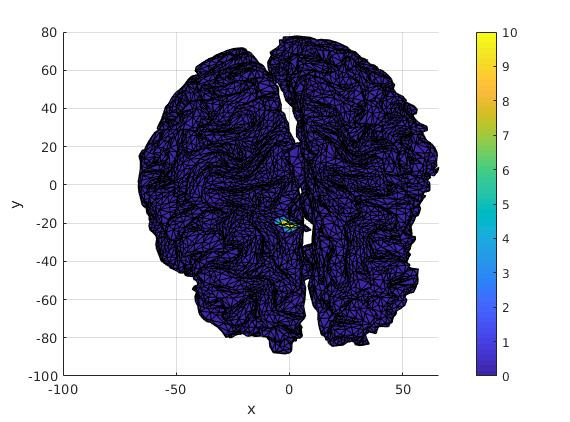
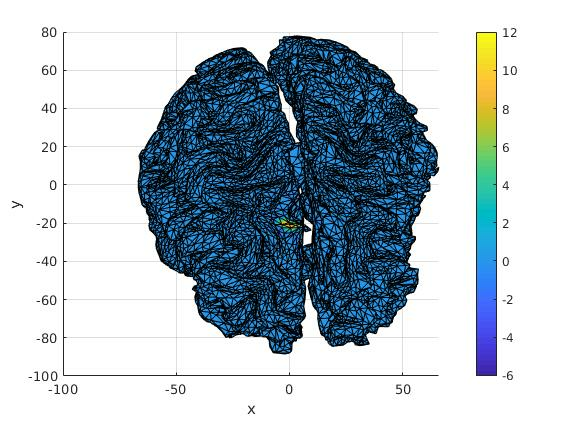
Progresses were made on the inverse problem of “Stereo” EEG (SEEG), where the potential is measured by deep electrodes and sensors within the brain as in the scheme of Figure 6. Assuming that the current source term $\mu$ is a ${ℝ}^3$-valued vector field (or a measure, or a dipolar distribution) supported on a surface $S$ and normally oriented to $S$, makes it possible to describe the potential $\varphi \left(\mu \right)$ generated by $\mu$ as a double layer potential:

The associated forward and inverse problems were solved for both an infinite medium conductor and a more realistic single model of the brain ${\Omega }_0$ (as first step towards nested domains for the head). Concerning the latter, it is preliminary assumed that $S\subset \partial {\Omega }_0$, whence $\mu$ consists in patches on the cortex surface.

The numerical implementation was done by approximating the density $\mu$ of the double layer potential with linear shape functions on triangulations of the involved surface $S$. For the discretized version, $\mu$ is then approximated on every triangle by a piecewise linear function, and the associated moment is taken to be located at the center of the triangle, perpendicular to the triangle. Note that explicit expressions of the double layer potential are also available at points located on $S$ (that supports $\mu$).

The inverse problem for SEEG is ill-posed and a Tikhonov regularization is used in order to solve the problem: find a distribution $\mu$ defined on the prescribed surface $S$ such that $\parallel \varphi \left(\mu \right)-{\varphi }^d{\parallel }_{L^2\left({\Omega }_0\right)}+\lambda R\left(\mu \right)$ is minimized, where ${\varphi }^d$ is the given data in ${\Omega }_0$, $\varphi \left(\mu \right)$ is the “forward model” (measurements of the double layer potential), $R\left(\mu \right)$ is an appropriate regularization term that results in $\mu$ having some desired properties (being bounded in $L^2$ norm or $TV$ or $L^1$ on $S$), and $\lambda$ a (Lagrange) parameter. Because ${\varphi }^d$ is only furnished at sensor positions, the $L^2$ term in the above criterion becomes an $l^2$ term. Figures 7 and 8 show the obtained results.

A further step will by to consider $S\subset {\Omega }_0$ within the brain, at the gray / white matters interface. Another one will be to add outer layers ${\Omega }_1$ and ${\Omega }_2$ for the skull and the scalp, as illustrated in Figure 6 in a spherical setup. Such configurations involve a data transmission / “cortical mapping” step, that relates the potential and normal current values at the boundaries ${\Gamma }_i$, that the present double layer formulation allows to solve with the source localization issue.

We are left to do further testing with real data and couple them data with simultaneous EEG / MEG data.

6.2 Matching problems and their applications: Finite degree bounds

Participants: Laurent Baratchart, Martine Olivi, Gibin Bose, David Martinez Martinez, Fabien Seyfert.

On the topic of uniform matching, Gibin Bose defended his thesis «Approximation $H^{\infty }$, Interpolation Analytique et Optimisation Convexe : Application à l’Adaptation d’Impédance Large Bande» on January 8th 2021. Triggered by remarks of one of the reviewers the PUMA code was extended to treat the presence of one transmission zero at infinity in the antenna's response and compare results obtained by our code with the classical Fano bound.

The Fano bound is very popular in the antenna community because of its simplicity. Under the realistic hypothesis that the load is totally reflective at high frequency, it states that: if $L_{11}$ is the reflection coefficient of the load, and $S_{11}$ the reflection coefficient of the global system (i.e. Matching Circuit + Load), then:

holds. Here $An{g}_{\infty }(.)$ stays for the angular derivative at infinity and $K=20\pi /log\left(10\right)$ is a constant. In other words the log modulus integral of the global system is bounded by the angular derivative of the load. Eventually, if we assume ideally that the global system's response is a step function centered on the pass-band $B$ (which is only possible with an infinite dimensional matching circuit), we get the following bound on the maximal matching log-level $R_L$ of the global system:

where $\left|B\right|$ stands for the length of the pass-band. $F_B$ is called the Fano bound, called after the name of its inventor, Fano, a PhD student of Bode. For a single resonance load, this band is sharp, provided an infinite dimensional matching circuit is at hand. For more complex loads, the Fano bound might be utterly optimistic.

We treated extensively the case of an antenna with a reflection coefficient of degree 3. On Figure 9 an absolute bound for a degree 2 matching circuit has been computed, leading to the depicted reflection coefficient $S_{22}$ yielding a matching level of $9.07\text{dB}$ in the prescribed band. This must be compared here to the $25.92\text{dB}$ of the Fano bound, which appears to be largely over optimistic. This discrepancy between the theoretical Fano bound and the bound computed by our method has two reasons. The antenna is of degree 3 and has in addition to its zero at infinity two additional finite transmission zeros. This deviation from a single resonance behavior is not taken into account by the classical Fano bound. Secondly as already mentioned the Fano bound supposes implicitly a step function shape of the system's response that can hardly be achieved in practice with a finite degree matching circuit. This underlines the necessity to obtain accurate finite degree bounds, as the ones obtained by the Puma software. These render effective a convex relaxation of the finite degree matching problem based on non-linear semi-definite programming and the notion of Pick matrix. A publication on this topic is under way.

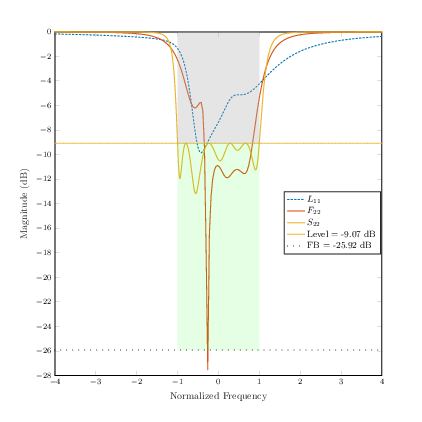
6.3 Modular filter synthesis with dispersive elements

Participants: Smain Amari, Martine Olivi, Fabien Seyfert.

This work was pursued in collaboration with Ke-L. Wu and Yan Zhang of the Chinese University of Hong-Kong.

In microwave filter synthesis the dispersive nature of couplings between resonators is usually neglected, due to the narrow band hypothesis. We however showed with S.Amari in 2008  28, 27 that a linear dependency in frequency of the couplings could be added to the usual state space model up to the addition of descriptor form, and that filter synthesis was still possible for simple inline topologies. We showed at that time that, if properly controlled, dispersion could be used to enrich the designer possibilities and lead to more selective filter responses by generation of additional transmission zeros.

This year we developed a completely new filter synthesis for cascaded topologies. The method starts with a functional bloc decomposition of the overall $2\times 2$ filter response to be realized. Each bloc is determined by a set of transmission zeros it is supposed to realize and the overall bloc decomposition corresponds therefore to a partition of the set of transmission zeros. It is only in a second step that each block is realized as a circuit. The cascading of all the so obtained circuits then yield the desired coupled resonator circuit. The procedure can be seen as combination of the Darlington synthesis and a structured realization procedure “à la” Ho-Kalman. The decomposition is brought into accordance with the cascaded topology to be realized thanks to the notion of angular derivative, that allows to relate the splitting in two parts of a resonator with the execution of a partial tangential Schur recurrence on the functional side. This has been the missing piece for decades in filter synthesis. Building up on this procedure, we showed that the circuital synthesis of elementary building blocks containing dispersive coupling is equivalent to a generalized Gramm-Schmidt orthogonalization process with two inner products involved. The overall procedure allows therefore for a very flexible modular synthesis, where each functional block can be implemented according to different techniques: in particular blocs including dispersive elements can be combined with classical triplets and quadruplets or inline sections. An order 6 filter, with 4 transmission zeros, was designed and implemented in combline technology using a capacitive-inductive coupling mechanism to realize dispersive couplings, see Figures 10, 11. The manufacturing took place at the Hong-Kong lab and underlines the complementarity of this collaboration that we aim to pursue.

The modular and dispersive synthesis method has been added prototypically to the software toolbox Dedale-HF Pro. Extensive tests are ahead of us before full integration of this new functionalities.

6.4 Stability assessment of microwave circuits

Participants: Laurent Baratchart, Sylvain Chevillard, Martine Olivi, Fabien Seyfert, Sébastien Fueyo, Adam Cooman.

The goal is here to help design amplifiers and oscillators, in particular to detect instability at an early stage of the design. This topic has been the subject of the PhD of S. Fueyo who defended this year. He was co-advised by L. Baratchart and J.-B. Pomet (from the McTao Inria project-team). Application to oscillator design methodologies is studied in collaboration with Smain Amari from the Royal Military College of Canada (Kingston, Canada).

As opposed to Filters and Antennas, Amplifiers and Oscillators are active components that intrinsically entail a non-linear functioning. The latter is due to the use of transistors governed by electric laws exhibiting saturation effects, and therefore inducing input/output characteristics that are no longer proportional to the magnitude of the input signal. Hence, they typically produce non-linear distortions. A central issue arising in the design of amplifiers is to assess stability. The latter may be understood around a functioning point when no input but noise is considered, or else around a periodic trajectory when an input signal at a specified frequency is applied. For oscillators, a precise estimation of their oscillating frequency is crucial during the design process. For devices operating at relatively low frequencies, time domain simulations perform satisfactorily to check stability. For complex microwave amplifiers and oscillators, the situation is however drastically different: the time step necessary to integrate the transmission line's dynamical equations (which behave like a simple electrical wire at low frequency) becomes so small that simulations are intractable in reasonable time. Moreover, most linear components of such circuits are known through their frequency response, and a preliminary, numerically unstable step is then needed to obtain their impulse response, prior to any time domain simulation.

For these reasons, the analysis of such systems is carried out in the frequency domain. To study stability around a functioning point, small input signals are considered and the stability of the linearized system can be investigated, using a first order approximation of each non-linear component, via the transfer impedance functions computed at certain ports of the circuit. In recent years, we showed that under realistic dissipativity assumptions at high frequency for the building blocks of the circuit, these transfer functions are meromorphic in the complex frequency variable $s$, with at most finitely many unstable poles in the right half-plane 3. Dwelling on the unstable/stable decomposition in Hardy Spaces, we developed a procedure to assess the stability or instability of the transfer functions at hand, from their evaluation on a finite frequency grid 11, that was further improved in 10 to address the design of oscillators, in collaboration with Smain Amari. This has resulted in the development of a software library called Pisa (see Section 3.4.1, aiming at making these techniques available to practitioners. Research in this direction now focuses on the links between the width of the measurement band, the density of the measurement points, and the precision with which an unstable pole, located within a certain depth into the complex plane, can be identified.

Extensions of the procedure to the strong signal case, where linearisation is considered around a periodic trajectory, have received attention over the last three years. When stability is studied around a periodic trajectory, determined in practice by Harmonic Balance algorithms, linearization yields a linear time varying dynamical system with periodic coefficients and a periodic trajectory thereof. While in finite dimension the stability of such systems is well understood via the Floquet theory, this is no longer the case in the present setting which is infinite dimensional, due to the presence of delays. Dwelling on known constructions for delay systems and on realization theory, using also some spectral theory and resolvents for Volterra equations, S. Fueyo's shows in his PhD thesis 20 that, for general circuits, the monodromy operator of the linearized system along its periodic trajectory is a compact perturbation of a delay system which is stable under a (realistic) assumption of passivity of components in the circuit at very high frequency. Thus, only finitely many unstable points can arise in the spectrum of the monodromy operator, and the latter is but the exponential of the singularities of the harmonic transfer function, viewed as a holomorphic function with values in periodic $L^2$ functions. This shows that the system is unstable if and only if the harmonic transfer function has poles in the right half plane, and these must lie equally spaced on finitely many vertical lines in that half plane. It is noteworthy that, in general, singularities of the harmonic transfer function are not necessarily singularities of the Fourier coefficients of the target $L^2$-function (the Fourier series can diverge even if all coefficients are very smooth), which is a completely new phenomenon that does not occur for finite-dimensional systems. However, in the case of polar singularities, at least one of these Fourier coefficients must have a pole. But since harmonic balance techniques can only estimate finitely many Fourier coefficients, one is not guaranteed to get a singular holomorphic function among them in the neighborhood of the pole under examination. This issue was apparently never considered by practitioners.

We published an article reporting about the stability of the high frequency system, and recast this result in terms of exponential stability of certain delay systems 14. We are also writing up a manuscript establishing the connections between the spectrum of the monodromy operator and the singularities of the harmonic transfer function, that may be seen as a generalization to the case of periodic coefficients of the well-known Henry-Hale theorem.

6.5 Hardy-Hodge decomposition with applications to silent sources

Participants: Laurent Baratchart, Juliette Leblond, Masimba Nemaire.

In a joint work with T. Qian and P. Dang from the university of Macao, we have proven that on a compact hypersurface $\Sigma$ embedded in ${ℝ}^n$, a ${ℝ}^n$-valued vector field of $L^p$ class decomposes as the sum of a harmonic gradient from inside $\Sigma$, a harmonic gradient from outside $\Sigma$, and a tangent divergence-free field, provided that $2-\epsilon <p<2+{\epsilon }^{\text{'}}$, where $\epsilon$ and ${\epsilon }^{\text{'}}$ depend on the Lipschitz constant of the surface. We also showed that the decomposition is valid for $1<p<\infty$ when $\Sigma$ is $VMO$-smooth (i.e.$\Sigma$ is locally the graph of Lipschitz function with derivatives in $VMO$). These result have been expounded in 23. By projection onto the tangent space, this gives us a Helmholtz-Hodge decomposition for vector fields on a compact Lipschitz hypersurface, which is apparently new since existing results deal with smooth surfaces. In fact, the Helmholtz-Hodge decomposition holds on Lipschitz surfaces (not just hypersurfaces),

In 22, we have showed that $L^p$-magnetizations (i.e. ${ℝ}^n$-valued vector fields) on a compact connected Lipschitz surface embedded in ${ℝ}^n$ that are silent outside (i.e. that produce no magnetic field in the unbounded component of the complement of the surface) form the orthogonal space (for the $L^p$-$L^q$ duality) to harmonic gradients inside the surface. This result teams up with the Hardy-Hodge decomposition to produce a description of silent magnetizations distributions of $L^p$-class on a surface as solution to a certain spectral equation for the double layer potential (for restricted range of $p$ when the surface is only Lipschitz). This last piece of research has been a collaboration with C. Gerhards and A. Kegeles from TU Freiberg. It can be used use to characterize, via balayage, silent magnetizations in a volume rather than on a surface.

Besides, we have also been working on a direct characterization of silent ${\left[L^p\left(\Omega \right)\right]}^n$, ($n\ge 3$) vector-fields in a volume. We showed that a vector field carried by some open set $\Omega$ with boundary of measure zero is silent if and only if, in its Helmholtz decomposition as the sum of a $L^p$ gradient and a divergence-free $L^p$ field over ${ℝ}^n$, both summands vanish a.e. outside of $\Omega$. When $\Omega$ is Lipschitz, this entails that silent vector-fields $M\in {\left[L^p\left(\Omega \right)\right]}^n$ (i.e. vector fields representing magnetizations that produce the zero magnetic field outside $\Omega$) are of the form $M=\nabla \psi +D$ with $\psi \in W_0^{1,p}\left(\Omega \right)$ (the familiar space of Sobolev functions with zero trace) and $D$ divergence-free with zero normal normal component on the boundary $\partial \Omega$. It should be notice that this fact holds for $1<p<\infty$, even though the Helmholtz decomposition on $\Omega$ may not hold for every $L^p$-field (in general it only holds for $p$ in a neighborhood of $[2/3,3]$). The previous characterization makes it possible to describe the norm-minimizing equivalent vector-field to a given vector-field $M\in {\left[L^p\left(\Omega \right)\right]}^n$. Here, two vector-fields are equivalent if their magnetic potentials outside $\Omega$ differ by a constant, or equivalently if the vector-fields differ by a silent source. We explicitly characterized the norm-minimizing equivalent source when $p=2$ in terms of the solution to a Dirichlet problem for the Laplacian in $\Omega$, but when $p\ne 2$ one faces a $p$-Dirac equation whose boundary conditions are not as explicit. This is tantamount to compute a nonlinear generalization of the Helmholtz-Hodge decomposition (which exists for all $p$) where the harmonic gradient term gets replaced by a $p$-harmonic term. Alternatively, the characterization can be achieved via a dual maximization problem.

6.6 Identification of resonating frequencies of compact metallic objects in electromagnetic inverse scattering

Participants: Laurent Baratchart, Juliette Leblond, Martine Olivi, Fabien Seyfert.

We started an academic collaboration with LEAT (Univ. Côte d'Azur, France, people. involved: Jean-Yves Dauvignac, Nicolas Fortino, Yasmina Zaki) on the topic of inverse scattering using frequency dependent measurements. As opposed to classical electromagnetic imaging where several spatially located sensors are used to identify the shape of an object by means of scattering data at a single frequency, a discrimination process between different metallic objects is here being sought for by means of a single, or a reduced number of sensors that operate on a whole frequency band. For short the spatial multiplicity and complexity of antenna sensors is here traded against a simpler architecture performing a frequency sweep.

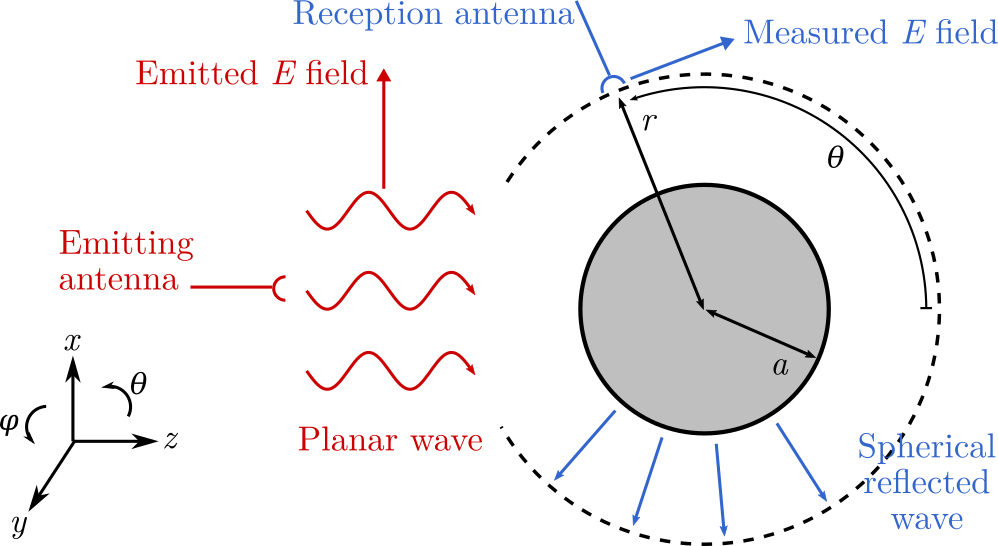
The setting is shown on Figure 12. The total field $E_t(r,\theta ,\varphi )$ is the sum of the incident field $E_i$ (here a plane wave) and scattered field $E_s$, that is at every point in space we have $E_t=E_i+E_s$. A harmonic time dependency ($e^{j\omega t}$, where $j$ is the imaginary unit: $j^2=-1$ ) is supposed for the incident wave, so that by linearity of Maxwell equations and after a transient state, following holds,

The subscripts $o$ and $e$ stand here for «observation point» and «emission point»: the scattered field at the observation point is therefore related to the emitted planar wave field at the emission point via the transfer function $H(s=j\omega ,{\theta }_o,{\varphi }_o)$. The emission point is here supposed fixed, so the dependency in $e$ is omitted in $H$. Under regularity conditions on the scatterer's boundary the function $H$ can be shown to admit an analytic continuation into the complex left half plane for the $s$ variable, away from a discrete set (with a possible accumulation point a infinity) where it admits poles. Thus, $H$ is a meromorphic function in the variable $s$. Its poles are called the resonating frequencies of the scattering object. Recovering these resonating frequencies from frequency scattering measurement, that is measurements of $H$ at particular $s=j{\omega }_i^{\text{'}}s$ is the primary objective of this project.

In order to gain some insight we started a full study of the particular case when the scatterer is a spherical PEC (Perfectly Electric Conductor). In this case Maxwell equations can be solved «explicitly» by means of expansions in series of vectorial spherical harmonics. We showed in particular that in this case $H$ admits following simple structure:

where $R$ is a meromorphic functions with poles at zeros of the spherical Hankel functions and their derivatives and $C$ is independent of the frequency. Identification procedures, surprisingly close to the ones we developed in connection with amplifier stability analysis, are currently being studied to gain information about the resonating frequencies by means of a rational approximation of the function $R$ once it has been de-embedded. A preliminary study resulted in a common publication with the LEAT team 18. Generalization of this analysis and procedure will be considered for arbitrarily compact PEC objects.

6.7 Imaging and modeling ancient materials

Participants: Vanna Lisa Coli, Kassem Dia, Juliette Leblond.

This is a recent activity of the team, linked to image classification in archaeology in the framework of the projects ToMaT and Arch-AI-Story (see Section 8.5) and to the post-doctoral stay of V. L. Coli; it is pursued in collaboration with L. Blanc-Féraud (project-team Morpheme, I3S-CNRS/Inria Sophia/iBV), D. Binder (CEPAM-CNRS, Nice), in particular.

The pottery style is classically used as the main cultural marker within Neolithic studies. Archaeological analyses focus on pottery technology, and particularly on the first stages of pottery manufacturing processes. These stages are the most demonstrative for identifying the technical traditions, as they are considered as crucial in apprenticeship processes. Until now, the identification of pottery manufacturing methods was based on macro-traces analysis, i.e. surface topography, breaks and discontinuities indicating the type of elements (coils, slabs, ...) and the way they were put together for building the pots. Overcoming the limitations inherent to the macroscopic pottery examination requires a complete access to the internal structure of the pots. Micro-computed tomography ($\mu$CT) has recently been used for exploring ancient materials micro-structure. This non-invasive method provides quantitative data for a big set of proxies and is perfectly adapted to the analysis of Cultural heritage materials.

The main challenge of our current analyses aims to overcome the lack of existing protocols to apply in order to quantify observations. In order to characterize the manufacturing sequences, the mapping of the paste variability (distribution and composition of temper) and the discontinuities linked to different classes of pores, fabrics and/or organic inclusions appears promising. The totality of the acquired images composes a set of 2-D and 3-D surface and volume data at different resolutions and with specific physical characteristics related to each acquisition modality (multimodal and multi-scale data). Specific shape recognition methods need to be developed by application of robust imaging techniques and 3-D-shapes recognition algorithms.

In a first step, we devised a method to isolate pores from the 3-D data volumes in binary 3-D images, to which we apply a process named Hough transform (derived from Radon transform). This method, of which the generalization from 2-D to 3-D is quite recent, allows us to evaluate the presence of parallel lines going through the pores. The quantity of such lines and their parallelism furnish good indicators of the “coiling” manufacturing, that they allow to distinguish from the other “spiral patchwork” technique, in particular. These progresses are described in an article submitted for publication4.

Other possibilities of investigation are being analyzed as well, such as machine learning and deep learning techniques. Encouraging classification results were obtained5.

7.1 Bilateral Contracts with Industry

8.1 International Initiatives

8.2 International Research Visitors

8.3 European Initiatives

8.4 National Initiatives

8.5 Regional Initiatives

8.6 List of international and industrial partners

Figure 13 sums up who are our main collaborators, users and competitors.

9.1 Promoting Scientific Activities

9.2 Teaching - Supervision - Juries

9.3 Popularization

10.1 Major publications

• 1 articleSmainS. Amari, FabienF. Seyfert and M. Bekheit. Theory of Coupled Resonator Microwave Bandpass Filters of Arbitrary BandwidthMicrowave Theory and Techniques, IEEE Transactions on588August 2010, 2188--2203
  back to text
• 2 articleBilalB. Atfeh, LaurentL. Baratchart, JulietteJ. Leblond and Jonathan R.J. Partington. Bounded extremal and Cauchy-Laplace problems on the sphere and shellJ. Fourier Anal. Appl.162Published online Nov. 20092010, 177--203URL: http://dx.doi.org/10.1007/s00041-009-9110-0
  back to textback to textback to text
• 3 unpublishedLaurentL. Baratchart, SylvainS. Chevillard, AdamA. Cooman, MartineM. Olivi and FabienF. Seyfert. Linearized Active Circuits: Transfer Functions and StabilityDecember 2018, working paper or preprint
  HALback to text
• 4 articleLaurentL. Baratchart, SylvainS. Chevillard and TaoT. Qian. Minimax principle and lower bounds in $H^2$-rational approximation'Journal of Approximation Theory2062015, 17--47
  back to text
• 5 articleLaurentL. Baratchart, JulietteJ. Leblond, StéphaneS. Rigat and EmmanuelE. Russ. Hardy spaces of the conjugate Beltrami equationJournal of Functional Analysis25922010, 384-427URL: http://dx.doi.org/10.1016/j.jfa.2010.04.004
  back to textback to text
• 6 article LaurentL. Baratchart, MartineM. Olivi and FabienF. Seyfert. Boundary nevanlinna-pick interpolation with prescribed peak points. Application to impedance matching SIAM Journal on Mathematical Analysis 2017
  HAL DOI
• 7 articleLaurentL. Baratchart, HerbertH. Stahl and MaximM. Yattselev. Weighted Extremal Domains and Best Rational ApproximationAdvances in Mathematics2292012, 357-407URL: http://hal.inria.fr/hal-00665834
  back to textback to textback to textback to text
• 8 article LaurentL. Baratchart, CristobalC. Villalobos Guillén, DougD. Hardin, MichaelM. Northington and EdwardE. Saff. Inverse Potential Problems for Divergence of Measures with Total Variation Regularization Foundations of Computational Mathematics November 2019
  HAL DOI back to text
• 9 articleMaureenM. Clerc, JulietteJ. Leblond, Jean-PaulJ.-P. Marmorat and ThéodoreT. Papadopoulo. Source localization using rational approximation on plane sectionsInverse Problems285May 2012, 24URL: http://hal.inria.fr/inria-00613644
  back to textback to textback to textback to text
• 10 inproceedings AdamA. Cooman, FabienF. Seyfert and SmainS. Amari. Estimating unstable poles in simulations of microwave circuits IMS 2018 Philadelphia, United States June 2018
  HAL back to text
• 11 article AdamA. Cooman, FabienF. Seyfert, MartineM. Olivi, SylvainS. Chevillard and LaurentL. Baratchart. Model-Free Closed-Loop Stability Analysis: A Linear Functional Approach IEEE Transactions on Microwave Theory and Techniques https://arxiv.org/abs/1610.03235 2017
  HAL back to text
• 12 articleMartineM. Olivi, FabienF. Seyfert and Jean-PaulJ.-P. Marmorat. Identification of microwave filters by analytic and rational H2 approximationAutomatica492January 2013, 317-325URL: http://hal.inria.fr/hal-00753824
  DOIback to textback to text
• 13 articleYanY. Zhang, FabienF. Seyfert, SmainS. Amari, MartinM. Olivi and KE-LiK.-L. Wu. General Synthesis Method for Dispersively Coupled Resonator Filters With Cascaded TopologiesIEEE Transactions on Microwave Theory and TechniquesDecember 2020, 15
  HALDOI

10.2 Publications of the year

10.3 Cited publications

• 25 book N.~I.N. Achieser. Elements of the Theory of Elliptic Functions AMS 1990
  back to text
• 26 articleD. Alpay, LaurentL. Baratchart and AndreaA. Gombani. On the Differential Structure of Matrix-Valued Rational Inner FunctionsOperator Theory~: Advances and Applications731994, 30--66
  back to textback to textback to text
• 27 inproceedingsS. Amari, M. Bekheit and F. Seyfert. Notes on Bandpass Filters Whose Inter-Resonator Coupling Coefficients Are Linear Functions of Frequency2008 IEEE MTT-S International Microwave Symposium DigestJune 2008, 1207-1210
  DOIback to text
• 28 articleSmainS. Amari, FabienF. Seyfert and M. Bekheit. Theory of Coupled Resonator Microwave Bandpass Filters of Arbitrary BandwidthIEEE Transactions on Microwave Theory and Techniques5882010, 2188 -2203
  HALDOIback to text
• 29 book J.~A.J. Ball, I. Gohberg and L. Rodman. Interpolation of rational matrix functions Birkhäuser 1990
  back to text
• 30 articleLaurentL. Baratchart. A remark on uniqueness of best rational approximants of degree 1 in $L^2$ of the circle' Elec. Trans.on Numerical Anal.252006, 54--66
  back to text
• 31 article LaurentL. Baratchart, AlexandreA. Borichev and SlahS. Chaabi. Pseudo-holomorphic functions at the critical exponent Journal of the European Mathematical Society 18 9 2016
  HAL DOI back to text back to text
• 32 article LaurentL. Baratchart, LaurentL. Bourgeois and JulietteJ. Leblond. Uniqueness results for inverse Robin problems with bounded coefficient Journal of Functional Analysis 2016
  HAL DOI back to text back to text
• 33 articleLaurentL. Baratchart, M. Cardelli and MartineM. Olivi. Identification and rational $L^2$ approximation: a gradient algorithm'Automatica271991, 413--418
  back to textback to text
• 34 articleLaurentL. Baratchart, M. Chyba and Jean-BaptisteJ.-B. Pomet. A Grobman-Hartman theorem for control systemsJ. Dyn. Differential Eqs.192007, 75-107
  back to text
• 35 articleLaurentL. Baratchart, YannickY. Fischer and JulietteJ. Leblond. Dirichlet/Neumann problems and Hardy classes for the planar conductivity equationComplex Variables and Elliptic Equations2014, 41
  HALDOIback to textback to text
• 36 inproceedings LaurentL. Baratchart, L. Golinskii and StanislasS. Kupin. Orthogonal rational functions and nonstationary stochastic processes: a Szegő theory Proc. 19th Symposium on Mathematical Theory of Networks and Systems Budapest 2010
  back to text
• 37 articleLaurentL. Baratchart, Douglas P.D. Hardin, Eduardo AndradeE. Lima, Edward~B.E. Saff and BenjaminB. Weiss. Characterizing kernels of operators related to thin-plate magnetizations via generalizations of Hodge decompositionsInverse Problems2912013, URL: https://hal.inria.fr/hal-00919261
  DOIback to textback to textback to text
• 38 articleLaurentL. Baratchart, ReinholdR. Kuestner and VilmosV. Totik. Zero distributions via orthogonalityAnnales de l'Institut Fourier5552005, 1455--1499
  back to textback to text
• 39 articleLaurentL. Baratchart, StanislasS. Kupin, VincentV. Lunot and MartineM. Olivi. Multipoint Schur algorithm and orthogonal rational functions: convergence properties, IJournal d'Analyse1122011, 207-255URL: https://arxiv.org/abs/0812.2050v3
  back to text
• 40 articleLaurentL. Baratchart and JulietteJ. Leblond. Hardy approximation to $L^p$ functions on subsets of the circle with $1p<$'Constructive Approximation141998, 41--56
  back to textback to text
• 41 articleLaurentL. Baratchart, JulietteJ. Leblond, FrédéricF. Mandréa and Edward~B.E. Saff. How can meromorphic approximation help to solve some 2D inverse problems for the Laplacian?Inverse Problems1511999, 79--90URL: https://dx.doi.org/10.1088/0266-5611/15/1/012
  back to textback to textback to text
• 42 articleLaurentL. Baratchart, JulietteJ. Leblond and Jean-PaulJ.-P. Marmorat. Sources identification in 3D balls using meromorphic approximation in 2D disksElectronic Transactions on Numerical Analysis (ETNA)252006, 41--53
  back to textback to textback to text
• 43 articleLaurentL. Baratchart, JulietteJ. Leblond and Jonathan~R.J. Partington. Hardy approximation to $L^{}$ functions on subsets of the circle'Constructive Approximation121996, 423--435
  back to text
• 44 articleLaurentL. Baratchart, JulietteJ. Leblond and FabienF. Seyfert. Constrained extremal problems in H2 and Carleman's formulasMatematicheskii Sbornik20972018, 36
  HALback to text
• 45 articleLaurentL. Baratchart, FrédéricF. Mandréa, Edward~B.E. Saff and FranckF. Wielonsky. 2D inverse problems for the Laplacian: a meromorphic approximation approachJournal de Math. Pures et Appliquées862008, 1-41
  back to textback to textback to textback to text
• 46 articleLaurentL. Baratchart and MartineM. Olivi. Critical points and error rank in best $H^2$ matrix rational approximation of fixed McMillan degree'Constructive Approximation141998, 273--300
  back to text
• 47 articleLaurentL. Baratchart and MartineM. Olivi. Index of critical points in $l^2$-approximation'System and Control Letters101988, 167--174
  back to text
• 48 inproceedingsLaurentL. Baratchart. On the $H^2$ Rational Approximation of Markov Matrix-Valued Functions'Proc. 17th Symposium on Mathematical Theory of Networks and Systems (MTNS)Kyoto, Japon2006, 180--182
  back to text
• 49 articleLaurentL. Baratchart, Edward~B.E. Saff and FranckF. Wielonsky. A criterion for uniqueness of a critical point in $H^2$ rational approximation'Journal d'Analyse701996, 225--266
  back to text
• 50 articleLaurentL. Baratchart and FabienF. Seyfert. An $L^p$ analog to AAK theory for $p2$'Journal of Functional Analysis19112002, 52--122
  back to textback to text
• 51 articleLaurentL. Baratchart, HerbertH. Stahl and FranckF. Wielonsky. Asymptotic uniqueness of best rational approximants of given degree to Markov functions in $L^2$ of the circle'Constr. Approx.1712001, 103--138
  back to text
• 52 incollectionLaurentL. Baratchart and MaximM. Yattselev. Asymptotic uniqueness of best rational approximants to complex Cauchy transforms in $L^2$ of the circle'Recent trends in orthogonal polynomials and approximation theory507Contemp. Math.Providence, RIAmer. Math. Soc.2010, 87--111
  back to text
• 53 articleLaurentL. Baratchart and MaximM. Yattselev. Convergent Interpolation to Cauchy Integrals over Analytic Arcs with Jacobi-Type WeightsInternational Mathematics Research Notices2010222010, 4211--4275URL: https://hal.inria.fr/hal-00508314
  back to text
• 54 articleLaurentL. Baratchart and MaximM. Yattselev. Convergent interpolation to Cauchy integrals over analytic arcsFound. Comp. Math.962009, 675--715
  back to text
• 55 articleLaurentL. Baratchart and MaximM. Yattselev. Meromorphic approximants for complex Cauchy transforms with polar singularitiesMat. Sbornik20092009, 3-40
  back to text
• 56 articleAmelA. Ben~Abda, FehmiF. Ben~Hassen, JulietteJ. Leblond and MoncefM. Mahjoub. Sources recovery from boundary data: a model related to electroencephalographyMathematical and Computer Modelling4911--122009, 2213--2223URL: https://dx.doi.org/10.1016/j.mcm.2008.07.016
  back to textback to text
• 57 articleR.J.R. Cameron, Jean-CharlesJ.-C. Faugère, FabriceF. Rouillier and FabienF. Seyfert. Exhaustive approach to the coupling matrix synthesis problem and application to the design of high degree asymmetric filtersInternational Journal of RF and Microwave Computer-Aided Engineering1712007, 4--12URL: https://hal.inria.fr/hal-00663777
  back to text
• 58 articleR.J.R. Cameron, A.R.A. Harish and C.J.C. Radcliffe. Synthesis of advanced microwave filters without diagonal cross-couplingsIEEE Transactions on Microwave Theory and Techniques5012dec 2002, 2862--2872URL: https://dx.doi.org/10.1109/TMTT.2002.805141
  back to text
• 59 articleSlimS. Chaabane, I. Fellah, MohamedM. Jaoua and JulietteJ. Leblond. Logarithmic stability estimates for a Robin coefficient in 2D Laplace inverse problemsInverse Problems2012004, 49--57URL: https://dx.doi.org/10.1088/0266-5611/20/1/003
  back to text
• 60 phdthesis SlahS. Chaabi. Analyse complexe et problèmes de Dirichlet dans le plan : équation de Weinstein et autres conductivités non bornées Mathématiques et Informatique de Marseille 2013
  back to text
• 61 articleR.R.R. Coifman, R. Rochberg and G. Weiss. Factorization theorems for Hardy spaces in several variablesAnn. Math.1031976, 611--635
  back to text
• 62 phdthesisYannickY. Fischer. Approximation des des classes de fonctions analytiques généralisées et résolution de problèmes inverses pour les tokamaksUniv. Nice Sophia Antipolis2011, URL: https://tel.archives-ouvertes.fr/tel-00643239/
  back to textback to text
• 63 articleA. Friedman and M. Vogelius. Determining cracks by boundary measurementsIndiana Univ. Math. J.3831989, 527--556
  back to text
• 64 articleP. Fulcheri and MartineM. Olivi. Matrix rational $H^2$-approximation: a gradient algorithm based on Schur analysis'SIAM J. on Control & Optim.361998, 2103--2127
  back to text
• 65 book J.~B.J. Garnett. Bounded analytic functions Academic Press 1981
  back to text
• 66 articleT. Georgiou. A topological approach to Nevanlinna-Pick interpolationSIAM J. Math. Anal.1851987, 1248--1260
  back to text
• 67 articleBernardB. Hanzon, MartineM. Olivi and Ralf~L.M.R. Peeters. Balanced realizations of discrete-time stable all-pass systems and the tangential Schur algorithmLinear Algebra and its Applications4182006, 793-820URL: https://dx.doi.org/10.1016/j.laa.2006.09.029
  back to textback to textback to text
• 68 articleJ.W.J. Helton and D.E.D. Marshall. Frequency domain analysis and analytic selectionsIndiana Univ. Math. J.3911990, 157--184
  back to text
• 69 book TadeuszT. Iwaniec and GavenG. Martin. Geometric function theory and non-linear analysis Oxford Univ. Press 2001
  back to text
• 70 book N.S.N. Landkhof. Foundations of modern potential theory Springer-Verlag 1972
  back to text
• 71 book M.M.M. Lavrentiev. Some Improperly Posed Problems of Mathematical Physics Springer 1967
  back to text
• 72 articleVincentV. Lunot, FabienF. Seyfert, StéphaneS. Bila and A. Nasser. Certified Computation of Optimal Multiband Filtering FunctionsIEEE Transactions on Microwave Theory and Techniques5612008, 105-112URL: https://dx.doi.org/10.1109/TMTT.2007.912234
  back to textback to text
• 73 articleJean-PaulJ.-P. Marmorat and MartineM. Olivi. Nudelman Interpolation, Parametrization of Lossless Functions and balanced realizationsAutomatica432007, 1329--1338URL: https://dx.doi.org/10.1016/j.automatica.2007.01.020
  back to textback to textback to text
• 74 articleH. Orchard and G. Temes. Filter Design Using Transformed VariablesIEEE Transactions on Circuit Theory154dec 1968, 385--408URL: https://dx.doi.org/10.1109/TCT.1968.1082870
  back to text
• 75 book VladimirV. Peller. Hankel Operators and their Applications Springer 2003
  back to text back to text
• 76 articleA. Schneck. Constrained Hardy space approximationJ. Approx. Theory82010, 1466--1483
  back to text
• 77 articleI. Schur. Über Potenzreihen die im innern des einheitskreises beschränkt sindJ. Reine Angew. Math.1471917, 205--232
  back to text
• 78 inproceedingsFabienF. Seyfert, LaurentL. Baratchart, Jean-PaulJ.-P. Marmorat, StéphaneS. Bila and JacquesJ. Sombrin. Extraction of coupling parameters for microwave filters: determinati on of a stable rational model from scattering data2003 IEEE MTT-S International Microwave Symposium Digest1Philadelphie, États-UnisIEEE2003, 25--28URL: https://hal.inria.fr/hal-00663504
  back to text
• 79 articleS. Smirnov. Decomposition of solenoidal vector charges into elementary solenoids and the structure of normal one-dimensional currentsAlgebra i Analiz4Transl. St Petersburg Math. Journal, n. 4, pp. 841--867, 19941993, 206-238
  back to text
• 80 book E.~M.E. Stein. Harmonic Analysis Princeton University Press 1993
  back to text
• 81 book AlmudenaA. Suàrez and RaymondR. Quéré. Stability analysis of nonlinear microwave circuits Artech House 2003
  back to text
• 82 inproceedingsT. Wolff. Counterexamples with harmonic gradients in ${𝐑}^3$'Essays on Fourier analysis in honor of Elias M. Stein42Math. Ser.Princeton Univ. Press1995, 321--384
  back to text