2.1 Presentation

The general objective of the Toccata project is to promote formal specification and computer-assisted proof in the development of software that requires high assurance in terms of safety and correctness with respect to its intended behavior. Such safety-critical software appears in many application domains like transportation (e.g., aviation, aerospace, railway, and more and more in cars), communication (e.g., internet, smartphones), health devices, etc. The number of tasks performed by software is quickly increasing, together with the number of lines of code involved. Given the need of high assurance of safety in the functional behavior of such applications, the need for automated (i.e., computer-assisted) methods and techniques to bring guarantee of safety became a major challenge. In the past and at present, the most widely used approach to check safety of software is to apply heavy test campaigns, which take a large part of the costs of software development. Yet they cannot ensure that all the bugs are caught, and remaining bugs may have catastrophic causes (e.g., the Heartbleed bug in OpenSSL library discovered in 2014 https://en.wikipedia.org/wiki/Heartbleed).

Generally speaking, software verification approaches pursue three goals: (1) verification should be sound, in the sense that no bugs should be missed, (2) verification should not produce false alarms, or as few as possible, (3) it should be as automatic as possible. Reaching all three goals at the same time is a challenge. A large class of approaches emphasizes goals (2) and (3): testing, run-time verification, symbolic execution, model checking, etc. Static analysis, such as abstract interpretation, emphasizes goals (1) and (3). Deductive verification emphasizes (1) and (2). The Toccata project is mainly interested in exploring the deductive verification approach, although we also consider the other ones in some cases.

In the past decade, there have been significant progress made in the domain of deductive program verification. They are emphasized by some success stories of application of these techniques on industrial-scale software. For example, the Atelier B system was used to develop part of the embedded software of the Paris metro line 14  39 and other railway-related systems; a formally proved C compiler was developed using the Coq proof assistant  56; the L4-verified project developed a formally verified micro-kernel with high security guarantees, using analysis tools on top of the Isabelle/HOL proof assistant  55. A bug in the JDK implementation of TimSort was discovered using the KeY environment  62 and a fixed version was proved sound. Another sign of recent progress is the emergence of deductive verification competitions (e.g., VerifyThis 1). Finally, recent trends in the industrial practice for development of critical software is to require more and more guarantees of safety, e.g., the new DO-178C standard for developing avionics software adds to the former DO-178B the use of formal models and formal methods. It also emphasizes the need for certification of the analysis tools involved in the process.

Panorama of Deductive Verification

There are two main families of approaches for deductive verification. Methods in the first family build on top of mathematical proof assistants (e.g., Coq, Isabelle) in which both the model and the program are encoded; the proof that the program meets its specification is typically conducted in an interactive way using the underlying proof construction engine. Methods from the second family proceed by the design of standalone tools taking as input a program in a particular programming language (e.g., C, Java) specified with a dedicated annotation language (e.g., ACSL 36, JML 45) and automatically producing a set of mathematical formulas (the verification conditions) which are typically proved using automatic provers (e.g., Z3 63, Alt-Ergo 48, CVC4 35).

The first family of approaches usually offers a higher level of assurance than the second, but also demands more work to perform the proofs (because of their interactive nature) and makes them less easy to adopt by industry. Moreover, they generally do not allow to directly analyze a program written in a mainstream programming language like Java or C. The second kind of approaches has benefited in the past years from the tremendous progress made in SAT and SMT solving techniques, allowing more impact on industrial practices, but suffers from a lower level of trust: in all parts of the proof chain (the model of the input programming language, the VC generator, the back-end automatic prover), potential errors may appear, compromising the guarantee offered. Moreover, while these approaches are applied to mainstream languages, they usually support only a subset of their features.

Overall Goals of the Toccata Project

One of our original skills is the ability to conduct proofs by using automatic provers and proof assistants at the same time, depending on the difficulty of the program, and specifically the difficulty of each particular verification condition. We thus believe that we are in a good position to propose a bridge between the two families of approaches of deductive verification presented above. Establishing this bridge is one of the goals of the Toccata project: we want to provide methods and tools for deductive program verification that can offer both a high amount of proof automation and a high guarantee of validity. Indeed, an axis of research of Toccata is the development of languages, methods and tools that are themselves formally proved correct. Recent advances in the foundations of deductive verification include various aspects such as reasoning efficiently on bitvector programs 7 or providing counterexamples when a proof does not succeed 49.

A specifically challenging aspect of deductive verification methods is how one does deal with memory mutation in general, an issue that appear under various similar form such the reasoning on mutable data structures or on concurrent programs, with the common denominator of the tracking of memory change on shared data. The ability to track aliasing is also a key for the ability of specifying programs and conduct proofs using the advanced notion of ghost code6.

In industrial applications, numerical calculations are very common (e.g. control software in transportation). Typically they involve floating-point numbers. Some of the members of Toccata have an internationally recognized expertise on deductive program verification involving floating-point computations. Our past work includes a new approach for proving behavioral properties of numerical C programs using Frama-C/Jessie 34, various examples of applications of that approach 43, the use of the Gappa solver for proving numerical algorithms 61, an approach to take architectures and compilers into account when dealing with floating-point programs 44, 60. We contributed to the CompCert verified compiler, regarding the support for floating-point operations 2. We also contributed to the Handbook of Floating-Point Arithmetic 59. A representative case study is the analysis and the proof of both the method error and the rounding error of a numerical analysis program solving the one-dimension acoustic wave equation 4140. We published a reference book on the verification of floating-point algorithms with Coq 3. Our experience led us to a conclusion that verification of numerical programs can benefit a lot from combining automatic and interactive theorem proving 42, 43, 50. Verification of numerical programs is another main axis of Toccata.

Deductive program verification methods are built upon theorem provers to decide whether a expected proof obligation on a program is a valid mathematical proposition, hence working on deductive verification requires a certain amount of work on the aspect of design of theorem provers. We are involved in particular in the Alt-Ergo SMT solver, for which we designed an original approach for reasoning on arithmetic facts 510 ; and the Gappa tool dedicated to reasoning on rounding errors in floating-point computations 8. Proof by reflection is also a powerful approach for advanced reasoning about programs 9.

In the past, we have been more and more involved in the development of significantly large case studies and applications, such as for example the verification of matrix multiplication algorithms 4, the design of verified OCaml librairies 46, the realization of a platform for verification of shell scripts 37, or the correct-by-construction design of an efficient library for arbitrary-precision arithmetic 9.

Our scientific programme detailed below is structured into four axes:

1. Foundations and spreading of deductive program verification;
2. Reasoning on mutable memory in program verification;
3. Verification of Computer Arithmetic;
4. Spreading Formal Proofs.

Let us conclude with more general considerations about our agenda of the next four years: we want to keep on

• with general audience actions;
• industrial transfer, in particular through an extension of the perimeter of the ProofInUse joint lab.

3.1 Foundations and spreading of deductive program verification

Permanent researchers: S. Conchon, J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich

This axis covers the central theme of the team: deductive verification, from the point of view of its foundations but also our will to spread its use in software development. The general motto we want to defend is “deductive verification for the masses”. A non-exhaustive list of subjects we want to address is as follows.

• The verification of general-purpose algorithms and data structures: the challenge is to discover adequate invariants to obtain a proof, in the most automatic way as possible, in the continuation of the current VOCaL project and the various case studies presented in Axis 4 below.
• Uniform approaches to obtain correct-by-construction programs and libraries, in particular by automatic extraction of executable code (in OCaml, C, CakeML, etc.) from verified programs, and including innovative general methods like advanced ghost code, ghost monitoring, etc.
• Automated reasoning dedicated to deductive verification, so as to improve proof automation; improved combination of interactive provers and fully automated ones, proof by reflection.
• Improved feedback in case of proof failures: based on generation of counterexamples, or symbolic execution, or possibly randomized techniques à la quickcheck.
• Reduction of the trusted computing base in our toolchains: production of certificates from automatic proofs, for goal transformations (like those done by Why3), and from the generation of VCs

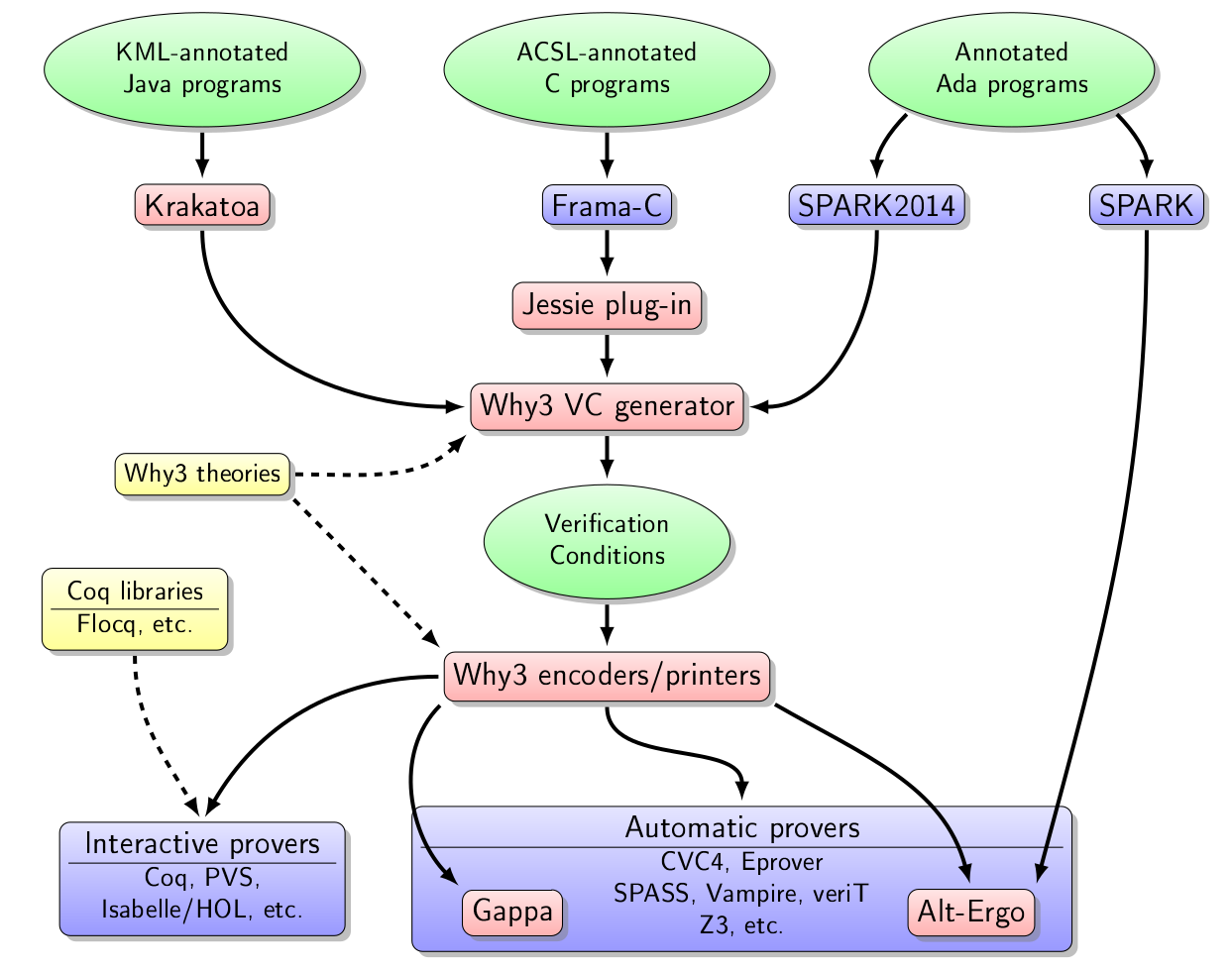
A significant part of the work achieved in this axis is related to the Why3 toolbox and its ecosystem, displayed on Figure 1. The boxes in red background correspond to the tools we develop in the Toccata team.

3.2 Reasoning on mutable memory in program verification

Permanent researchers: J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich

This axis concerns specifically the techniques for reasoning on programs where aliasing is the central issue. It covers the methods based on type-based alias analysis and related memory models, on specific program logics such as separation logics, and extended model-checking. It concerns the application on analysis of C or C++ codes, on Ada codes involving pointers, but also concurrent programs in general. The main topics planned are:

• The study of advanced type systems dedicated to verification, for controlling aliasing, and their use for obtaining easier-to-prove verification conditions. Modern typing system in the style of Rust, involving ownership and borrowing, will be considered.
• The design of front-ends of Why3 for the proofs of programs where aliasing cannot be fully controlled statically, via adequate memory models, aiming in particular at extraction to C; and also for concurrent programs.
• The continuation of fruitful work on concurrent parameterized systems, and its corresponding specific SMT-based model-checking.
• Concurrent programming on weak memory models, on one hand as an extension of parameterized systems above, but also in the specific context of OCaml multicore (http://ocamllabs.io/doc/multicore.html).
• In particular in the context of the ProofInUse joint lab, design methods for Ada, C, C++ or Java using memory models involving fine-grain analysis of pointers. Rust programs could be considered as well.

3.3 Verification of Computer Arithmetic

Permanent researchers: S. Boldo, C. Marché, G. Melquiond

We of course want to keep this axis which is a major originality of Toccata. The main topics of the next 4 years will be:

• Fundamental studies concerning formalization of floating-point computations, algorithms, and error analysis. Related to numerical integration, we will develop the relationships between mathematical stability and floating-point stability of numerical schemes.
• A significant effort dedicated to verification of numerical programs written in C, Ada, C++. This involves combining specifications in real numbers and computation in floating-point, and underlying automated reasoning techniques with floating-point numbers and real numbers. A new approach we have in mind concerns some variant of symbolic execution of both code and specifications involving real numbers.
• We have not yet studied embedded systems. Our approach is first to tackle numerical filters. This requires more results on fixed-point arithmetic and a careful study of overflows.
• Also a specific focus on arbitrary precision integer arithmetic, in the continuation of the ongoing PhD thesis of R. Rieu-Helft.

3.4 Spreading Formal Proofs

Permanent researchers: S. Boldo, S. Conchon, J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich

This axis covers applications in general. The applications we currently have in mind are:

• Hybrid Systems, i.e., systems mixing discrete and continuous transitions. This theme covers many aspects such as general techniques for formally reasoning of differential equations, and extending SMT-based reasoning. The challenge is to support both abstract mathematical reasoning and concrete program execution (e.g., using floating-point representation). Hybrid systems will be a common effort with other members of the future laboratory joint with LSV of ENS Cachan.
• Applied mathematics, in the continuation of the current efforts towards verification of Finite Element Method. It has only been studied in the mathematical point of view during this period. We plan to also consider their floating-point behavior and a demanding application is that of molecular simulation exhibited in the new EMC2 project. The challenge here is both in the mathematics to be formalized, in the numerical errors that have never been studied (and that may be huge in specific cases), and in the size of the programs, which requires that our tools scale.
• Continuation of our work on analysis of shell scripts. The challenge is to be able to analyze a large number of scripts (more than 30,000 in the corpus of Debian packages installation scripts) in an automatic manner. An approach that will be considered is some form of symbolic execution.
• Explore proof tools for mathematics, in particular automated reasoning for real analysis (application: formalization of the weak Goldbach conjecture), and in number theory.
• Obtain and distribute verified OCaml libraries, as expected outcome of the VOCaL project.
• Formalization of abstract interpretation and WP calculi: in the continuation of the former project Verasco, and an ongoing project proposal joint with CEA List. The difficulty of achieving full verification of such tools will be mitigated by use of certificate techniques.

4.1 Safety-Critical Software in Transportation

• Transfer to aeronautics: Airbus France Development of the control software of Airbus planes historically includes advanced usage of formal methods. A first aspect is the usage of the CompCert verified compiler for compiling C source code. Our work in cooperation with Gallium team for the safe compilation of floating-point arithmetic operations 2 is directly in application in this context. A second aspect is the usage of the Frama-C environment for static analysis to verify the C source code. In this context, both our tools Why3 and Alt-Ergo are indirectly used to verify C code.
• Transfer to the community of Atelier B In the former ANR project BWare, we investigated the use of Why3 and Alt-Ergo as an alternative back-end for checking proof obligations generated by Atelier B, whose main applications are railroad-related https://www.atelierb.eu/en/. The transfer effort continues nowadays through the FUI project LCHIP.
• ProofInUse joint lab: transfer to the community of Ada development

  Through the creation of the ProofInUse joint lab (https://www.adacore.com/proofinuse) in 2014, with AdaCore company (https://www.adacore.com/), we have a growing impact on the community of industrial development of safety-critical applications written in Ada. See the web page https://www.adacore.com/industries for a an overview of AdaCore's customer projects, in particular those involving the use of the SPARK Pro tool set. This impact involves both the use of Why3 for generating VCs on Ada source codes, and the use of Alt-Ergo for performing proofs of those VCs.

  The impact of ProofInUse can also be measured in term of job creation: the first two ProofInUse engineers, D. Hauzar and C. Fumex, employed initially on Inria temporary positions, have now been hired on permanent positions in AdaCore company. It is also interesting to notice that this effort allowed AdaCore company to get new customers, in particular the domains of application of deductive formal verification went beyond the historical domain of aerospace: application in automotive (https://www.adacore.com/customers/toyota-itc-japan) cyber-security (https://www.adacore.com/customers/multi-level-security-workstation), health (artificial heart, https://www.adacore.com/customers/total-artificial-heart).

4.2 Classification Algorithms of the Parcoursup Platform

ParcourSup (https://www.parcoursup.fr/) is the French national digital system for the orientation of new baccalaureate holders in institutions of higher education. This system uses specific algorithms to establish candidate rankings for each institution they are applying to. These rankings are produced according to the wishes of the candidates, the ranking of their applications by the establishments, taking into account general constraints on scholarship rates and rates of non-residents.

The expected properties of the algorithms in question are documented in natural language (https://framagit.org/parcoursup/algorithmes-de-parcoursup/blob/master/doc/presentation_algorithmes_parcoursup_2019.pdf). These algorithms are implemented in Java language, and their source code (https://framagit.org/parcoursup/algorithmes-de-parcoursup) is freely available under an open-source license.

In the year 2019 we have been involved in a project for verification of these algorithms. The choice of the proof environment to prove the ParcourSup algorithms could have naturally turner to our Krakatoa tool  57, 58, dedicated to Java, but this one is rather old: it only supports version 1.4 of Java (the Java code of ParcoursSup requires version 8), and is not really maintained due to lack of users. Other similar proof environments exist in the world, such as KeY  32 and VeriFast  51, but these tools do not support Java version 8 yet. The most promising candidate was OpenJML  47, which supports Java version 8.

In addition, our experience in proof of programs leads us to think that to prove the ParcourSup code, it is better to begin to consider an abstraction of the Java code, written directly in the intermediate language of Why3, in order to focus from the start on writing formal specifications necessary, then the search for the invariants to insert in the coded. The analysis with Why3 of 1-rate only algorithm allowed to validate several of the properties stated in the specification.

Later on, an analysis of Java code with OpenJML identified risks of errors in execution due to capacity overrun in calculations arithmetic. The proof of absence of run-time errors in this code was not fully achieved, we had to modify the Java code slightly. The original code was correct, but beyond the capabilities of OpenJML. The proof of the functional behavior of the Java code (properties described in the specification document in French) could not be made due to OpenJML limitations.

We finally implemented a new protoype JML2Why3 to go further in the proof of functional properties of the Java code. No only we were able to obtain again the proof of absence of overflow arithmetic and no null pointer dereferencing, but we could formally establish the property that the final call order is indeed a permutation (hence a bijection) of the initial list of wishes: in particular, no candidate can be forgotten by the code.

A report details the conclusion of this analysis 29.

4.3 Formal Analysis of Debian packages

Impactful results were produced in the context of the CoLiS project for the formal analysis of Debian packages. A first important step was the version 2 of the design of the CoLiS language done by B. Becker, C. Marché and other co-authors 38, that includes a modified formal syntax, a extended formal semantics, together with the design of concrete and symbolic interpreters. Those interpreters are specified and implemented in Why3, proved correct (following the initial approach for the concrete interpreter published in 2018 52 and an approach for symbolic interpretation 37), and finally extracted to OCaml code.

To make the extracted code effective, it must be linked together with a library that implements a solver for feature constraints 54, and also a library that formally specifies the behavior of basic UNIX utilities. The latter library is documented in details in a research report 53.

A third result is a large verification campaign running the CoLiS toolbox on all the packages of the current Debian distribution. The results of this campaign were reported in another article 15 that was presented at TACAS conference in 2020. The most visible side effect of this experiment is the discovery of bugs: more than 150 bug reports have been filled against various Debian packages.

4.4 Extensions of ProofInUse joint lab

The current plans for continuation of the ProofInUse joint lab (https://why3.gitlabpages.inria.fr/proofinuse/) include extension at a larger perimeter than Ada applications. We started to collaborate with the TrustInSoft company (https://trust-in-soft.com/) for the verification of C and C++ codes, including the use of Why3 to design verified and reusable C libraries (ongoing CIFRE PhD thesis). We also started to collaborate with Mitsubishi Electric in Rennes (http://www.mitsubishielectric-rce.eu/xindex.php) for a specific usage of Why3 for verifying embedded devices (logic controllers).

5.1 Awards

• Raphaël Rieu-Helft obtained the “Distinguished Student Author” award at the International Symposium on Symbolic and Algebraic Computation (ISSAC) Conference (https://www.sigsam.org/Awards/ISSACAwards.html) for his paper 21 written jointly with G. Melquiond. ISSAC is the top world conference on the domain of computer algebra.
• The Why3 software was awarded the “prix coup de cœur du Hub Open Source Systematic” https://systematic-paris-region.org/presse/why3-laureat-du-prix-coup-de-coeur-academique-du-hub-open-source-du-pole-systematic/

6.1 New software

7.1 Foundations and Spreading of Deductive Program Verification

• Certificates for Logic Transformations In a context of formal program verification, using automatic provers, the trusted code base of verification environments is typically very broad. An environment such as Why3 implements many complex procedures: generation of verification conditions, logical transformations of proof tasks, and interactions with external provers. Considering only the logical transformations of Why3, their implementation already amounts to more than 17,000 lines of OCaml code. In order to increase our confidence in the correction of such a verification tool, Garchery, Keller, Marché and Paskevich 23 proposed a mechanism of certifying transformations, producing certificates that can be validated by an external tool, according to the skeptical approach. They explored two methods to validate certificates: one based on a dedicated verifier developed in OCaml, the other based on the universal proof checker Dedukti. A specificity of their certificates is to be “small grains” and composable, which makes the approach incremental, allowing to gradually add new certifying transformations.
• Low Cost High Integrity Platform

  The purpose of the LCHIP project 25 is to ease the development of SIL4 certified systems and software, and to drastically reduce costs associated with their development. To achieve this goal, LCHIP combines a complete development environment for the B formal language and a safety executing platform.

  LCHIP avoids most testing by taking care of the verification of the software (type check, proof, compilation). The B method underlying this project enforces the development to be mathematically sound by producing proof obligations (PO). Those logical fomulas are expressed in first order logic extended with set theory and integer arithmetic. To target full proof automation of POs, the LCHIP platform integrates several automatic theorem provers. As a proof-of-concept, a connection to third-party provers has been conducted through the Why3 tool. This experiment produced excellent results in terms of proof automation, in particular for the Alt-Ergo prover.

• Simpler Proofs with Decentralized Invariants When verifying programs where the data have some recursive structure, it is natural to make use of global invariants that are themselves recursively defined. Though this is mathematically elegant, this makes the proofs more complex, as the preservation of these invariants now requires induction. In particular, this makes the proofs less amenable to automation. An alternative is to use local invariants attached to individual components of the structure and which only involve a bounded number of elements. These are called decentralized invariants. When the structure is updated, the footprint of the modification only impacts a bounded number of invariants and reestablishing them does not require induction. In this paper 13, Filliâtre illustrates this idea on three non-trivial programs, for which fully automated proofs are achieved.
• Abstraction and Genericity in Why3 The benefits of modularity in programming — abstraction barriers, which allow hiding implementation details behind an opaque interface, and genericity, which allows specializing a single implementation to a variety of underlying data types — apply just as well to deductive program verification, with the additional advantage of helping the automated proof search procedures by reducing the size and complexity of the premises and by instantiating and reusing once-proved properties in a variety of contexts. Filliâtre and Paskevich wrote a paper 19 demonstrating the modularity features of WhyML, the language of the program verification tool Why3. Instead of separating abstract interfaces and fully elaborated implementations, WhyML uses a single concept of module, a collection of abstract and concrete declarations, and a basic operation of cloning which instantiates a module with respect to a given partial substitution, while verifying its soundness. This mechanism brings into WhyML both abstraction and genericity, which is illustrated on a small verified Bloom filter implementation, translated into executable idiomatic C code.
• Continuation Passing as an Abstract Syntax for Deductive Verification A. Paskevich proposed a continuation passing style to devise an extremely economical abstract syntax for a generic algorithmic language 31. This syntax is flexible enough to naturally express conditionals,loops, (higher-order) function calls, and exception handling. It is type-agnostic and state-agnostic, which means that it can be combined with a wide range of type and effect systems. It is argued that this syntax is also well suited for the purposes of deductive verification. Indeed, that work shows how this syntax can be augmented in a natural way with specification annotations, ghost code, and side-effect discipline. Rules of verification condition generation are defined for this syntax, and it appears that the resulting formulas are nearly identical to what traditional approaches, like the weakest precondition calculus, produce for the equivalent algorithmic constructions. This constitutes a minimalistic yet versatile abstract syntax for annotated programs for which one can compute verification conditions without sacrificing their size, legibility, and amenability to automated proof, compared to more traditional methods. We believe that it makes it an excellent candidate for internal code representation in program verification tools.

7.2 Reasoning on mutable memory in program verification

• Ghost Monitors

  M. Clochard, C. Marché and A. Paskevich proposed a new approach to deductive program verification based on auxiliary programs called ghost monitors. This technique is useful when the syntactic structure of the target program is not well suited for verification, for example, when an essentially recursive algorithm is implemented in an iterative fashion. This new approach consists in implementing, specifying, and verifying an auxiliary program that monitors the execution of the target program, in such a way that the correctness of the monitor entails the correctness of the target. The ghost monitor maintains the necessary data and invariants to facilitate the proof. It can be implemented and verified in any suitable framework, which does not have to be related to the language of the target programs. This technique is also applicable when one wants to establish relational properties between two target programs written in different languages and having different syntactic structure.

  Ghost monitors can be used to specify and prove fine-grained properties about the infinite behaviors of target programs. Since this cannot be easily done using existing verification frameworks, this work introduces a dedicated language for ghost monitors, with an original construction to catch and handle divergent executions. The soundness of the underlying program logic is established using a particular flavor of transfinite games. This language and its soundness are formalized and mechanically checked. 17

• Deductive program verification for a language with a Rust-like typing discipline When verifying programs using a mutable heap, it is often required to show that pointers do not alias each other, ensuring there is only one way to modify structures in memory. This leads to cumbersome proof obligations and makes verification much more challenging. Newer languages like Rust feature pointers as well but prevent aliasing through the type system. This opens the door to simpler approaches to verification, free of tedious proof obligations. In his master thesis, X. Denis proposed a technique for the verification of Rust programs by translation to a functional language. The challenge of this translation is the handling of mutable borrows: pointers which control of aliasing in a region of memory. To overcome this, he used a technique inspired by prophecy variables to predict the final values of borrows. 30
• Verification of Programs with Pointers in SPARK G.-A. Jaloyan (CEA), C. Dross (AdaCore), M. Maalej (AdaCore), Y. Moy (AdaCore) et A. Paskevich introduced pointers to SPARK, a well-defined subset of the Ada language, intended for formal verification 20. In this work, the alias safety is ensured by a permission-based static alias analysis method inspired by Rust's borrow-checker and affine types. This extension has been implemented in the SPARK GNATprove formal verification toolset for Ada.
• Parameterized Model Checking on the TSO Weak Memory Model Modern multiprocessors and microprocessors implement weak or relaxed memory models, in which the apparent order of memory operation does not follow the sequential consistency (SC) proposed by Leslie Lamport. Any concurrent program running on such architecture and designed with an SC model in mind may exhibit new behaviors during its execution, some of which may potentially be incorrect. For instance, a mutual exclusion algorithm, correct under an interleaving semantics, may no longer guarantee mutual exclusion when implemented on a weaker architecture. Reasoning about the semantics of such programs is a difficult task. Moreover, most concurrent algorithms are designed for an arbitrary number of processes. D. Declerck, S. Conchon and F. Zaïdi proposed an approach to ensure the correctness of such concurrent algorithms, regardless of the number of processes involved. It relies on the Model Checking Modulo Theories framework, developed by Ghilardi and Ranise, which allows for the verification of safety properties of parameterized concurrent programs, that is to say, programs involving an arbitrary number of processes. This technology is extended with a theory for reasoning about weak memory models. The result is an extension of the Cubicle model checker called Cubicle-W, which allows the verification of safety properties of parameterized transition systems running under a weak memory model similar to TSO. 12

7.3 Verification of Computer Arithmetic

• WhyMP, a Formally Verified Arbitrary-Precision Integer Library The WhyMP library implements some algorithms of the GNU Multi-Precision library (GMP), the state-of-the-art C library for performing computations on arbitrary-precision integers. WhyMP is written in WhyML, the programming language offered by the Why3 software verification framework, and the functional correctness of the algorithms is formally verified. The WhyML code is then extracted as a C library that is binary-compatible with GMP and can be substituted to it in existing programs. Performance-wise, it is competitive with the no-assembly version of GMP, for small and medium-sized inputs 2127.
• Optimal Inverse Projection of Floating-Point Addition In a setting where we have intervals for the values of floating-point variables $x$, $a$, and $b$, we are interested in improving these intervals when the floating-point equality $x\oplus a=b$ holds. This problem is common in constraint propagation, and called the inverse projection of the addition. D. Gallois-Wong, S. Boldo, and P. Cuoq proposed floating-point theorems that provide optimal bounds for all the intervals 14.
• Emulating round-to-nearest-ties-to-zero "augmented" floating- point operations The 2019 version of the IEEE 754 Standard for Floating-Point Arithmetic recommends that new “augmented” operations should be provided for the binary formats. These operations use a new “rounding direction”: round to nearest ties-to-zero. S. Boldo, C. Lauter, and J.-M. Muller show how they can be implemented using the currently available operations, using round-to-nearest ties-to-even with a partial formal proof of correctness 11.
• A Correctly-Rounded Fixed-Point-Arithmetic Dot-Product Algorithm Dot products are ubiquitous in matrix computations, for instance in signal processing. We are especially interested in digital filters, where they are the core operation. We therefore focus on fixed-point arithmetic, used in embedded systems for time and energy efficiency. Common dot product algorithms ensure faithful rounding. For the sake of accuracy and reproducibility, we want to ensure correct rounding. We developed an algorithm that computes a correctly-rounded sum of products from inputs whose format is known in advance 16

7.4 Spreading Formal Proofs

• Formal Analysis of Debian packages

  Several new results were produced in the context of the CoLiS project for the formal analysis of Debian packages. A first important step is the version 2 of the design of the CoLiS language done by B. Becker, C. Marché and other co-authors 38, that includes a modified formal syntax, a extended formal semantics, together with the design of concrete and symbolic interpreters. Those interpreters are specified and implemented in Why3, proved correct (following the initial approach for the concrete interpreter published in 2018 52 and the recent approach for symbolic interpretation mentioned above 37), and finally extracted to OCaml code.

  To make the extracted code effective, it must be linked together with a library that implements a solver for feature constraints 54, and also a library that formally specifies the behavior of basic UNIX utilities. The latter library is documented in details in a research report 53.

  A third result is a large verification campaign running the CoLiS toolbox on all the packages of the current Debian distribution. The results of this campaign were reported in another article 15 that was presented at TACAS conference in 2020. The most visible side effect of this experiment is the discovery of bugs: more than 150 bugs report have been filled against various Debian packages.

• Functional Programming. At JFLA 2020, J.-C. Filliâtre gave a talk related to the elimination of non-tail calls 22. The example taken is that of a small recursive function to compute the height of a binary tree. Several solutions to avoid a stack overflow are given, compared, and discussed according to the programming language.
• A Coq retrospective — at the heart of Coq architecture, the genesis of version 7.0 During Fall 1999, J.-C. Filliâtre designed and implemented a new architecture for the Coq proof assistant, to isolate a “kernel of trust”. This architecture is still in use today. In June 2020, J.-C. Filliâtre was invited speaker at the Coq Workshop 24 to give an account on that work.
• Formal Verification of “ParcourSup” algorithms. A first part of this work was the verification of the first algorithm of Parcoursup using Why3. Most of the expected properties, taken from the public description of Parcoursup's algorithms, have been verified 33. We then worked on the verification of the Java source code of ParcourSup. The findings and lessons learnt are described in a report 29.
• An Early-Stage Prototype of a Key Server Developed using Why3 In the context of the VerifyThis Collaborative Long Term Challenge 2020 (https://verifythis.github.io/), we used the Why3 verification framework to design, from scratch, a simple but running prototype implementation of a PGP key server. We exploit the ability of Why3 to extract OCaml code from verified WhyML code so as to produce code that can be compiled into an executable. Our prototype is made of a combination of unverified handwritten OCaml code and of WhyML code whose functional behaviour is formally specified and proven correct 18.

8.1 ProofInUse-AdaCore Collaboration

Participants: Claude Marché, Jean-Christophe Filliâtre, Andrei Paskevich, Guillaume Melquiond, Benedikt Becker.

This collaboration is a joint effort of the Inria project-team Toccata and the AdaCore company which provides development tools for the Ada programming language. It is funded by a 5-year bilateral contract from Jan 2019 to Dec 2023.

The SME AdaCore is a software publisher specializing in providing software development tools for critical systems. A previous successful collaboration between Toccata and AdaCore enabled Why3 technology to be put into the heart of the AdaCore-developed SPARK technology.

The objective of ProofInUse-AdaCore is to significantly increase the capabilities and performances of the Spark/Ada verification environment proposed by AdaCore. It aims at integration of verification techniques at the state-of-the-art of academic research, via the generic environment Why3 for deductive program verification developed by Toccata.

8.2 ProofInUse-MERCE Collaboration

Participants: Claude Marché, Guillaume Melquiond, Cláudio Belo Lourenço.

This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company Mitsubishi Electric R&D (MERCE) in Rennes. It is funded by a bilateral contract of 18 months from Nov 2019 to April 2021.

MERCE has strong and recognized skills in the field of formal methods. In the industrial context of the Mitsubishi Electric Group, MERCE has acquired knowledge of the specific needs of the development processes and meets the needs of the group in different areas of application by providing automatic verification and demonstration tools adapted to the problems encountered.

The objective of ProofInUse-MERCE is to significantly improve on-going MERCE tools regarding the verification of Programmable Logic Controllers and also regarding the verification of numerical C codes.

8.3 ProofInUse-TrustInSoft Collaboration

Participants: Claude Marché, Guillaume Melquiond.

This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company TrustInSoft in Paris. It is funded by a bilateral contract of 18 months from Dec 2020 to April 2022.

TrustInSoft is an SME that offers the TIS-Analyzer environment for analysis of safety and security properties of source codes written in C and C++ languages. A version of TIS-Analyzer is available online, under the name TaaS (TrustInSoft as a Service, https://taas.trust-in-soft.com/).

The objective of ProofInUse-TrustInSoft is to integrate Deductive Verification in the platform TIS-Analyzer, with a special interest in the generation of counterexample to help the user in case of proof failure.

8.4 CEA-DAM Collaboration

Participants: Sylvie Boldo, Louise Ben Salem-Knapp.

A contract will be signed in 2021 between the CEA-DAM (“Direction des applications militaires”) and Toccata about the management of the PhD thesis of Louise Ben Salem-Knapp with William Weens (CEA-DAM) and Guillaume Perrin (CEA-DAM).

This topic of the PhD is between computer science and applied mathematics. We consider algorithms from numerical analysis and verify their good behavior on computers. This behavior, proven by supposing that the computations are perfect, could be put in fault by the problems of round-off errors and of overflows due to computations in floating-point arithmetic. We plan to study the impact of round-off errors in a hydrodynamic code. Hydrodynamics is the skeleton model of many physical models used in industry. It contains numerous technical, mathematical and numerical difficulties, which does not prevent its massive use in the simulation industry on increasingly complex problems. Today, the resolution of such problems requires the use of super-calculators, as well as the implementation of algorithms adapted to massively parallel calculation. The very large number of calculations required to produce results raises the question of their numerical quality.

8.5 CIFRE contract with TrustInSoft company

Participants: Guillaume Melquiond, Raphaël Rieu-Helft.

Jointly with the thesis of R. Rieu-Helft, supervised in collaboration with the TrustInSoft company, we established a 3-year bilateral collaboration contract, that ended in November 2020. The aim is to design methods that make it possible to design an arbitrary-precision integer library that, while competitive with the state-of-the-art library GMP, is formally verified. Not only are GMP's algorithm especially intricate from an arithmetic point of view, but numerous tricks were also used to optimize them. We are using the Why3 programming language to implement the algorithms, we are developing reflection-based procedures to verify them, and we finally extract them as a C library that is binary-compatible with GMP 921. The PhD thesis has been defended in Nov. 2020 27.

9.1 European Initiatives

9.2 National Initiatives

10.1 Promoting Scientific Activities

10.2 Teaching - Supervision - Juries

10.3 Popularization

11.1 Major publications

• 1 articleFrançoisF. Bobot, Jean-ChristopheJ.-C. Filliâtre, ClaudeC. Marché and AndreiA. Paskevich. Let's Verify This with Why3International Journal on Software Tools for Technology Transfer (STTT)1762015, 709--727
  HALback to text
• 2 articleSylvieS. Boldo, Jacques-HenriJ.-H. Jourdan, XavierX. Leroy and GuillaumeG. Melquiond. Verified Compilation of Floating-Point ComputationsJournal of Automated Reasoning542February 2015, 135-163URL: https://hal.inria.fr/hal-00862689
  back to textback to text
• 3 bookSylvieS. Boldo and GuillaumeG. Melquiond. Computer Arithmetic and Formal Proofs: Verifying Floating-point Algorithms with the Coq SystemISTE Press - ElsevierDecember 2017, URL: https://hal.inria.fr/hal-01632617
  back to text
• 4 articleMartinM. Clochard, LéonL. Gondelman and MárioM. Pereira. The Matrix ReprovedJournal of Automated Reasoning6032018, 365--383URL: https://hal.inria.fr/hal-01617437
  back to text
• 5 inproceedingsSylvainS. Conchon, MohamedM. Iguernlala, KailiangK. Ji, GuillaumeG. Melquiond and ClémentC. Fumex. A Three-tier Strategy for Reasoning about Floating-Point Numbers in SMTComputer Aided Verification2017, URL: https://hal.inria.fr/hal-01522770
  back to text
• 6 articleJean-ChristopheJ.-C. Filliâtre, LéonL. Gondelman and AndreiA. Paskevich. The Spirit of Ghost CodeFormal Methods in System Design4832016, 152--174URL: https://hal.archives-ouvertes.fr/hal-01396864v1
  back to text
• 7 inproceedingsClémentC. Fumex, ClaireC. Dross, JensJ. Gerlach and ClaudeC. Marché. Specification and Proof of High-Level Functional Properties of Bit-Level Programs8th NASA Formal Methods Symposium9690Lecture Notes in Computer ScienceMinneapolis, MN, USASpringerJune 2016, 291--306URL: https://hal.inria.fr/hal-01314876
  back to text
• 8 articleÉrikÉ. Martin-Dorel and GuillaumeG. Melquiond. Proving Tight Bounds on Univariate Expressions with Elementary Functions in CoqJournal of Automated Reasoning2016, URL: https://hal.inria.fr/hal-01086460
  back to text
• 9 inproceedingsGuillaumeG. Melquiond and RaphaëlR. Rieu-Helft. A Why3 Framework for Reflection Proofs and its Application to GMP's Algorithms9th International Joint Conference on Automated ReasoningLecture Notes in Computer ScienceOxford, United KingdomJuly 2018, URL: https://hal.inria.fr/hal-01699754
  back to textback to textback to text
• 10 inproceedingsPierreP. Roux, MohamedM. Iguernlala and SylvainS. Conchon. A Non-linear Arithmetic Procedure for Control-Command Software Verification24th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS)Thessalonique, GreeceApril 2018, URL: https://hal.archives-ouvertes.fr/hal-01737737
  back to text

11.2 Publications of the year

11.3 Cited publications

• 32 book W. Ahrendt B. Beckert R. Bubel R. Hähnle P. Schmitt M. Ulbrich Deductive Software Verification - The KeY Book - From Theory to Practice 10001 Lecture Notes in Computer Science Springer December 2016
  back to text
• 33 techreportLéoL. Andrès. Vérification par preuve formelle de propriétés fonctionnelles d'algorithme de classificationUniversité Paris SudAugust 2019, URL: https://hal.inria.fr/hal-02421484
  back to text
• 34 inproceedingsAliA. Ayad and ClaudeC. Marché. Multi-Prover Verification of Floating-Point ProgramsFifth International Joint Conference on Automated Reasoning6173Lecture Notes in Artificial IntelligenceEdinburgh, ScotlandSpringerJuly 2010, 127--141URL: http://hal.inria.fr/inria-00534333
  back to text
• 35 inproceedingsClarkC. Barrett, Christopher L.C. Conway, MorganM. Deters, LianaL. Hadarean, DejanD. Jovanović, TimT. King, AndrewA. Reynolds and CesareC. Tinelli. CVC4Proceedings of the 23rd international conference on Computer aided verificationCAV'11Berlin, HeidelbergSnowbird, UTSpringer-Verlag2011, 171--177
  back to text
• 36 manual PatrickP. Baudin, Jean-ChristopheJ.-C. Filliâtre, ClaudeC. Marché, BenjaminB. Monate, YannickY. Moy and VirgileV. Prevosto. ACSL: ANSI/ISO C Specification Language, version 1.4 2009
  back to text
• 37 inproceedingsBenediktB. Becker and ClaudeC. Marché. Ghost Code in Action: Automated Verification of a Symbolic InterpreterVerified Software: Tools, Techniques and Experiments12031Lecture Notes in Computer ScienceNew York, United StatesJuly 2019, URL: https://hal.inria.fr/hal-02276257
  back to textback to textback to text
• 38 techreportBenediktB. Becker, ClaudeC. Marché, NicolasN. Jeannerod and RalfR. Treinen. Revision 2 of CoLiS language: formal syntax, semantics, concrete and symbolic interpretersHAL Archives OuvertesOctober 2019, URL: https://hal.inria.fr/hal-02321743
  back to textback to text
• 39 inproceedingsPatrickP. Behm, PaulP. Benoit, AlainA. Faivre and Jean-MarcJ.-M. Meynadier. METEOR : A successful application of B in a large projectProceedings of FM'99: World Congress on Formal MethodsLecture Notes in Computer Science (Springer-Verlag)Springer VerlagSeptember 1999, 369--387
  back to text
• 40 inproceedingsSylvieS. Boldo, FrançoisF. Clément, Jean-ChristopheJ.-C. Filliâtre, MicaelaM. Mayero, GuillaumeG. Melquiond and PierreP. Weis. Formal Proof of a Wave Equation Resolution Scheme: the Method ErrorProceedings of the First Interactive Theorem Proving Conference6172LNCSEdinburgh, ScotlandSpringerJuly 2010, 147--162URL: http://hal.inria.fr/inria-00450789/
  back to text
• 41 articleSylvieS. Boldo, FrançoisF. Clément, Jean-ChristopheJ.-C. Filliâtre, MicaelaM. Mayero, GuillaumeG. Melquiond and PierreP. Weis. Wave Equation Numerical Resolution: a Comprehensive Mechanized Proof of a C ProgramJournal of Automated Reasoning504April 2013, 423--456URL: http://hal.inria.fr/hal-00649240/en/
  back to text
• 42 inproceedingsSylvieS. Boldo, Jean-ChristopheJ.-C. Filliâtre and GuillaumeG. Melquiond. Combining Coq and Gappa for Certifying Floating-Point Programs16th Symposium on the Integration of Symbolic Computation and Mechanised Reasoning5625Lecture Notes in Artificial IntelligenceGrand Bend, CanadaSpringerJuly 2009, 59--74
  back to text
• 43 articleSylvieS. Boldo and ClaudeC. Marché. Formal verification of numerical programs: from C annotated programs to mechanical proofsMathematics in Computer Science542011, 377--393URL: http://hal.inria.fr/hal-00777605
  back to textback to text
• 44 articleSylvieS. Boldo and Thi Minh TuyenT. Nguyen. Proofs of numerical programs when the compiler optimizesInnovations in Systems and Software Engineering722011, 151--160URL: http://hal.inria.fr/hal-00777639
  back to text
• 45 articleLilianL. Burdy, YoonsikY. Cheon, David R.D. Cok, Michael D.M. Ernst, Joeseph R.J. Kiniry, Gary T.G. Leavens, K. Rustan M.K. Leino and ErikE. Poll. An overview of JML tools and applicationsInternational Journal on Software Tools for Technology Transfer (STTT)73June 2005, 212--232
  back to text
• 46 inproceedingsArthurA. Charguéraud, Jean-ChristopheJ.-C. Filliâtre, CláudioC. Lourenço and MárioM. Pereira. GOSPEL --- Providing OCaml with a Formal Specification LanguageFM 2019 23rd International Symposium on Formal MethodsPorto, PortugalOctober 2019, URL: https://hal.inria.fr/hal-02157484
  back to text
• 47 inproceedingsDavid R.D. Cok. OpenJML: Software Verification for Java 7 using JML, OpenJDK, and EclipseProceedings 1st Workshop on Formal Integrated Development Environment149EPTCS2014, 79--92
  back to text
• 48 inproceedings SylvainS. Conchon, AlbinA. Coquereau, MohamedM. Iguernlala and AlainA. Mebsout. Alt-Ergo 2.2 SMT Workshop: International Workshop on Satisfiability Modulo Theories Oxford, United Kingdom July 2018
  HAL back to text
• 49 articleSylvainS. Dailler, DavidD. Hauzar, ClaudeC. Marché and YannickY. Moy. Instrumenting a Weakest Precondition Calculus for Counterexample GenerationJournal of Logical and Algebraic Methods in Programming992018, 97--113URL: https://hal.inria.fr/hal-01802488
  back to text
• 50 inproceedingsClémentC. Fumex, ClaudeC. Marché and YannickY. Moy. Automating the Verification of Floating-Point ProgramsVerified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/hal-01534533/
  back to text
• 51 inproceedingsBartB. Jacobs, JanJ. Smans, PieterP. Philippaerts, FrédéricF. Vogels, WillemW. Penninckx and FrankF. Piessens. VeriFast: A Powerful, Sound, Predictable, Fast Verifier for C and JavaNASA Formal Methods6617Lecture Notes in Computer ScienceSpringer2011, 41--55
  back to text
• 52 inproceedingsNicolasN. Jeannerod, ClaudeC. Marché and RalfR. Treinen. A Formally Verified Interpreter for a Shell-like Programming LanguageVerified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/
  back to textback to text
• 53 techreportNicolasN. Jeannerod, YannY. Régis-Gianas, ClaudeC. Marché, MihaelaM. Sighireanu and RalfR. Treinen. Specification of UNIX UtilitiesHAL Archives OuvertesOctober 2019, URL: https://hal.inria.fr/hal-02321691
  back to textback to text
• 54 inproceedingsNicolasN. Jeannerod and RalfR. Treinen. Deciding the First-Order Theory of an Algebra of Feature Trees with Updates9th International Joint Conference on Automated ReasoningOxford, United KingdomJuly 2018, URL: https://hal.archives-ouvertes.fr/hal-01807474
  back to textback to text
• 55 articleGerwinG. Klein, JuneJ. Andronick, KevinK. Elphinstone, GernotG. Heiser, DavidD. Cock, PhilipP. Derrin, DhammikaD. Elkaduwe, KaiK. Engelhardt, RafalR. Kolanski, MichaelM. Norrish, ThomasT. Sewell, HarveyH. Tuch and SimonS. Winwood. seL4: Formal verification of an OS kernelCommunications of the ACM536June 2010, 107--115
  back to text
• 56 articleXavierX. Leroy. A formally verified compiler back-endJournal of Automated Reasoning4342009, 363--446URL: http://hal.inria.fr/inria-00360768/en/
  back to text
• 57 articleClaudeC. Marché, ChristineC. Paulin-Mohring and XavierX. Urbain. The Tool for Certification of /JavaCard Programs annotated in 'Journal of Logic and Algebraic Programming581--22004, 89--106
  back to text
• 58 misc ClaudeC. Marché. The Krakatoa tool for Deductive Verification of Java Programs January 2009
  back to text
• 59 book Jean-MichelJ.-M. Muller, NicolasN. Brunie, FlorentF. de Dinechin, Claude-PierreC.-P. Jeannerod, MioaraM. Joldes, VincentV. Lefèvre, GuillaumeG. Melquiond, NathalieN. Revol and SergeS. Torres. Handbook of Floating-point Arithmetic (2nd edition) Birkhäuser Basel July 2018
  HAL back to text
• 60 inproceedingsThi Minh TuyenT. Nguyen and ClaudeC. Marché. Hardware-Dependent Proofs of Numerical ProgramsCertified Programs and ProofsLecture Notes in Computer ScienceSpringerDecember 2011, 314--329URL: http://hal.inria.fr/hal-00772508
  back to text
• 61 articleFlorentF. de Dinechin, ChristophC. Lauter and GuillaumeG. Melquiond. Certifying the floating-point implementation of an elementary function using GappaIEEE Transactions on Computers6022011, 242--253URL: http://hal.inria.fr/inria-00533968/en/
  back to text
• 62 inbookStijnS. de Gouw, JurriaanJ. Rot, Frank S.F. de Boer, RichardR. Bubel and ReinerR. Hähnle. OpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst CaseComputer Aided Verification: 27th International Conference, CAV 2015, San Francisco, CA, USA, July 18-24, 2015, Proceedings, Part ID. KroeningC. PăsăreanuChamSpringer International Publishing2015, 273--289
  back to text
• 63 inproceedingsLeonardoL. de Moura and NikolajN. Bj\orner. Z3, An Efficient SMT SolverTACAS4963Lecture Notes in Computer ScienceSpringer2008, 337--340
  back to text