Keywords
Computer Science and Digital Science
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.7. High performance computing
- A6.5.2. Fluid mechanics
Other Research Topics and Application Domains
- B4.2.2. Fusion
1 Team members, visitors, external collaborators
Research Scientists
- Emmanuel Franck [INRIA, Researcher]
- Victor Michel-Dansac [INRIA, Researcher]
Faculty Members
- Philippe Helluy [Team leader, UNIV STRASBOURG, Professor, HDR]
- Clementine Courtes [UNIV STRASBOURG, Associate Professor]
- Michaël Gutnic [UNIV STRASBOURG, Associate Professor]
- Laurent Navoret [UNIV STRASBOURG, Associate Professor]
- Yannick Privat [UNIV STRASBOURG, Professor, HDR]
- Vincent Vigon [UNIV STRASBOURG, Associate Professor, from Apr 2022]
Post-Doctoral Fellow
- Youssouf Nasseri [INRIA, from Oct 2022]
PhD Students
- Mickael Bestard [UNIV STRASBOURG]
- Leo Bois [INRIA]
- Clément Flint [UNIV STRASBOURG]
- Romane Helie [UNIV STRASBOURG, ATER, from Oct 2022]
- Romane Helie [UNIV STRASBOURG, until Sep 2022]
- Guillaume Mestdagh [UNIV STRASBOURG, until Sep 2022]
- Tom Sprunck [UNIV STRASBOURG]
- Guillaume Steimer [INRIA]
Technical Staff
- Matthieu Boileau [CNRS, Engineer]
Administrative Assistant
- Ouiza Herbi [INRIA]
2 Overall objectives
TONUS has started in January 2014. It is a team of the Inria Nancy-Grand Est center. It is located in the mathematics institute (IRMA) of the University of Strasbourg.
The International Thermonuclear Experimental Reactor (ITER) is a large-scale scientific experiment that aims to demonstrate that it is possible to produce energy from fusion, by confining a very hot hydrogen plasma inside a toroidal chamber, called tokamak. In addition to physics and technology research, the design of tokamaks also requires mathematical modeling and numerical simulations on supercomputers.
The objective of the TONUS project is to deal with such mathematical and computing issues. We are mainly interested in kinetic, gyrokinetic and fluid simulations of tokamak plasmas. In the TONUS project-team we are working on the development of new numerical methods devoted to such simulations. We investigate several classical plasma models, study new reduced models and new numerical schemes adapted to these models. We implement our methods in two software projects: Selalib and SCHNAPS adapted to recent computer architectures.
We have strong relations with the CEA-IRFM team and participate in the development of their gyrokinetic simulation software GYSELA. We are involved in two Inria Project Labs, respectively devoted to tokamak mathematical modeling and high performance computing. The numerical tools developed from plasma physics can also be applied in other contexts. For instance, we collaborate with a small company in Strasbourg specialized in numerical software for applied electromagnetism. We also study kinetic acoustic models with the CEREMA and multiphase flows with EDF.
Finally, our topics of interest are at the interface between mathematics, computer science, High Performance Computing, physics and practical applications.
3 Research program
3.1 Kinetic models for plasmas
The fundamental model for plasma physics is the coupled Vlasov-Maxwell kinetic model: the Vlasov equation describes the distribution function of particles (ions and electrons), while the Maxwell equations describe the electromagnetic field. In some applications, it may be necessary to take relativistic particles into account, which leads to consider the relativistic Vlasov equation, even if in general, tokamak plasmas are supposed to be non-relativistic. The distribution function of particles depends on seven variables (three for space, three for the velocity and one for time), which yields a huge amount of computation. To these equations we must add several types of source terms and boundary conditions for representing the walls of the tokamak, the applied electromagnetic field that confines the plasma, fuel injection, collision effects, etc.
Tokamak plasmas possess particular features, which require developing specialized theoretical and numerical tools.
Because the magnetic field is strong, the particle trajectories have a very fast rotation around the magnetic field lines. A full resolution would require a prohibitive amount of computation. It is necessary to develop reduced models for large magnetic fields in order to obtain tractable calculations. The resulting model is called a gyrokinetic model. It allows us to reduce the dimensions of the problem. Such models are implemented in GYSELA and Selalib.
On the plasma boundary, the collisions can no longer be neglected. Fluid models, such as MagnetoHydroDynamics (MHD), become relevant again. For the good operation of the tokamak, it is necessary to control MHD instabilities that arise at the plasma boundary. Computing these instabilities requires special implicit numerical discretizations with excellent long time behavior.
In addition to theoretical modeling tools, it is necessary to develop numerical schemes adapted to kinetic, gyrokinetic and fluid models. Three kinds of methods are studied in TONUS: Particle-In-Cell (PIC) methods, semi-Lagrangian and fully Eulerian approaches.
3.2 Gyrokinetic models: theory and approximation
In most phenomena where oscillations are present, we can establish a three-model hierarchy: (i) the model parameterized by the oscillation period, (ii) the limit model and (iii) the two-scale model, possibly with its corrector. In a context where one wishes to simulate such a phenomenon where the oscillation period is small and the oscillation amplitude is not small, it is important to have numerical methods based on an approximation of the two-scale model. If the oscillation period varies significantly over the domain of simulation, it is important to have numerical methods that approximate properly and effectively the model parameterized by the oscillation period and the two-scale model. Implementing two-scale numerical methods (for instance by Frénod et al. 25) is based on a numerical approximation of the Two-Scale model. These are called of order 0. A Two-Scale Numerical Method is called of order 1 if it incorporates information from the corrector and from the equation of which this corrector is a solution. If the oscillation period varies between very small values and values of order 1, it is necessary to have new types of numerical schemes (Two-Scale Asymptotic Preserving Schemes of order 1 or TSAPS) that preserve the asymptotics between the model parameterized by the oscillation period and the Two-Scale model with its corrector. A first work in this direction has been initiated by Crouseilles et al. 24.
3.3 Semi-Lagrangian schemes
The TONUS team, and more generally the scientific computing team at IRMA Strasbourg, has a long and recognized experience in numerical methods for Vlasov-type equations. We are specialized in both particle and phase space solvers for the Vlasov equation: Particle-in-Cell (PIC) methods and semi-Lagrangian methods. We also have a long-standing collaboration with CEA Cadarache for the development of the GYSELA software for gyrokinetic tokamak plasmas.
The Vlasov and the gyrokinetic models are partial differential equations that express the transport of the distribution function in the phase space. In the original Vlasov case, the phase space is the six-dimension position-velocity space. For the gyrokinetic model, the phase space is five-dimensional because we consider only the parallel velocity in the direction of the magnetic field and the gyrokinetic angular velocity instead of three velocity components.
A few years ago, Eric Sonnendrücker and his collaborators introduced a new family of methods for solving transport equations in the phase space. This family of methods are the semi-Lagrangian methods. The principle of these methods is to solve the equation on a grid of the phase space. The grid points are transported with the flow of the transport equation for a time step and interpolated back periodically onto the initial grid. The method is then a mix of particle Lagrangian methods and Eulerian methods. The characteristics can be solved forward or backward in time leading to the Forward Semi-Lagrangian (FSL) or Backward Semi-Lagrangian (BSL) schemes. Conservative schemes based on this idea can be developed and are called Conservative Semi-Lagrangian (CSL).
GYSELA is a 5D full gyrokinetic code based on a classical backward semi-Lagrangian scheme (BSL) 30 for the simulation of core turbulence that has been developed at CEA Cadarache in collaboration with our team 27.
More recently, we have started to apply the semi-Lagrangian methods to more general kinetic equations. Indeed, most of the conservation laws of physics can be represented by a kinetic model with a small set of velocities. Compressible fluids or MHD equations have such representations. Semi-Lagrangian methods then become a very appealing and efficient approach for solving these equations.
3.4 PIC methods
Historically PIC methods have been very popular for solving the Vlasov equations. They make it possible to solve the equations in phase space at a relatively low cost. The main disadvantage of this approach is that, due to its random aspect, it produces an important numerical noise that has to be controlled in some way, for instance by regularizations of the particles, or by divergence correction techniques in the Maxwell solver. We have a long-standing experience in PIC methods and we started implementing them in Selalib. An important aspect is to adapt the method to new multicore computers. See the work by Crestetto and Helluy 23.
3.5 Fluid and reduced kinetic models for plasmas
As already said, kinetic plasmas computer simulations are very intensive, because of the gyrokinetic turbulence. In some situations, it is possible to make assumptions on the shape of the distribution function that simplify the model. We obtain in this way a family of fluid models or reduced models.
Assuming that the distribution function has a Maxwellian shape, for instance, we obtain the MagnetoHydroDynamic (MHD) model. It is physically valid only in some parts of the tokamak (at the edges for instance). The fluid model is generally obtained from the hypothesis that the collisions between particles are strong.
However, the reduction is not necessarily a consequence of collisional effects. Indeed, even without collisions, the plasma may still relax to an equilibrium state over sufficiently long time scales (Landau damping effect).
In the fluid or reduced-kinetic regions, the approximation of the distribution function could require fewer data while still achieving a good representation, even in the collisionless regime.
Therefore, a fluid or a reduced model is a model where the explicit dependency on the velocity variable is removed. In a more mathematical way, we consider that in some regions of the plasma, it is possible to exhibit a (preferably small) set of parameters that allows us to describe the main properties of the plasma with a generalized "Maxwellian” . Then
In this case it is sufficient to solve for . Generally, the vector is the solution of a first order hyperbolic system.
Another way to reduce the model is to try to find an abstract kinetic representation with a set of kinetic velocities as small as possible. The kinetic approach has then only a mathematical meaning. It allows solving very efficiently many equations of physics.
3.6 Numerical schemes
As previously indicated, an efficient method for solving the reduced models is the Discontinuous Galerkin (DG) approach. It is possible to make it of arbitrary order. It requires limiters when it is applied to nonlinear PDEs occurring for instance in fluid mechanics. But the reduced models that we intend to write are essentially linear. The nonlinearity is concentrated in a few coupling source terms.
In addition, this method, when written in a special set of variables, called the entropy variables, has nice properties concerning the entropy dissipation of the model. It opens the door to constructing numerical schemes with good conservation properties and no entropy dissipation, as already used for other systems of PDEs 31, 22, 29, 28.
3.7 Matrix-free implicit schemes
In tokamaks, the reduced model generally involves a lot of different time scales. Most of them, associated to the fastest waves, are not relevant to the tokamak simulation. In order to filter them out, it is necessary to adopt implicit solvers in time. When the reduced model is based on a kinetic interpretation, it is possible to construct implicit schemes that do not impose solving costly linear systems. In addition the resulting solver is stable even at a very high CFL (Courant–Friedrichs–Lewy) number.
3.8 Electromagnetic solvers
Accurate resolution of the electromagnetic fields is essential for proper plasma simulations. Thus it is important to use efficient solvers for the Maxwell systems and its asymptotics: Poisson equation and magnetostatics.
The proper coupling of the electromagnetic solver with the Vlasov solver is also crucial for ensuring conservation properties and stability of the simulation.
Finally, plasma physics implies very different time scales. It is thus very important to develop implicit Maxwell solvers and Asymptotic Preserving (AP) schemes in order to obtain good behavior on long time scales.
3.9 Coupling
The coupling of the Maxwell equations to the Vlasov solver requires some precautions. The most important one is to control the charge conservation errors, which are related to the divergence conditions on the electric and magnetic fields. We will generally use divergence correction tools for hyperbolic systems presented for instance in 21 (and the references therein).
3.10 Implicit solvers
As already pointed out, in a tokamak, the plasma presents several different space and time scales. It is not possible in practice to solve the initial Vlasov-Maxwell model. It is first necessary to establish asymptotic models by letting some parameters (such as the Larmor frequency or the speed of light) tend to infinity. This is the case for the electromagnetic solver. To address this issue, time-implicit solvers have to be implemented, in order to provide good approximations of stationary states, or of the solution to the magnetic induction equation or to the Poisson equation.
4 Application domains
4.1 Controlled fusion and ITER
The search for alternative energy sources is a major issue for the future. Among others, controlled thermonuclear fusion in a hot hydrogen plasma is a promising possibility. The principle is to confine the plasma in a toroidal chamber, called a tokamak, and to attain the necessary temperatures to sustain nuclear fusion reactions.The International Thermonuclear Experimental Reactor (ITER) is a tokamak being constructed in Cadarache, France. This was the result of a joint decision by an international consortium including the European Union, Canada, USA, Japan, Russia, South Korea, India and China. ITER is a huge project. As of today, the budget is estimated at 20 billion euros. The first plasma shot is planned for 2025 and the first deuterium-tritium operation for 2027. Many technical and conceptual difficulties have to be overcome before the actual exploitation of fusion energy. Consequently, much research has been carried out around magnetically confined fusion. Among these studies, it is important to carry out computer simulations of the burning plasma. Thus, mathematicians and computer scientists are also needed in the design of ITER. The reliability and the precision of numerical simulations allow a better understanding of the physical phenomena and thus would lead to better designs. TONUS's main involvement is in such research. The required temperatures to attain fusion are very high, of the order of a hundred million degrees. Thus it is imperative to prevent the plasma from touching the tokamak inner walls. This confinement is obtained thanks to intense magnetic fields. The magnetic field is created by poloidal coils, which generate the toroidal component of the field. The toroidal plasma current also induces a poloidal component of the magnetic field that twists the magnetic field lines. The twisting is very important for the stability of the plasma. The idea goes back to research by Tamm and Sakharov, two Russian physicists, in the 50's. Other devices are essential for the proper operation of the tokamak: a divertor for collecting the escaping particles, microwave heating for reaching higher temperatures, a fuel injector for sustaining the fusion reactions, toroidal coils for controlling instabilities, etc.
4.2 Other applications
The software and numerical methods that we develop can also be applied to other fields of physics or engineering.
- For instance, we have a collaboration with the company AxesSim in Strasbourg for the development of efficient Discontinuous Galerkin (DG) solvers on hybrid computers (CPU/GPU). The applications are electro-magnetic simulations for the conception of antennas, electronic devices or aircraft electromagnetic compatibility.
- The acoustic conception of large rooms requires huge numerical simulations. It is not always possible to solve the full wave equation and many reduced acoustic models have been developed. A popular model consists in considering "acoustic" particles moving at the speed of sound. The resulting Partial Differential Equation (PDE) is very similar to the Vlasov equation. The same modeling is used in radiation theory. We have started to work on the reduction of the acoustic particles model and realized that our reduction approach perfectly applies to this situation. A PhD with CEREMA (Centre d’études et d’expertise sur les risques, l’environnement, la mobilité et l’aménagement) has started in October 2015 (PhD of Pierre Gerhard). The objective was to investigate the model reduction and to implement the resulting acoustic model in our DG solver.
- In September 2017, we started a collaboration with EDF Chatou (PhD of Lucie Quibel) on the modeling of multiphase fluids with complex equations of state. The goal is to simulate the high temperature liquid-vapor flow occurring in a nuclear plant. Among others, we will apply our recent kinetic method for designing efficient implicit schemes for this kind of flows.
5 New software and platforms
5.1 New software
5.1.1 KOUGLOFV
-
Name:
Kinetic schemes On Unstructured Grids for Large Optimized Finite Volume simulations
-
Keywords:
Discontinuous Galerkin, Parallel numerical solvers
-
Functional Description:
This code, written with the RUST language, solves Mawell's equations on a generic tetrahedral mesh, for applications in electromagnetism. The underlying numerical method is stable without a restrictive CFL condition on the time step, and the quasi-explicit resolution ensures a low computational cost. Thanks to these properties, the code is able to handle multi-scale aspects in the mesh. In addition, the code is enhanced with shared-memory parallelization.
-
Contact:
Victor Michel-Dansac
6 New results
6.1 Numerical methods for fluids and plasma dynamics
6.1.1 CFL-less and parallel Discontinuous Galerkin solver
Participants: Philippe Helluy, Pierre Gerhard, Victor Michel-Dansac, Bruno Weber [AxesSim, Illkirch-Graffenstaden].
The Discontinuous Galerkin method is a general method for solving conservation laws. In 8, we described a parallel and quasi-explicit Discontinuous Galerkin (DG) kinetic scheme for solving systems of balance laws. The solver is unconditionally stable (i.e., the CFL number can be arbitrary) and has the complexity of an explicit scheme. It can be applied to any hyperbolic system of balance laws. In this work, we assessed the performance of the scheme in the particular case of the three-dimensional wave equation and of Maxwell's equations. We measured the benefit of the unconditional stability by performing experiments with very large CFL numbers. In addition, we investigated how to parallelize this method.
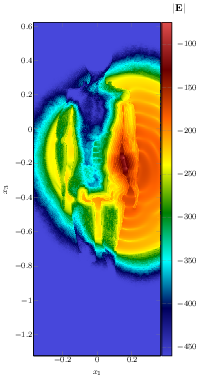
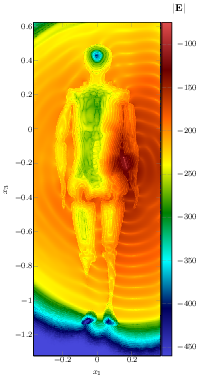
A version of this solver (presented in section 5.1.1), called KOUGLOFV, was implemented in the RUST language. It is a very reliable language that allows us to avoid most of the common memory bugs at compile time. It also provides nice tools for automatic and robust shared-memory parallelization. This parallelization was tested in the code, and good efficiency results were obtained. In 2022, KOUGLOFV was enhanced with distributed-memory parallelization (via MPI) and with the capability to handle large-scale simulations of electromagnetic waves within the human body, see figure 1. This led to the preprints 18 as well as the short report 19; the research was performed in the context of the grant detailed in section 7.1.
6.1.2 Generic high-order well-balanced numerical schemes
Participants: Christophe Berthon [Nantes University], Solène Bulteau [Maison de la Simulation, Saclay], Françoise Foucher [École Centrale de Nantes], Meissa M'Baye [Nantes University], Victor Michel-Dansac.
In 5, we considered a general framework to build a linear high-order well-balanced scheme for systems of balance laws. Such a framework is suited to almost any equation describing the motion of a fluid or a plasma. This article deals with a well-known issue of high-order well-balanced schemes. Indeed, such high-order schemes are based on a polynomial reconstruction, which must preserve the steady states under consideration in order to get the required well-balancedness property. A priori, to capture such a steady state, one needs to solve some strongly nonlinear equations. Here, a very easy, linear correction is designed under the generic framework of a system of hyperbolic balance laws, which describe most of the fluid or plasma systems. This correction can be applied to any scheme of order greater than or equal to 2, such as a MUSCL-type scheme, and ensures that this scheme exactly preserves the steady solutions. The main discrepancy with usual techniques lies in never having to invert the nonlinear function governing the steady solutions.
6.1.3 Third-order asymptotic-preserving scheme for the isentropic Euler equations
Participants: Victor Michel-Dansac, Andrea Thomann [JGU Mainz, Germany].
In 11, we developed of first order total variation diminishing (TVD) implicit-explicit (IMEX) Runge-Kutta (RK) schemes as a basis of a Multidimensional Optimal Order detection (MOOD) approach to approximate the solution of hyperbolic multi-scale equations. A key feature of our newly proposed TVD schemes is that the resulting CFL condition does not depend on the fast waves of the considered model, as long as they are integrated implicitly. However, a result from Gottlieb et al. 26 gives a first order barrier for unconditionally stable implicit TVD-RK schemes and TVD-IMEX-RK schemes with scale-independent CFL conditions. Therefore, the goal of this work is to consistently improve the resolution of a first-order IMEX-RK scheme, while retaining its stability and TVD properties. In this work we present a new approach based on a convex combination between a first-order TVD IMEX Euler scheme and a potentially oscillatory high-order IMEX-RK scheme. We derive and analyse the TVD property for a scalar multi-scale equation. In addition, we numerically assess the performance of our TVD schemes compared to standard -stable and SSP IMEX RK schemes from the literature. Finally, the resulting TVD-MOOD schemes are applied to the isentropic Euler equations, with very convincing results, see figure 2.
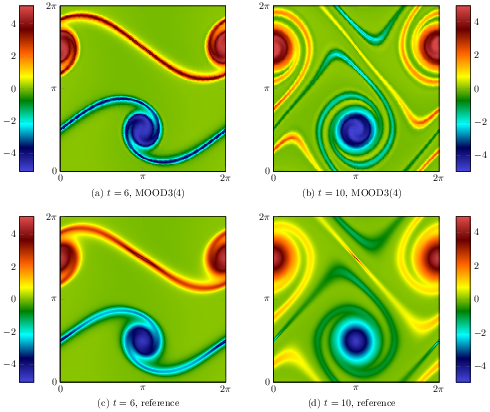
Double shear layer for the isentropic Euler equations
6.1.4 Optimal design of stellarators
Participants: Yannick Privat, Rémi Robin [Inria CAGE], Mario Sigalotti [Inria CAGE].
In 12, we have been interested, with M. Sigalotti and R. Robin, in the optimal design of stellarators, devices for the production of controlled nuclear fusion reactions, alternative to tokamaks. The confinement of the plasma is entirely achieved by a helical magnetic field created by the complex arrangement of coils powered by high currents around a toric domain. These coils describe a surface called “coil winding surface” (CWS). We modeled the design of the CWS as a shape optimization problem, so that the cost function reflects both the optimal plasma properties, through a least squares functional, and also manufacturability, through geometric terms involving the lateral surface and curvature of the CWS.
6.2 Other applications
While the main focus of the numerical tools we develop is plasma physics, they can also be used for other applications. We list below four such applications.
6.2.1 Reduced modeling and optimal control of epidemiological individual-based models with contact heterogeneity
Participants: Clémentine Courtès, Emmanuel Franck, Killian Lutz [École Centrale de Lyon & Institut Camille Jordan, Villeurbanne], Laurent Navoret, Yannick Privat.
Modeling epidemics using classical population-based models suffers from shortcomings that so-called individual-based models are able to overcome. They are able to take into account heterogeneity features, such as super-spreaders, and describe the dynamics involved in small clusters. In return, such models often involve large graphs which are expensive to simulate and difficult to optimize, both in theory and in practice. By combining the reinforcement learning philosophy with reduced models, we propose in 17 a numerical approach to determine optimal health policies for a stochastic individual-based model taking into account heterogeneity in the population. More precisely, we introduce a deterministic reduced population-based model involving a neural network, designed to faithfully mimic the local dynamics of the more complex individual-based model. Then the optimal control is determined by sequentially training the network until an optimal strategy for the population-based model succeeds in also containing the epidemic when simulated on the individual-based model. After describing the practical implementation of the method, several numerical tests are proposed to demonstrate its ability to determine controls for models with contact heterogeneity.
6.2.2 Optimal control for population dynamics
Participants: Luís Almeida [CNRS, LJLL, Inria MAMBA, Paris], Jesús Bellver Arnau [LJLL, Inria MAMBA, Paris], Michel Duprez [Inria MIMESIS, Strasbourg], Idriss Mazari [CEREMADE, Paris], Grégoire Nadin [CNRS, LJLL, Paris], Yannick Privat, Nicolas Vauchelet [Paris 13 University].
In collaboration with L. Almeida, J. Bellver Arnau, M. Duprez, G. Nadin, I. Mazari and N. Vauchelet, we pursued a series of works dedicated to the analysis and simulation of solutions of an optimal control problem motivated by population dynamics issues. In order to control the spread of mosquito-borne arboviruses, the sterile insect technique (SIT) consists in releasing mosquitoes infected with a bacterium called Wolbachia into the environment, which considerably reduces the transmission of the virus to humans. The goal is to effectively release the mosquitoes spatially so that the population of infected ones overwhelms the population of uninfected mosquitoes. Assuming very high fecundity rates, an asymptotic model on the proportion of infected mosquitoes is introduced, leading to an optimal control problem to determine the best spatial strategy to adopt.
We tackled the optimal strategy problem for SIT in 3 and 4, more specifically studying the robustness of optimal strategy for a general family of criteria and introduced an adapted optimization algorithm for computing optimal control strategies.
In addition, 10 is dedicated to the study of some qualitative properties of optimal control problems involving weighted eigenvalues and diffusion reaction systems used to describe the spatio-temporal dynamics of mosquito vectors of diseases such as dengue. This work, although fundamental and not dedicated to any particular application, have notably led to efficient optimization algorithms and analysis for the mentioned applied problems.
6.2.3 Gridless 3D Recovery of Image Sources from Room Impulse Responses
Participants: Tom Sprunck, Antoine Deleforge [Inria MULTISPEECH, Nancy], Yannick Privat, Cédric Foy [Cerema, Strasbourg].
In 13, we were interested in the reconstruction of the shape of a parallelepipedic room from measurements made by microphones during a certain time. A difficulty of this work was the fact that only the low frequency part of the signal is measured. We introduced a model and an efficient reconstruction algorithm for such shapes. We now seek to generalize our approach to any shape of room.
6.2.4 Other applications in (shape) optimization and optimal control
Participants: Benoît Braïda [Sorbonne Université, Paris], Jérémy Dalphin [EDF R&D, Saclay], Charles Dapogny [LJK, Grenoble], Pascal Frey [LJLL, Paris], Emmanuel Humbert [LMPT, Tours], Yannick Privat, Emmanuel Trélat [LJLL, Paris].
In 6, algorithms specific to a particular application, epidemiology or quantum chemistry, were obtained using a precise analysis of the model and the optimality conditions.
Finally, 9 contains fine analysis results of the "geometric quantity" for the wave equation with an internal control, corresponding to the minimum time taken on average by a geodesic to intersect the control set.
7 Bilateral contracts and grants with industry
7.1 Bilateral contracts with industry
Participants: Philippe Helluy, Victor Michel-Dansac, Pierre Gerhard.
We are involved in a common project with the company AxesSim in Strasbourg. The objective is to help to the development of a commercial software for the numerical simulation of electromagnetic phenomena. The applications are directed towards antenna design and electromagnetic compatibility. This project was partly supported by DGA through "RAPID" funds. A software engineer position (P. Gerhard) has started in 2021 on this subject. The objective is to implement a matrix-free CFL-less Discontinuous Galerkin (DG) scheme for solving Maxwell equations. In this way it is possible to get rid of the very small time steps imposed by small cells in automatically generated meshes. Preliminary results were very promising: stability and second order accuracy are observed for simulations with CFL numbers greater than 10. This project is supported by the Labex IRMIA++ (engineer position of P. Gerhard) and the French 2021 "Plan de relance": it allowed to host an AxesSim engineer in the Tonus team for one year for working on the joint DG solver.8 Partnerships and cooperations
8.1 International research visitors
8.1.1 Visits of international scientists
Other international visits to the team
Stéphane Clain
Participants: Philippe Helluy, Victor Michel-Dansac.
-
Status:
Full professor
-
Institution of origin:
Universidade do Minho
-
Country:
Portugal
-
Dates:
31/01/2023 – 04/02/2023
-
Context of the visit:
Discussing the treatment of boundary conditions with ROD methods
-
Mobility program/type of mobility:
Research stay
8.2 National initiatives
8.2.1 National projects
-
Étude de stratégies multi-échelles pour la simulation en compatibilité électromagnétique:
- Acronym: ANR M2CEM
- Duration: 01/2021 – 12/2023
- Coordinator: X. Ferrières, ONERA Toulouse
- Partners: Tonus, IRMA, AxesSim, ONERA
- Participants: Ph. Helluy, V. Michel-Dansac, P. Gerhard
- Abstract: The objective of this project is to improve the numerical solvers of the partners for electromagnetic compatibility simulations. These tools are applied for the design of antennae or connected objects. Several aspects will be explored: code coupling, adaptative time stepping, CFL-less schemes, locally implicit schemes, innovative time integrators and mesh management.
-
MOdeling and SImulation of COmplex Ferromagnetic systems:
- Acronym: ANR MOSICOF
- Duration: 10/2021 – 10/2025
- Coordinator: S. Labbé, Sorbonne Université
- Partners: Sorbonne université, Université de Pau et des Pays de l'Adour, Université de Strasbourg
- Participants: C. Courtès, Y. Privat
- Abstract: During the last decade, promising applications of ferromagnetic materials have emerged in the domains of nanoelectronics (spintronic) and data storage: complex ferromagnetic systems are increasingly used for digital data recording and logic devices. They reduce the energy storage cost while improving the performance of the devices. The goal of this proposal is to bring together mathematicians and physicists around the understanding of the properties of ferromagnetism. One of the main objectives is to highlight and treat new multi-physics models, allowing for optimization and control of the magnetizations, and to simulate the phenomena in a more efficient and less expensive way. We wish to develop approaches leading to mathematically justified and physically relevant solutions for the analysis and optimization of these materials, and which could ultimately lead to implementation on devices.
-
Machine Learning for Kinetic equations
- Acronym: ANR MILK
- Duration: 01/2022 – 12/2024
- Coordinator: E. Franck, Inria Nancy - Grand Est & E. Sonnendrücker, Technische Universität München (TUM)
- Partners: Inria Nancy - Grand Est & TUM
- Participants: C. Courtès, E. Franck, L. Navoret
- Abstract: Kinetic models are accurate descriptions of interacting particle systems in physics. However, their numerical resolution is often too demanding, as they are defined in the large-dimensional position/velocity phase space and involve multi-scale dynamics. For this reason, reduced models have been developed that represent optimal trade-offs between numerical cost and modeling completeness. In general, this reduction is carried out in two ways. The first is based on asymptotic models that filter out fast dynamics and are obtained when a small parameter tends towards zero (collision/oscillation limit). The second, called reduced order modeling, consists in finding a smaller representation of the problem able to describe the dynamics (POD). The main objective of this project is to design new reduced order models that are more efficient than classical ones, based on machine learning techniques applied to kinetic data. Ensuring the stability of the obtained models will be a key point of these studies.
9 Dissemination
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
- 08/2022: Summer school “Deep learning and applications”, Strasbourg, France(Clémentine Courtès , Laurent Navoret )
- 06/2022: Workshop IRMA/EDF on the modeling of multiphase flows, Strasbourg, (Philippe Helluy ).
- 06/2022: Minisymposium at ECCOMAS 2022 “Study of ferromagnetic systems”, Oslo, Norway (Clémentine Courtès )
- 06/2022: Minisymposium at ECCOMAS 2022 “Deep learning for Hamiltonian problems and variational analysis”, Oslo, Norway (Emmanuel Franck , Laurent Navoret , Yannick Privat )
- 06/2022: Minisymposium at ECCOMAS 2022 “Well-balanced schemes for hyperbolic systems with source terms”, Oslo, Norway (Victor Michel-Dansac )
- 01/2022: Master class: PDEs and machine learning, Strasbourg (Emmanuel Franck , Yannick Privat )
Member of the organizing committees
- Organizing committee of FVCA10, 30/10/2023 – 03/11/2023 (Clémentine Courtès , Emmanuel Franck , Philippe Helluy , Victor Michel-Dansac , Laurent Navoret )
- Organizing committee of CEMRACS2023, 17/07/2023 – 23/08/2023 (Victor Michel-Dansac )
- Organizing committee of CEMRACS2022, 18/07/2022 – 26/08/2022 (Emmanuel Franck , Laurent Navoret )
Seminar organization
- 09/2021 – now: Organization of the PDE Seminar at Strasbourg University (Clémentine Courtès and Victor Michel-Dansac )
- 01/2021 – now: Organization of the Machine Learning working group at Strasbourg University (Emmanuel Franck )
9.1.2 Journal
Member of the editorial boards
- Computational and Applied Mathematics (Yannick Privat )
- Numerical Algebra, Control & Optimization (Yannick Privat )
- Advances in Continuous and Discrete Models (Yannick Privat )
- Journal of Optimization, Theory and Applications (Yannick Privat )
- AIMS Applied Mathematics books (Yannick Privat )
- Evolution Equations and Control Theory (Yannick Privat )
Reviewer - reviewing activities
- Applied Mathematics and Computation (Victor Michel-Dansac )
- ESAIM: Mathematical Modeling and Numerical Analysis (Victor Michel-Dansac )
- Journal of Computational Physics (Victor Michel-Dansac , Laurent Navoret , Philippe Helluy )
- MathSciNet (Victor Michel-Dansac )
- Proceedings of the Combustion Institute (Matthieu Boileau )
- SIAM Journal on Scientific Computing (Victor Michel-Dansac )
- zbMath (Victor Michel-Dansac )
- CAMWA (Philippe Helluy )
- SMAI Journal of Computational Mathematics (Philippe Helluy )
9.1.3 Talks
- 12/2022: X/Stra Meeting, Strasbourg, France (Matthieu Boileau )
- 12/2022: Seminar of Numerical analysis of Coimbra university, (online) (Emmanuel Franck ).
- 12/2022: Seminar of Numerical analysis of CEA DAM (Emmanuel Franck ).
- 11/2022: GdR MOA 2022 workshop, Nice, France (Yannick Privat )
- 10/2022: Journée de restitution croisée Grands Challenges Genci, Gif-sur-Yvette, France (Matthieu Boileau )
- 09/2022: “New trends in complex fluids” workshop, Paris, France (Laurent Navoret )
- 09/2022: International Conference Zaragoza-Pau on Applied Mathematics and Statistics (Yannick Privat )
- 09/2022: DU ITI, univ. Strasbourg, France (Yannick Privat )
- 06/2022: Séminaire CEA SISMA, Bruyères le Chatel (Philippe Helluy )
- 06/2022: ANR MOSICOF workshop, Paris, France (Clémentine Courtès )
- 06/2022: HYP2022, Málaga, Spain (Victor Michel-Dansac )
- 06/2022: CANUM 2022, Évian, France (Yannick Privat )
- 05/2022: Seminar of the Reims math department, Reims, France (Clémentine Courtès )
- 05/2022: Applied mathematics seminar, Nantes, France (Victor Michel-Dansac )
- 04/2022: Structure-Preserving Discretizations for Nonlinear Systems of Hyperbolic, Involution-Constrained Partial Differential Equations on Manifolds, Oberwolfach, Germany (Philippe Helluy )
- 04/2022: M2N seminar – Mathematical and numerical modeling, CNAM, Paris, France (Victor Michel-Dansac )
- 03/2022: PDE days, Nancy, France (Clémentine Courtès )
- 03/2022: Analysis seminar, Strasbourg, France (Clémentine Courtès )
- 03/2022: Modeling and scientific computing seminar, Lyon, France (Clémentine Courtès )
- 03/2022: Applied Analysis seminar A3, Amiens, France (Victor Michel-Dansac )
- 03/2022: Workshop Mohycon, Pornichet, France (Emmanuel Franck )
- 02/2022: Tuto Techno Rust, Inria Nancy (Philippe Helluy )
- 02/2022. Workshop “Mathematical epidemiology”, Thematic trimester program at Institut Henri Poincaré, Paris, France (Yannick Privat )
- through 2022: many talks in the Machine Learning workgroup (Matthieu Boileau , Clémentine Courtès , Emmanuel Franck , Laurent Navoret , Victor Michel-Dansac , Yannick Privat , Vincent Vigon )
9.1.4 Research administration
- Manager of the “GDR Calcul” (Matthieu Boileau )
- Member of the direction of “GDR Calcul” (Emmanuel Franck )
- Member of the CdT Inria Nancy (Matthieu Boileau )
- until 09/2022: Head of the mathematics department in Strasbourg university (Michaël Gutnic )
- since 09/2022: Dean of the Mathematics and Computer Science faculty (Directeur de l'UFR Mathématique et Informatique) in Strasbourg university (Michaël Gutnic )
- Comex Inria Nancy-Grand-Est (Philippe Helluy )
- Elected member of the “Commission de la Recherche” of the University of Strasbourg (Philippe Helluy )
- Head of the CNRS Lab IRMA “Institut de Recherche Mathématique Avancée”, UMR 7501 (Philippe Helluy )
- 04/2021 – now: nominated member of the Inria Nancy - Grand Est “comité de centre” (Clémentine Courtès )
- 11/2019 – now: Member of CNU Section 26 (Yannick Privat )
- 04/2019 – now: Member of the IRMA expert committee (Yannick Privat )
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
- Licence 1, “Mathematics for biology”, 12h lectures + 23h exercise sessions, Strasbourg University, France (Michaël Gutnic )
- Licence 1, “Mathematics for health studies”, 36h, Strasbourg University, France (Michaël Gutnic )
- Licence 2, “Applied numerical analysis”, 18h, Strasbourg University, France (Clémentine Courtès )
- Licence 2, “Object-Oriented Programming in Python”, 16h lectures (Emmanuel Franck , Victor Michel-Dansac ) + 16h computer labs (Victor Michel-Dansac ), Strasbourg University, France
- Licence 2, “Scientific computing”, 20h lectures + 17h computer labs, Strasbourg University, France (Michaël Gutnic )
- “Probability and Statistics”, 30h, CNAM, France (Michaël Gutnic )
- Licence 3, “Numerical analysis techniques 1”, 32h lectures + problem sessions + computer labs, Strasbourg University, France (Clémentine Courtès )
- Licence 3, “Scientific computing”, 65h lectures + exercise sessions, Strasbourg University, France (Clémentine Courtès )
- Licence 3, “Nonlinear Optimization”, 61h lectures + exercise sessions, Strasbourg University, France (Clémentine Courtès )
- Licence 3, “Advanced C++”, 20h lectures (Emmanuel Franck ) + 34h computer labs (Emmanuel Franck ), Strasbourg University, France
- Licence 3, “Numerical analysis techniques 2”, 34h, Strasbourg University, France (Philippe Helluy )
- Licence 3, “Introduction to C++”, 34h, Strasbourg University, France (Philippe Helluy )
- Master 1, “Parallel Computing”, 20h, Strasbourg University, France (Matthieu Boileau )
- Master 1, “Machine Learning”, 4h lectures + 4h computer labs, Strasbourg University, France (Emmanuel Franck )
- Master 1 Pure Mathematics, “Scientific computing”, 13h lectures (Philippe Helluy ) + 14h computer labs (Philippe Helluy & Victor Michel-Dansac ), Strasbourg University, France
- Master 1 Applied Mathematics, “Scientific computing”, 35h, Strasbourg University, France (Laurent Navoret )
- Master 1, “Optimization”, 6h computer labs, Strasbourg University, France (Clémentine Courtès )
- Master 1, “Optimization”, 62.5h, Strasbourg University, France (Laurent Navoret )
- Master 1 Applied Mathematics, “Random models”, 35h, Strasbourg University, France (Vincent Vigon )
- Master 1 Applied Mathematics, “Data mining”, 35h, Strasbourg University, France (Vincent Vigon )
- Master 1 Applied Mathematics, “Signal processing”, 35h, Strasbourg University, France (Vincent Vigon )
- Master 1 DUAS, “Data science”, 50h, Strasbourg University, France (Vincent Vigon )
- Master 2 Cell Physics, “Basics in mathematics”, 24h, Strasbourg University, France (Laurent Navoret )
- Master 2 Cell Physics, “Math for living matter”, 6h, Strasbourg University, France (Laurent Navoret )
- Master 2 Agrégation, “Scientific computing”, 28h, Strasbourg University, France (Philippe Helluy )
- Master 2 Agrégation, “Analysis”, 7.5h, Strasbourg University, France (Laurent Navoret )
- Master 2 Agrégation, “Scientific computing”, 66h, Strasbourg University, France (Laurent Navoret )
- Master 2 Agrégation, “Text study”, 6h, Strasbourg University, France (Clémentine Courtès )
- Master 2 Agrégation, “Probability”, 50h, Strasbourg University, France (Vincent Vigon )
- Master 2 Pure Mathematics, “Nonlinear evolution PDEs”, 30h, Strasbourg University, France (Clémentine Courtès )
- Master 2, “Data Science”, 20h, Strasbourg University, France (Matthieu Boileau )
- Master 2, “Numerical methods for hyperbolic PDEs”, 35h, Strasbourg University, France (Philippe Helluy )
- Master 2, “Theory and numerics for incompressible fluids”, 10h, Sorbonne University, France (Yannick Privat )
- Master 2, “Variational Analysis and Planification”, 30h, Strasbourg University, France (Yannick Privat )
- Master 2, “Optimal control”, 70h, Strasbourg University, France (Yannick Privat )
- Master 2 Applied Mathematics, “Signal processing and deep learning”, 35h, Strasbourg University, France (Vincent Vigon )
- Master 2 Applied Mathematics, “Graphs and applications”, 35h, Strasbourg University, France (Vincent Vigon )
- Diplôme d'université, “Interdisciplinary seminars”, 22.5h, Strasbourg University, France (Laurent Navoret )
- Training Course, “Basics for scientific python”, 28h, Urfist (Unité Régionale de Formation à l'Information Scientifique et Technique), France (Matthieu Boileau )
9.2.2 Supervision
- M1 thesis: M. Marquat, “Introduction to the analysis of hyperbolic systems”, 02/2022 – 06/2022. Victor Michel-Dansac.
- M1 thesis: C. Schnoebelen, “Reduced models with geometric approaches”, 06/2022 – 08/2022. Emmanuel Franck and Laurent Navoret.
- M2 project: C. Holler, “Structure-preserving methods for PDEs”, 10/2021 – 01/2022. J. Aghili (IRMA Strasbourg), Emmanuel Franck and Victor Michel-Dansac.
- M2 thesis: R. Sublet, “Problèmes de classification et méthode des machines à vecteurs de support”, 12/2021 – 04/2022. Clémentine Courtès.
- M2 internship: V. Italiano, “Reduced Order Modeling For Highly Nonlinear PDEs Using Physics-Informed Neural Networks”, 02/2022 – 08/2022. H. Baty (Strasbourg Observatory), Emmanuel Franck, Victor Michel-Dansac and Vincent Vigon.
- PhD completed: J. B. Arnau, “Stratégie de contrôle d'une population de moustiques pour la lutte contre les arbovirus.” September 2019 – December 2022. Yannick Privat and L. Almeida (LJLL, Paris).
- PhD completed: G. Mestdagh, “Suivi de tumeur en temps réel par des méthodes d'optimisation”, Strasbourg university. September 2019 – December 2022. Yannick Privat and S. Cotin (Inria MIMESIS, Strasbourg).
- PhD in progress: R. Hélie, “Relaxation methods for kinetic models in plasma physics.”. Beginning: October 2019. Matthieu Boileau, Emmanuel Franck, Philippe Helluy and Laurent Navoret.
- PhD in progress: M. Bestard, “Optimal control for numerical simulation in physics plasma.”. Beginning: September 2020. Emmanuel Franck, Laurent Navoret and Yannick Privat.
- PhD in progress: L. Bois, “Machine learning for numerical methods. Application in plasma physics.”. Beginning: September 2020. Philippe Helluy, Emmanuel Franck, Laurent Navoret and Vincent Vigon.
- PhD in progress: C. Flint, “Efficient data compression for high-performance PDE solvers.”. Beginning: October 2020. Philippe Helluy and S. Genaud (ICube, Strasbourg).
- PhD in progress: T. Sprunck, “Can one hear the shape of a room?”. Beginning: September 2021. A. Deleforge (Inria MULTISPEECH, Nancy) and Yannick Privat.
- PhD in progress: N. Victorion, “Numerical methods assisted by deep learning for wave problems”. Beginning: September 2021. H. Barucq (Inria MAKUTU, Pau) and Emmanuel Franck.
- PhD in progress: G. Steimer, “Model reduction using deep learning for plasma physics”. Beginning: October 2021. R. Côte (IRMA Strasbourg), Emmanuel Franck and Laurent Navoret.
- PhD in progress: G. Lazare, “Simulations performantes en thermo-hydraulique des cœurs avec THYC”. Beginning: November 2022. Philippe Helluy and EDF Chatou.
- PhD in progress: M. Pallanque, “Radiative transfer models for astrophysical code”. Beginning: September 2022. P. Ocvirk (Strasbourg Observatory) and Emmanuel Franck
- Postdoc: G. Ferrière, “Stabilité et contrôle optimal de modèles ferromagnétiques”. Beginning: September 2021. R. Côte (IRMA Strasbourg), Clémentine Courtès and Yannick Privat.
- Postdoc: L. Godard-Cadillac, “Stabilité et contrôle d'un réseau de particules ferromagnétiques”. Beginning: September 2022. R. Côte (IRMA Strasbourg), Clémentine Courtès and Yannick Privat.
- Postdoc: Y. Nasseri, “Deep Moment models for colisional Vlasov equations ”. Beginning: October 2022. Vincent Vigon, Clémentine Courtès, Laurent Navoret and Emmanuel Franck .
9.2.3 Juries
- 12/2022: Reviewer for Irene Gómez-Bueno's PhD thesis, University of Málaga, Spain (Victor Michel-Dansac )
- 12/2022: Reviewer for S.-E. Zerrouq's PhD thesis, univ. Pau et des Pays de l’Adour, France (Yannick Privat )
- 12/2022: Reviewer for C. Qiu's PhD thesis, univ. Paris Saclay, France (Philippe Helluy )
- 12/2022: Member of the PhD committee for E. Bounre, univ. Aix-Marseille, France (Philippe Helluy )
- 12/2022: Reviewer for V. Vasanthan's PhD thesis, univ. Pau (Philippe Helluy )
- 11/2022: Reviewer for C. Mentuda's PhD thesis, univ. de Picardie Jules Verne, France (Yannick Privat )
- 09/2022: Reviewer for A. Bottois's PhD thesis, univ. Clermont-Auvergne, France (Yannick Privat )
- 09/2022: Reviewer for R. Robin's PhD thesis, Sorbonne univ., France (Yannick Privat )
- 07/2022: Member of the PhD committee for M. Nahon, univ. Savoie Mont-Blanc, France (Yannick Privat )
- 05-06/2022: Member of the “agrégation externe” jury (Clémentine Courtès , Emmanuel Franck )
- 05/2022: Grading papers for the “concours ENS section B/L” (Clémentine Courtès )
- 04/2022: Member of the PhD committee for Q. Holka, École des Mines de Paris, France (Yannick Privat )
- 03/2022: Member of the PhD committee for Meissa M'Baye, Nantes University, France (Victor Michel-Dansac )
- 02/2022: Reviewer for D. Ruiz Balet's PhD thesis, Madrid univ., France (Yannick Privat )
- 02/2022: Reviewer for K. Kozhanova's PhD thesis, Poitiers, France (Philippe Helluy )
9.2.4 Teaching administration
- Member of the “commission Parcoursup” (Clémentine Courtès )
- since 2021: Member of the “conseil de perfectionnement de la licence pluri-sciences” (Clémentine Courtès )
- 07/2021 – now: Head of the “Licence concours administratifs” (Clémentine Courtès )
- Director of studies of the Interdisciplinary Thematic Institute, IRMIA++, Strasbourg University (Laurent Navoret )
9.3 Popularization
9.3.1 Interventions
- 06/2022: Opening conference of the exhibition "Homo Numericus", Shadok, Strasbourg (Laurent Navoret )
- 03/2022: Atelier jeunes lors de l’opération “Ose à la recherche” (organisé par Le Vaisseau et CNRS), Strasbourg, France (Matthieu Boileau )
- 03/2022: Conférence au Collège Sébastien Brant d’Eschau dans le cadre de la semaine des mathématiques, Eschau, France (Matthieu Boileau )
- 2022: participation to an article and AI and numerical simulation in "chut! magazine".
10 Scientific production
10.1 Major publications
- 1 articleA neural network closure for the Euler-Poisson system based on kinetic simulations.Kinetic and Related Models 2021
- 2 articleVectorial kinetic relaxation model with central velocity. Application to implicit relaxations schemes.Communications in Computational Physics274April 2020
10.2 Publications of the year
International journals
National peer-reviewed Conferences
Scientific book chapters
Reports & preprints
10.3 Cited publications
- 21 inproceedingsA local time-stepping Discontinuous Galerkin algorithm for the MHD system.Modélisation et Simulation de Fluides Complexes - CEMRACS 2008Marseille, FranceJuly 2009
- 22 articleOn the role of involutions in the discontinous Galerkin discretization of Maxwell and magnetohydrodynamic systems.IMA Vol. Math. Appl.1422006, 69–88
- 23 inproceedingsResolution of the Vlasov-Maxwell system by PIC Discontinuous Galerkin method on GPU with OpenCL.CEMRACS'1138FranceEDP Sciences2011, 257--274
- 24 articleTwo-Scale Macro-Micro decomposition of the Vlasov equation with a strong magnetic field.Mathematical Models and Methods in Applied Sciences23082013, 1527--1559
- 25 article Long time simulation of a beam in a periodic focusing channel via a two-scale PIC-method.Mathematical Models and Methods in Applied Sciences192ACM 82D10 35B27 76X052009, 175-197URL: http://hal.archives-ouvertes.fr/hal-00180700/en/
- 26 articleStrong stability-preserving high-order time discretization methods.SIAM Rev.4312001, 89--112
- 27 articleA drift-kinetic Semi-Lagrangian 4D Vlasov code for ion turbulence simulation.J. of Comput. Phys. 2172006, 395
- 28 articleConvex Duality and Entropy-Based Moment Closures: Characterizing Degenerate Densities.SIAM J. Control Optim.472008, 1977–2015
- 29 articleEntropy-based moment closures for kinetic equations. Transport Theory Statist. Phys.264-51997, 591–606
- 30 articleThe semi-Lagrangian method for the numerical resolution of the Vlasov equation.J. Comput. Phys.14921999, 201--220
- 31 incollectionEntropy conservative finite element schemes.Numerical methods for Compressible Flows, Finite Difference Element and Volume TechniquesProc. Winter Annual Meeting, Amer. Soc. Mech. Eng, AMD- Vol. 781986, 149

