2024Activity reportProject-TeamSERENA
RNSR: 201521772E- Research center Inria Paris Centre
- In partnership with:Ecole Nationale des Ponts et Chaussées
- Team name: Simulation for the Environment: Reliable and Efficient Numerical Algorithms
- In collaboration with:Centre d'Enseignement et de Recherche en Mathématiques et Calcul Scientifique (CERMICS)
- Domain:Digital Health, Biology and Earth
- Theme:Earth, Environmental and Energy Sciences
Keywords
Computer Science and Digital Science
- A2.1.3. Object-oriented programming
- A2.1.4. Functional programming
- A2.4.3. Proofs
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.5. Numerical Linear Algebra
- A6.2.8. Computational geometry and meshes
- A6.3.1. Inverse problems
- A6.3.4. Model reduction
- A6.3.5. Uncertainty Quantification
Other Research Topics and Application Domains
- B3.1. Sustainable development
- B3.3.1. Earth and subsoil
- B3.4.2. Industrial risks and waste
- B3.4.3. Pollution
- B4.1. Fossile energy production (oil, gas)
- B4.2.1. Fission
- B5.5. Materials
1 Team members, visitors, external collaborators
Research Scientists
- Martin Vohralík [Team leader, INRIA, Senior Researcher, HDR]
- François Clement [INRIA, Researcher]
- Zhaonan Dong [INRIA, Researcher]
- Alexandre Ern [Ecole des Ponts (ParisTech), Senior Researcher, HDR]
- Jean-Charles Gilbert [INRIA, Emeritus]
- Jean-Luc Guermond [UNIV TEXAS AUSTIN, Chair, until Mar 2024, HDR]
- Michel Kern [INRIA, Researcher]
- Géraldine Pichot [INRIA, Researcher]
Faculty Members
- Brahim Amaziane [UPPA, Associate Professor Delegation, from Feb 2024 until Jul 2024, HDR]
- Pierre Rousselin [UNIV PARIS XIII, Professor Delegation, until Aug 2024]
Post-Doctoral Fellows
- Akram Beni Hamad [INRIA, Post-Doctoral Fellow, until May 2024]
- Divay Garg [INRIA, Post-Doctoral Fellow, from Dec 2024]
- Rekha Khot [INRIA, Post-Doctoral Fellow]
PhD Students
- Nicolas Hugot [CEA]
- Abbas Kabalan [ENPC]
- Clément Maradei [INRIA]
- Romain Mottier [ENPC]
- Houda Mouhcine [UPS]
- Baptiste Plaquevent-Jourdain [INRIA]
- Ari Rappaport [INRIA, until Mar 2024]
- Zuodong Wang [INRIA]
- Daniel Zegarra Vasquez [INRIA]
Technical Staff
- Simon Legrand [INRIA, Engineer]
- Raphaël Zanella [INRIA, Engineer, until Sep 2024]
Interns and Apprentices
- Dorian Nicou [INRIA, Intern, from Apr 2024 until Sep 2024]
- Tall Ouba [SORBONNE UNIVERSITE, Intern, from Jun 2024 until Jul 2024]
Administrative Assistant
- Derya Gok [INRIA]
Visiting Scientist
- Jean-Pierre Dussault [UNIV SHERBROOKE, from Mar 2024 until Mar 2024]
External Collaborators
- Guy Chavent [retired]
- François Delebecque [retired]
- Sebastien Furic [auto-entrepreneur]
- Jérôme Jaffré [retired, HDR]
- Caroline Japhet [UNIV PARIS XIII]
- Habib Jreige [SciWorks]
- Vincent Martin [UTC]
- Jean Roberts [retired, HDR]
- Pierre Weiss [retired]
- Lina Zhao [City University of Hong Kong]
2 Overall objectives
The project-team SERENA is concerned with numerical methods for environmental problems. The main topics are the conception and analysis of models based on partial differential equations, the study of their precise and efficient numerical approximation, and implementation issues with special concern for reliability and correctness of programs. We are in particular interested in guaranteeing the quality of the overall simulation process.
3 Research program
3.1 PDE level
Within our project, we start from the conception and analysis of models based on partial differential equations (PDEs). We namely address the question of coupling of different models, such as simultaneous fluid flow in a discrete network of two-dimensional fractures and in the surrounding three-dimensional porous medium, or interaction of a (compressible) flow with the surrounding elastic deformable structure. The key physical characteristics need to be captured, whereas existence, uniqueness, and continuous dependence on the data are minimal analytic requirements that we seek to satisfy. We are also interested in localization, approximation, and model reduction.
3.2 Advanced numerical discretization methods
We consequently design numerical methods for the devised model, while focusing on enabling general polytopal meshes, in particular in response to a high demand from our industrial partners (namely EDF, CEA, and IFP Energies Nouvelles). We in particular promote structure-preserving approaches that mimic at the discrete level the fundamental properties of the underlying PDEs, such as conservation principles and preservation of invariants. We perform numerical analysis in particular in singularly perturbed, unsteady, and nonlinear cases (reaction–diffusion and wave problems, eigenvalue problems, interface problems, variational inequalities, contact problems, degenerate parabolic equations), we apply these methods to challenging problems from fluid and solid mechanics involving large deformations, plasticity, and phase appearance and disappearance, and we develop a comprehensive software implementing them.
3.3 Iterative linearization, domain decomposition, and multigrid solvers
We next concentrate an intensive effort on the development and analysis of efficient solvers for the systems of nonlinear algebraic equations that result from the above discretizations. We work on iterative linearization schemes and analysis. We place a particular emphasis on parallelization achieved via the domain decomposition method, including the space-time parallelization for time-dependent problems. This allows the use of different time steps in different parts of the computational domain, particularly useful in our applications where evolution speed varies significantly from one part of the computational domain to another. We have also recently devised novel geometric multigrid solvers with the contraction factor independent of the approximation polynomial degree. The solver itself is adaptively steered at each execution step by an a posteriori error estimate giving a two-sided control of the algebraic error.
3.4 Optimization, complementarity, nonsmooth analysis, discrete geometry
We dedicate a specific effort to solvers of algebraic inequalities in complementarity form. A rather general mathematical formulation of a complementarity problem reads: find a point such that , , and for all , or, equivalently,
Here, and are smooth functions, the inequalities are understood componentwise, and “” denotes perpendicularity with respect to the Euclidean scalar product. The orthogonality conditions highlight the combinatorial aspect of the problem: there are ways of realizing them. Determining whether a linear complementarity problem (i.e., and are afine) with integer data has a rational solution, let alone calculating one, is NP complete.
Complementarity is used to mathematically formulate systems in which one model among several is active at a given place and time (the index above); hence, the active model ( or ) is an unknown of the problem. They generalize the first-order optimality conditions of an optimization problem, in which complementarity occurs between the inequality constraints and their optimal multipliers. Examples of applications are found in nonsmooth mechanics and dynamics, to model the phase transition problem in multiphase flows, precipitation-dissolution problems in chemistry, portfolio management in finance, computer graphics, meteorology, or economic equilibrium to mention a few. These problems can be refomulated as (usually) nonsmooth equations, which partly motivates our interest in nonsmooth analysis.
3.5 Reliability by a posteriori error control
The fifth part of our theoretical efforts goes towards assessing the precision of the results obtained at the end of the numerical simulation. Here a key ingredient is the development of rigorous a posteriori estimates that make it possible to estimate in a fully computable way the error between the unknown exact solution and its numerical approximation. Our estimates also allow to distinguish the different components of the overall error, namely the errors coming from modeling, the discretization scheme, the nonlinear (Picard, Newton) solver, and the linear algebraic (domain decomposition, multigrid) solver. A new concept here is that of local stopping criteria, where all the error components are balanced locally within each computational mesh element. This naturally connects all parts of the numerical simulation process and gives rise to novel fully adaptive algorithms. We derive a guaranteed error reduction factor at each adaptive loop iteration in model cases together with cost-optimality in the sense that, up to a generic constant, the smallest possible computational effort to achieve the given accuracy is needed. With patchwise techniques, we also achieve mass balance at each iteration step, a highly demanded feature in most of the target applications.
3.6 Safe and correct programming
Finally, we concentrate on the issue of computer implementation of scientific computing programs, noting that precise numerical simulation and guaranteed error estimation are impossible without correct computer implementation. With their increasing complexity, it becomes a major challenge to implement up-to-date scientific computing algorithms using traditional methods and languages. Fortunately, the computer science community has already encountered similar issues, and offers theoretically sound tools for safe and correct programming. We use these tools to design generic solutions for the implementation of the class of scientific computing software the project-team is dealing with. Our focus ranges from high-level programming with OCaml for the precious safety guards provided by its type system and for its ability to encourage functional programming, to proofs of correctness of numerical algorithms and programs, including bounds of the round-off errors, via mechanical proofs with Coq.
[colback=black!5!white] The ultimate objective of the SERENA project-team is to design numerical algorithms that enable to certify the reliability of the overall simulation process and its efficiency with respect to computational resources for the targeted environmental applications.
4 Application domains
4.1 Multiphase flows and transport of contaminants in the subsurface
- fractured and porous media
- flow in large-scale discrete fracture networks
- subsurface depollution after chemical leakage
- nuclear waste disposal in deep underground repositories
- geological sequestration of CO2
- production of oil and gas
4.2 Industrial risks in energy production
- structural mechanics (friction, contact, large deformation, plasticity), mainly related to nuclear reactor operation and safety analysis
- Stokes and Navier–Stokes flows, mainly related to nuclear reactor operation
- seismic wave propagation for detection and protection
- acoustic wave propagation for non destructive evaluation
- electromagnetism for interfaces between dielectrics and negative metamaterials
5 Social and environmental responsibility
5.1 Impact of research results
Via applications with our industrial and environmental partners EDF, CEA, IFP Energies Nouvelles, ANDRA, ITASCA, and BRGM.
6 Highlights of the year
- Alexandre Ern was appointed co-Editor in Chief of IMA Journal of Numerical Analysis as of 01/01/24
7 New software, platforms, open data
7.1 New software
7.1.1 DiSk++
-
Name:
Discontinuous Skeletal C++ Library
-
Keywords:
High order methods, Polyhedral meshes, C++
-
Scientific Description:
Discontinuous Skeletal methods approximate the solution of boundary-value problems by attaching discrete unknowns to mesh faces (hence the term skeletal) while allowing these discrete unknowns to be chosen independently on each mesh face (hence the term discontinuous). Cell-based unknowns, which can be eliminated locally by a Schur complement technique (also known as static condensation), are also used in the formulation. Salient examples of high-order Discontinuous Skeletal methods are Hybridizable Discontinuous Galerkin methods and the recently-devised Hybrid High-Order methods. Some major benefits of Discontinuous Skeletal methods are that their construction is dimension-independent and that they offer the possibility to use general meshes with polytopal cells and non-matching interfaces. The mathematical flexibility of Discontinuous Skeletal methods can be efficiently replicated in a numerical software: by using generic programming, the DiSk++ library offers an environment to allow a programmer to code mathematical problems in a way completely decoupled from the mesh dimension and the cell shape.
-
Functional Description:
The software provides a numerical core to discretize partial differential equations arising from the engineering sciences (mechanical, thermal, diffusion). The discretization is based on the "Hybrid high-order" or "Discontinuous Skeletal" methods, which use as principal unknowns polynomials of arbitrary degree on each face of the mesh. An important feature of these methods is that they make it possible to treat general meshes composed of polyhedral cells. The DiSk ++ library, using generic programming techniques, makes it possible to write a code for a mathematical problem independently of the mesh. When a user writes the code for his problem using the basic operations offered by DiSk ++, that code can be executed without modifications on all types of mesh already supported by the library and those that will be added in the future.
- URL:
- Publication:
-
Contact:
Matteo Cicuttin
-
Partner:
CERMICS
7.1.2 APS-MG
-
Name:
A-Posteriori-Steered MultiGrid
-
Keywords:
Finite element modelling, Linear system, A posteriori error estimates, Multigrid methods, P-robustness
-
Scientific Description:
APS-MG (a-posteriori-steered multigrid) is a geometric-type multigrid solver whose execution is steered by the associated a posteriori estimate of the algebraic error. In particular, the descent direction and the level-wise step sizes are adaptively optimized. APS-MG corresponds to a V-cycle geometric multigrid with zero pre- and solely one post-smoothing step, via block-Jacobi (overlapping additive Schwarz/local patchwise problems). Its particularity is that it is robust with respect to the polynomial degree p of the underlying finite element discretization, i.e., APS-MG contracts the error on each iteration by a factor that is independent of p. APS-MG is the implementation of the solver developed in https://hal.science/hal-02070981 and https://hal.science/hal-02494538.
-
Functional Description:
APS-MG (a-posteriori-steered multigrid) is an iterative linear solver implemented in MATLAB. It can treat systems of linear algebraic equations arising from order p conforming finite element discretization of second-order elliptic diffusion problems. APS-MG is a geometric-type multigrid method and uses a hierarchy of nested meshes. It corresponds to a V-cycle geometric multigrid solver with zero pre- and one post-smoothing step via block-Jacobi (overlapping additive Schwarz/local patchwise problems). A salient feature is the choice of the optimal step size for the descent direction on each mesh level.
- URL:
- Publications:
-
Contact:
Jan Papez
7.1.3 FEMLAB
-
Name:
FEMLAB
-
Keywords:
High order finite elements, Discontinuous Galerkin, Hybrid high-order methods, Adaptive algorithms, Finite element modelling
-
Functional Description:
FEMLAB is a Matlab library for different classes of FEM code. This library is designed to use a parallel computing toolbox in Matlab to accelerate the time for assembling the linear systems. It has been tested on 48 parallel processors of the HPC nodes. Another critical point is that different FEM codes in this library are designed to support arbitrary order of the basis functions and support the adaptive mesh refinement algorithm.
-
Release Contributions:
FEMLAB is updated in 2023 to support the adaptive algorithm.
- URL:
- Publications:
-
Contact:
Zhaonan Dong
7.1.4 coq-num-analysis
-
Name:
Numerical analysis Coq library
-
Keywords:
Formal methods, Coq, Numerical analysis, Finite element modelling
-
Scientific Description:
These Coq developments are based on the Coquelicot library for real analysis. Version 1.0 includes the formalization and proof of: (1) the Lax-Milgram theorem, including results from linear algebra, geometry, functional analysis and Hilbert spaces, (2) the Lebesgue integral, including large parts of the measure theory,the building of the Lebesgue measure on real numbers, integration of nonnegative measurable functions with the Beppo Levi (monotone convergence) theorem, Fatou's lemma, the Tonelli theorem, and the Bochner integral with the dominated convergence theorem.
-
Functional Description:
Formal developments and proofs in Coq of numerical analysis problems. The current long-term goal is to formally prove parts of a C++ library implementing the Finite Element Method.
-
News of the Year:
The formalization in Coq of simplicial Lagrange finite elements is complete. This include the formalizations of the definitions and main properties of monomials, their representation using multi-indices, Lagrange polynomials, the vector space of polynomials of given maximum degree (about 6 kloc). This also includes algebraic complements on the formalization of the definitions and main properties of operators on finite families of any type, the specific cases of abelian monoids (sum), vector spaces (linear combination), and affine spaces (affine combination, barycenter, affine mapping), sub-algebraic structures, and basics of finite dimension linear algebra (about 31 kloc). A new version (2.0) of the opam package will be available soon, and a paper will follow.
We have also contributed to the Coquelicot library by adding the algebraic structure of abelian monoid, which is now the base of the hierarchy of canonical structures of the library.
- URL:
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Sylvie Boldo, François Clement, Micaela Mayero, Vincent Martin, Stéphane Aubry, Florian Faissole, Houda Mouhcine, Louise Leclerc
7.1.5 MODFRAC
-
Name:
MODFRAC
-
Keywords:
Meshing, Fracture network, Ellipses, Polygons, Mesher, Mesh
-
Scientific Description:
The meshing methodology is based on a combined frontal-Delaunay approach in a Riemannian context.
-
Functional Description:
The MODFRAC software automatically builds meshes of fracture networks. As an input, it takes a DFN (Discrete Fracture Network) geometric model consisting of ellipses or polygons that have been randomly generated in the tridimensional space while following experimental statistics. It completes this model by first calculating the intersections between fractures, that are straight segments. On each fracture, it computes in turn the intersections between these straight segments, subdividing them into subsegments. It then creates a conforming set of these subsegments, and selects the necessary fractures using a graph structure. It transmits this information to an “indirect” surface mesher, where the tridimensional mesh results from the construction of planar meshes of the parametric domains.
-
News of the Year:
Addition of the ability to update the mesh with a size map. Better management of 1D and 2D constraints imposed on the surface of the cube.
- Publications:
-
Contact:
Geraldine Pichot
-
Participants:
Patrick Laug, Houman Borouchaki, Geraldine Pichot
-
Partner:
Université de Technologie de Troyes
7.1.6 nef-flow-fpm
-
Keywords:
2D, 3D, Porous media, Fracture network, Geophysical flows
-
Scientific Description:
The code is based on the implementation of the mixed hybrid finite element method as detailed in: An efficient numerical model for incompressible two-phase flow in fractured media Hussein Hoteit, Abbas Firoozabadi, Advances in Water Resources 31, 891–905, 2008. https://doi.org/10.1016/j.advwatres.2008.02.004
The model of fractures and the coupling between the porous flow and the flow in the network of fractures is described in: : Modeling Fractures and Barriers as Interfaces for Flow in Porous Media V. Martin, J. Jaffré, J. E. Roberts, SIAM Journal on Scientific Computing, 2005. https://doi.org/10.1137/S1064827503429363
Validation benchmark test from the publication: Inga Berre, et al., Verification benchmarks for single-phase flow in three-dimensional fractured porous media, Advances in Water Resources, Volume 147, 2021. https://doi.org/10.1016/j.advwatres.2020.103759.
-
Functional Description:
nef-flow-fpm is a Matlab code to simulate flows in fractured porous media with the mixed-hybrid finite element methods (RT0).
-
Release Contributions:
Implementation of the mixed hybrid method for 3D porous flows, Discrete fracture Networks (DFN) flows and the coupling between DFN and porous flows.
-
News of the Year:
Validation of the data per subdomain for HPDDM solver (Neumann matrices, local sizes and indices, local second member), add an option to assemble the linear system with the boundary conditions (BCs) and save the necessary data so that the Dirichlet BCs are removed in parallel in PETSc. Simulations with the demonstrator for PETSc/HPDDM, the largest networks contains 696k fractures (and 243M unknowns).
- URL:
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Daniel Zegarra Vasquez, Michel Kern, Raphael Zanella
7.1.7 nef-transport-fpm
-
Keywords:
3D, Porous media, Incompressible flows, Transport model
-
Scientific Description:
The discretization in space is performed with a cell-centered finite volume scheme. The discretization in time can be either explicit or implicit.
Validation benchmark test from the publication: Inga Berre, et al., Verification benchmarks for single-phase flow in three-dimensional fractured porous media, Advances in Water Resources, Volume 147, 2021. https://doi.org/10.1016/j.advwatres.2020.103759.
-
Functional Description:
nef-transport-fpm is a Matlab code for simulating transport by advection diffusion in porous-fractured media.
-
News of the Year:
Add transport in a fractured porous medium with the proper handling of the coupling conditions between the fractures (2D) and the rock matrix (3D) and the coupling conditions at the fractures intersections (1D). Validation of the implementation by comparison with the Field test case described in Inga Berre, et al., 2021 (https://doi.org/10.1016/j.advwatres.2020.103759).
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Michel Kern, Daniel Zegarra Vasquez, Alessandra Marelli, Dania Khiralla
7.1.8 demonstrator-nef-hpddm
-
Keywords:
Fracture network, Geophysical flows, Linear Systems Solver
-
Functional Description:
The demonstrator is a C++ code based on the PETSc (Portable, Extensible Toolkit for Scientific Computation) library which is able to solve the linear system A x= b, where A is an invertible symmetric matrix, x is the unknown vector and b is a given vector. The goal is to solve the linear system assembled by the Matlab finite element code nef-flow-fpm, which is dedicated to the simulation of flows in fractured/porous media, with more performant solvers than those available in Matlab. The linear system in the demonstrator is loaded from binary files (.dat) or assembled from structures loaded from binary files. The binary files are written in nef-flow-fpm with a specific Matlab function available in the PETSc repository (PetscBinaryWrite.m). The solution obtained with the demonstrator may be written in a text file through a PETSc option (-ksp_view_solution), to be latter on loaded in nef-flow-fpm for post-processing.
The solving may be performed in parallel on distributed memory machines thanks to PETSc, which uses MPI functions. Any linear solver and preconditioner available in PETSc may be chosen to solve the linear system. In particular, it is possible to use the preconditioner KSPHPDDM for domain decomposition methods. It is then possible to use Neumann matrices to improve the solving. A Neumann matrix is the matrix obtained for a given subdomain (with overlap) where Neumann boundary conditions are enforced at the interfaces with the other subdomains. The source files of the demonstrator are main.cpp, functions.hpp/cpp and scaling.hpp/cpp.
- URL:
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Raphael Zanella
7.1.9 ParaCirce
-
Name:
Parallel Circulant Embedding
-
Keywords:
2D, 3D, Hydrogeology, Gaussian random fields, MPI
-
Scientific Description:
ParaCirce implements the algorithm proposed by [C. R. Dietrich and G. N. Newsam. A fast and exact method for multidimensional gaussian stochastic simulations. Water Resources Research, 29(8):2861-2869, 1993] as well as an algorithm to accelerate the padding estimation [Pichot et al. SMAI Journal of Computational Mathematics, 8, pp.21, 2022].
-
Functional Description:
ParaCirce implements a parallel Circulant Embedding method for the generation in parallel of 2D or 3D Gaussian Random Fields (second order stationary).
-
Release Contributions:
- Simple precision fields generation support - HDF5 format fields export
-
News of the Year:
- Export fields in HDF5 format - Add simple precision support - WIP: Support of multidimensional communicators
- URL:
- Publication:
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Simon Legrand
7.1.10 Pruners
-
Name:
Pruners
-
Keyword:
Parameter studies
-
Functional Description:
Pruners is a language aimed at automating parameter studies. It allows the specification of parameter combinations, and make them available via environment variables. Those can then be used by any specified command as input parameters.
-
Release Contributions:
- Bug fix: Json arrays support - Bug Fix: Curly brackets aroud variables are properly removes when configuring
-
News of the Year:
- Bug fix: Json arrays support - Bug Fix: Curly brackets aroud variables are properly removes when configuring
- URL:
-
Contact:
Thierry Martinez
7.1.11 Hnm4lcp
-
Name:
Hybrid Newton-Min algorithm for Linear Complementarity Problems
-
Keywords:
Linear complementarity problem, Global convergence, Least-square merit function, Linesearch, Minimum function, Nonsmooth reformulation, P-matrix, Polyhedral Newton-min algorithm, Semismooth Newton
-
Functional Description:
Hnm4lcp solves a linear complementarity problem, which consists in finding a vector x with nonnegative components such that the vector Mx+q (the square matrix M and the vector q are given) is also nonnegative and perpendicular to x. This is denoted by <blockquote> 0 <= x _|_ (Mx+q) >= 0. </blockquote> This type of problem appears in the optimality conditions of a quadratic optimization problem, in nonsmooth mechanics (in robotics in particular), can express dissolution-precipitation phenomena in chemistry, in multiphase flows, in meteorology, etc.
The followed solution approach consists in reformulating the problem in the form of the nonsmooth equation H(x) = 0, where <blockquote> H(x) := min(x,Mx+q) </blockquote> and to apply a kind of semismooth Newton algorithm to it (the used Jacobian belongs to the product B-differential of H). This one is modified to ensure the global convergence of the algorithm, which requires to compute a point in a convex polyhedron at some iterations (rarely, actually).
- URL:
- Publication:
-
Contact:
Jean Charles Gilbert
-
Partner:
Jean-Pierre Dussault, Université de Sherbrooke, Québec, Canada
7.1.12 ISF
-
Name:
Isf and Bdiffmin
-
Keywords:
B-differential, Hyperplane arrangement
-
Scientific Description:
The code is described in the following two reports:- - https://inria.hal.science/hal-04048393 - https://hal.science/hal-04102933
-
Functional Description:
The B-diffrential computed by Bdiffmin is a concept of derivative for a nonsmooth function. The function considered by Bdiffmin is the componentwise minimum of two affine functions: x -> min (Ax+a,Bx+b), where A and B are mxn real matrices, while a and b are real vectors of size m. In this case, the B-differential is a finite (between 1 and 2m̂ éléments) collection of Jacobians (i.e., mxn matrices). The computing time is polynomial per computed Jacobian.
To realize this task, Bdiffmin calls the Matlab function ISF (for Incremental Sign Feasibility), which has been designed to determine the chambers of an arrangement of hyperplanes having a point in common. The sign vectors computed by the latter function can be used to solve a number of other enumeration problems such as - determining the signed feasibility of strict inequality systems, - listing the orthants encountered by the null space of a matrix, - itemizing the pointed cones generated by a set of vectors and their inverses, - giving the bipartitions of a finite set of points that can be separated by an affine hyperplane and many others.
- URL:
- Publications:
-
Contact:
Jean Charles Gilbert
-
Participants:
Jean-Pierre Dussault, Jean Charles Gilbert, Baptiste Plaquevent-Jourdain
7.1.13 ISF_jl
-
Name:
Incremental Sign Feasibility - Julia version
-
Keywords:
Hyperplane arrangement, Combinatorics, Matroids
-
Functional Description:
This code extends the ISF code (in Matlab) to general affine arrangements, while ISF is restricted to linear arrangements. It is written in Julia. Its goal is to list the chambers of a hyperplane arrangement, i.e., to obtain the sign vectors corresponding to each of them. This tool, mainly developed for research purposes, may use several methods. In particular, a "dual" approach using the matroid circuits associated with the arrangement is available.
-
Contact:
Baptiste Plaquevent-Jourdain
8 New results
8.1 Research axis 1: Advanced numerical discretizations and solvers
Participants: Akram Beni Hamad, Zhaonan Dong, Jean-Pierre Dussault, Alexandre Ern, Jean Charles Gilbert, Jean-Luc Guermond, Nicolas Hugot, Michel Kern, Rekha Khot, Clément Maradei, Baptiste Plaquevent-Jourdain, Martin Vohralík, Zuodong Wang.
Invariant-domain time-stepping for compressible flows
Participants: Alexandre Ern, Jean-Luc Guermond, Zuodong Wang.
In 2022, Alexandre Ern and Jean-Luc Guermond laid the foundations of a new paradigm for invariant-domain time-stepping applied to hyperbolic problems using high-order Runge–Kutta methods. The main application in mind are the compressible Navier–Stokes equations. The main contribution this year in this direction is the devising of sectorially A-stable alternating implicit Runge–Kutta schemes of third-order 55. This has been a long-standing barrier for decades, where only second-order accuracy was available together with some form of A-stability.
Moreover, in 25, we considered a scalar conservation law with a stiff source term having multiple equilibrium points. For this quite challenging situation, we proposed a scheme that can be asymptotic-preserving.
Analysis of HHO methods
Participants: Zhaonan Dong, Alexandre Ern, Rekha Khot.
Hybrid high-order (HHO) methods play still an important role in our research endeavors. One contribution 20 is the devising and analysis of a -HHO method for the biharmonic problem. A second one 26 is the fully discrete analysis of the HHO space discretization combined with the explicit leapfrog scheme for the acoustic wave equation in its second-order form. The challenge here was to handle the static coupling between cell and face unknowns. A third contribution 58 is the fully discrete analysis of explicit Runge–Kutta schemes combined with HHO methods for the acoustic wave equation in its first-order form. Two main steps forward are (i) a unified vision of abstract assumptions underlying the error analysis; (ii) a broad appraoch for interpolation operators, encompassing several nown operators from either the HHO or Hybridizable discontinuous Galerkin (HDG) context, thereby providing a further unifying bridge between HHO and HDG.
Stabilized primal-dual method for sign-changing elliptic PDEs
Participants: Alexandre Ern.
Sign-changing elliptic PDEs are encountered in metamaterials leading to propagation of waves in ways that are unknown from naturally ocurring materials. The simplest model is that of a second-order diffusive PDE posed on two sub-domains separated by an interface, with a positive diffusion coefficient in one sub-domain and a negative coefficient in the other. The discretization of such problems is quite challenging. The standard Galerkin discretization is stable only under rather strong assumptions on the mesh, essentially hinging on some symmetry properties that are difficult to satisfy in practice. Our main contribution is a novel discretization method that is stable on general shape-regular meshes that are fitted to the interface. The key idea is to employ a stabilized primal-dual approach. Thus, the price to pay to gain better stability is to solve a saddle-point problem. The numerical analysis along results on challenging problems are reported in 41. Results for the cloaking using a metamaterial are reported in Figure 1; one can see the striking role of the cloak on the right panel.
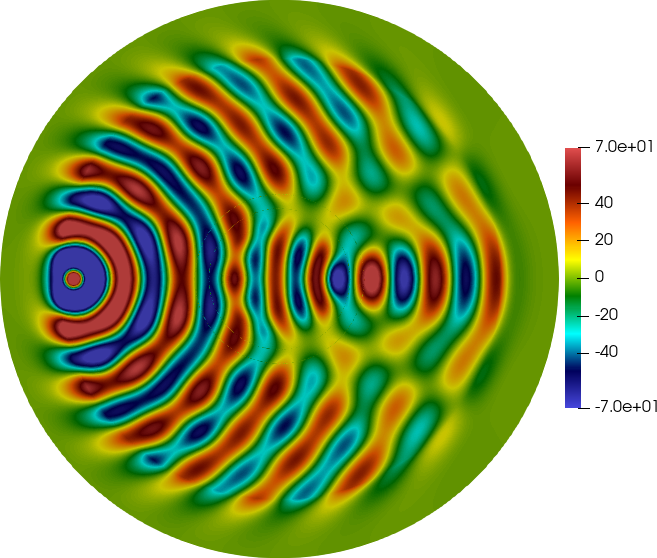
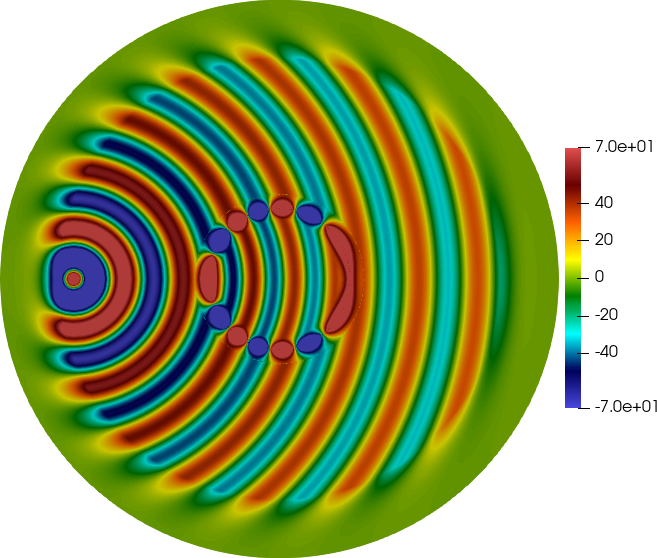
No cloaking vs. cloaking with metamaterial.
No cloaking vs. cloaking with metamaterial.
Multigrid and domain decomposition solvers steered by a posteriori estimates of the algebraic error
Participants: Akram Beni Hamad, Martin Vohralík.
In 38 and 63, we consider iterative algebraic solvers for saddle-point mixed finite element discretizations of arbitrary polynomial degree of the model Darcy flow problem. We propose 1) a posteriori error estimators of the algebraic error; and 2) novel iterative algebraic solvers. The estimators control the algebraic error from above and from below in a guaranteed and fully computable way. The solvers are then steered by these estimators. The distinctive feature of the approaches in both 38 and 63 is that they produce a locally mass conservative approximation on each iteration. This is easier in 63, where a divergence-free approximation is constructed on each iteration of a multigid or an overlapping domain decomposition approach (updating a suitable initial guess), but ingenious in 38, where a nonoverlapping domain decomposition framework is considered. A line search is employed in both cases to determine the optimal step size, leading to a Pythagoras formula for the algebraic error decrease in each iteration. A multilevel stable decomposition of the velocity space is designed in 63 to prove a -robust contraction of the algebraic error on each iteration and, simultaneously, the efficiency of the associated lower algebraic a posteriori estimator. Both approaches are suitable for massive parallelization. Numerical experiments illustrate the theoretical developments. Figure 2 from 38 illustrates a fast convergence for a model problem with repeated diffusion contrast of size , tight computable upper and lower bounds on the algebraic error, and an accurate prediction of the distribution of the algebraic error.
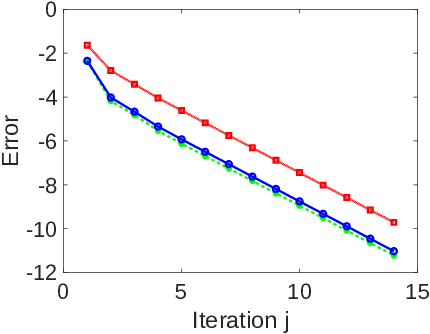
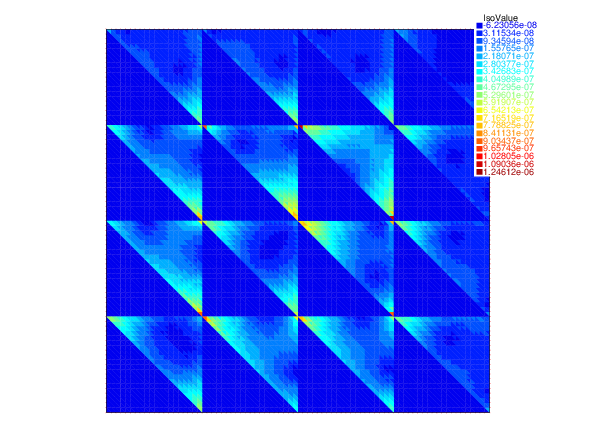
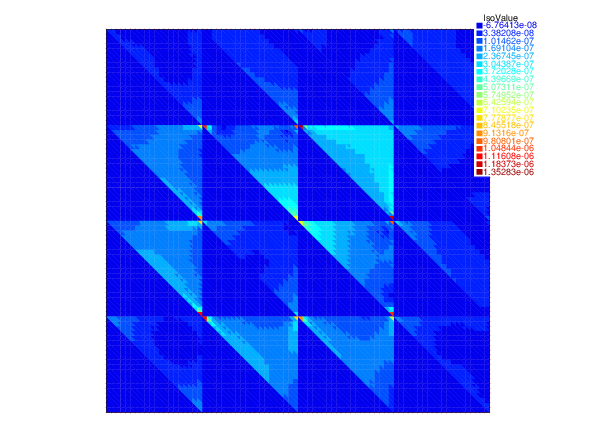
Algebraic errors and estimates
Algebraic errors and estimates
Complementarity problems
Participants: Jean-Pierre Dussault, Jean Charles Gilbert, Baptiste Plaquevent-Jourdain.
The contributions 22, 52 propose new approaches to solve the complementarity problem with some global convergence result (with the Polyhedral Newton-Min or PNM algorithm) and fast local convergence (with a hybrid version, called HNM). The proposed approach reformulates the problem with the Minimum C-function, that is , and takes the associated least-square function as merit function, which means that the progress to the solution is measured by the imposed decrease of . This approach is standard when is smooth, which is not the case here. In the present case, this approach is still very efficient when it works... but many pitfalls must be overcome to get that efficiency. The main difficulty is that the semi-smooth-like Newton direction on may not be a descent direction of . To overcome this dificulty, the semi-smooth-like Newton direction is replaced at some iterations by the computation of a direction in a polyhedron defined by a usually small number of linear inequality constraints (PNM principle). The HNM method has quadratic local convergence when the limit point satisfies some reinforced regularity conditions. Numerical experiments with Hnm4lcp (§ 7.1.11) show the efficiency of the approach for linear complementarity problems (i.e., when and are affine).
The Levenberg-Marquardt approach is a technique that makes possible to have global convergence of Newton-like iterations with much weaker regularity conditions, hence making the convergence more robust. In 67, this approach is applied to the nonsmooth system for the function defined above. With this technique, the PNM principe no longer needs to require that the constructed polyhedra are nonempty. Instead, the algorithm minimizes a function made of convex quadratic pieces, which always has a minimizer, at the price of a higher computational cost. Some complexity issues are also evoked, in relation with geometric considerations close to hyperplane arrangements, which shed some new light on the reformulation of complementarity problems with the minimum C-function. It is shown that detecting strong stationarity of the merit function at a point (i.e., , for all ) is co-NP-complete. Finding a point satisfying a weaker form of stationarity (i.e., ), however, may be feasible under suitable assumptions.
Nonsmooth analysis
Participants: Jean-Pierre Dussault, Jean Charles Gilbert, Baptiste Plaquevent-Jourdain.
The contributions 23, 53 propose an algorithm for computing the B-differential (roughly speaking, the set of Jacobians found at points very near the considered point) of the componentwise minimum of two affine functions, which is the map , where , , , and the minimum function “” acts componentwise. The B-differential of this function is a finite set of that can have a number of elements that is exponential in . Along the way, we identify several equivalent problems in linear algebra, convex analysis and discrete geometry. Several properties of the B-differential, like its symmetry, conditions for its completeness, its connectivity, bounds on its cardinality, etc, are also stated and proved. It is the hyperplane arrangement formulation that is the most appropriate for calculation. With this point of view, we improve significantly an algorithm proposed by Rada and Černy in 2018 (the speed-up can exceed 100, but this one depends much on the considered instance) and propose a dual approach based on Gordan's theorem of the alternative, matroid circuits and the introduced notion of stem vectors. The Matlab code isf (§ 7.1.12) has been developed to validate the proposed algorithms.
Discrete geometry
Participants: Jean-Pierre Dussault, Jean Charles Gilbert, Baptiste Plaquevent-Jourdain.
The hyperplanes in 23, 53 are linear, meaning that they all contain zero. The contribution 68 extends the approach proposed in 23 to affine arrangements, which means that their hyperplanes may not have a point in common. Many properties of affine arrangements are also stated in this more general case and proved with an analytic viewpoint, whilst algebraic tools are most often used to study these problems. The dual point of view is obtained thanks to Motzkin's theorem of the alternative, rather than Gordan's. The Julia code isf_jl (§ 7.1.13) has been written to assess the efficiency of the algorithms proposed to enumerate the chambers of an affine arrangement.
8.2 Research axis 2: A posteriori error control, adaptivity, and safe and correct programming
Participants: François Clément, Alexandre Ern, Sébastien Furic, Houda Mouhcine, Ari Rappaport, Pierre Rousselin, Martin Vohralík.
A posteriori error estimates for the wave equation
Participants: Zhaonan Dong, Alexandre Ern, Zuodong Wang.
A posteriori error estimates for the wave equation are quite challenging (in particular, because of the lack of a well established inf-sup stability framework), and results in the literature are still quite scarce. In 44, we considered damped energy-norm error estimates and were able to establish both upper and lower bounds on the error, up to some higher-order terms, under the assumptions of smooth enough and compactly supported sources away from the origin.
A posteriori error estimates for the DG-CG time-stepping method combined with the finite element method (FEM) in space, applied to the wave equation, are presented in 51. These estimates are formulated in the -norm, providing a constant-free upper bound that is optimal with respect to both the mesh size and the polynomial degree.
A posteriori error estimates and adaptivity for nonsmooth problems
Participants: Ari Rappaport, Martin Vohralík.
In 28, we develop guaranteed a posteriori error estimates for nonlinear problems with nonsmooth nonlinearities and design adaptive regularization algorithms that automatically apply only the amount of regularization necessary not to harm the overall precision. This makes the Newton method converge in situations where it would fail usually and enables to keep long time steps for evolutive problems. In 27, we apply this approach to the doubly-degenerate Richards equation (a central model for saturated-unsaturated flows in porous media). Figure 3 presents the instantaneous computational gains, where the “no harm of the overall precision” is presented graphically. These results were obtained in the Ph.D. thesis of Ari Rappaport 37 defended this year.
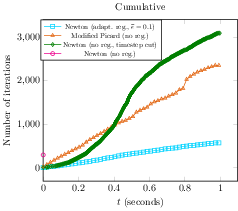

A posteriori error estimates and adaptivity for nonsmooth problems
A posteriori error estimates and adaptivity for nonsmooth problems
Coq formalizations
Participants: François Clément, Houda Mouhcine, Pierre Rousselin.
In 45, we provide very detailed pen-and-paper proofs for the construction of the Lagrange finite elements of any degree on simplicies in positive dimension. The first version of the document covers: the general definition of finite element, the construction of simplicial Lagrange finite elements on a segment including results about Lagrange polynomials, and the construction of simplicial Lagrange finite elements in dimension including the construction of multi-indices of given maximum length, results about multivariate polynomials such as the linear independence of monomials and the Euclidean division by a monomial, results about Lagrange polynomials such as their view as barycentric coordinates, results about affine geometric mappings such as the transformation of -faces of dimension , results about Lagrange nodes and Lagrange linear forms of , and the proofs of unisolvence of , and of face unisolvence.
These detailed proofs served as a guideline for the formalization in Coq of the simplicial Lagrange finite elements during the Ph.D. thesis of Houda Mouhcine 36 defended this year. See also the "News of the Year" about software coq-num-analysis (Section 7.1.4).
In the context of the Inria Challenge LiberAbaci, and during the half-delegation of Pierre Rousselin in the project-team SERENA, two papers were presented at the 13th international workshop on Theorem proving components for Educational software (ThEdu'24). In 34, we present worksheets in Coq for students to learn about divisibility and binomial coefficients. Technical and pedagogical choices are presented, as well as numerous exercises. In 35, we report on a 3-year teaching experiment conducted at Sorbonne Paris Nord University. The subject was an introductory course in formal proofs with the Coq proof assistant given to first-year students in a double major mathematics and computer science curriculum. Practical session worksheets are presented, and the evolution of the course and improvements in both technical and pedagogical aspects are discussed.
8.3 Research axis 3: Applications to environment and energy
Participants: Alexandre Ern, Abbas Kabalan, Michel Kern, Simon Legrand, Clément Maradei, Romain Mottier, Dorian Nicou, Tall Ouba, Géraldine Pichot, Martin Vohralík, Raphaël Zanella, Daniel Zegarra Vasquez.
Flow through fractured and fractured porous media
Participants: Michel Kern, Simon Legrand, Tall Ouba, Géraldine Pichot, Raphaël Zanella, Daniel Zegarra Vasquez.
We have continued the work with the domain decomposition preconditioner HPDDM, developped by the Alpines team 69, 70 to solve the linear system obtained from nef-flow-fpm(§ 7.1.6). We demonstrate that HPDDM outperforms other more classical preconditioners used until then (mainly algebraic multigrid) as can be seen on Figure 4.
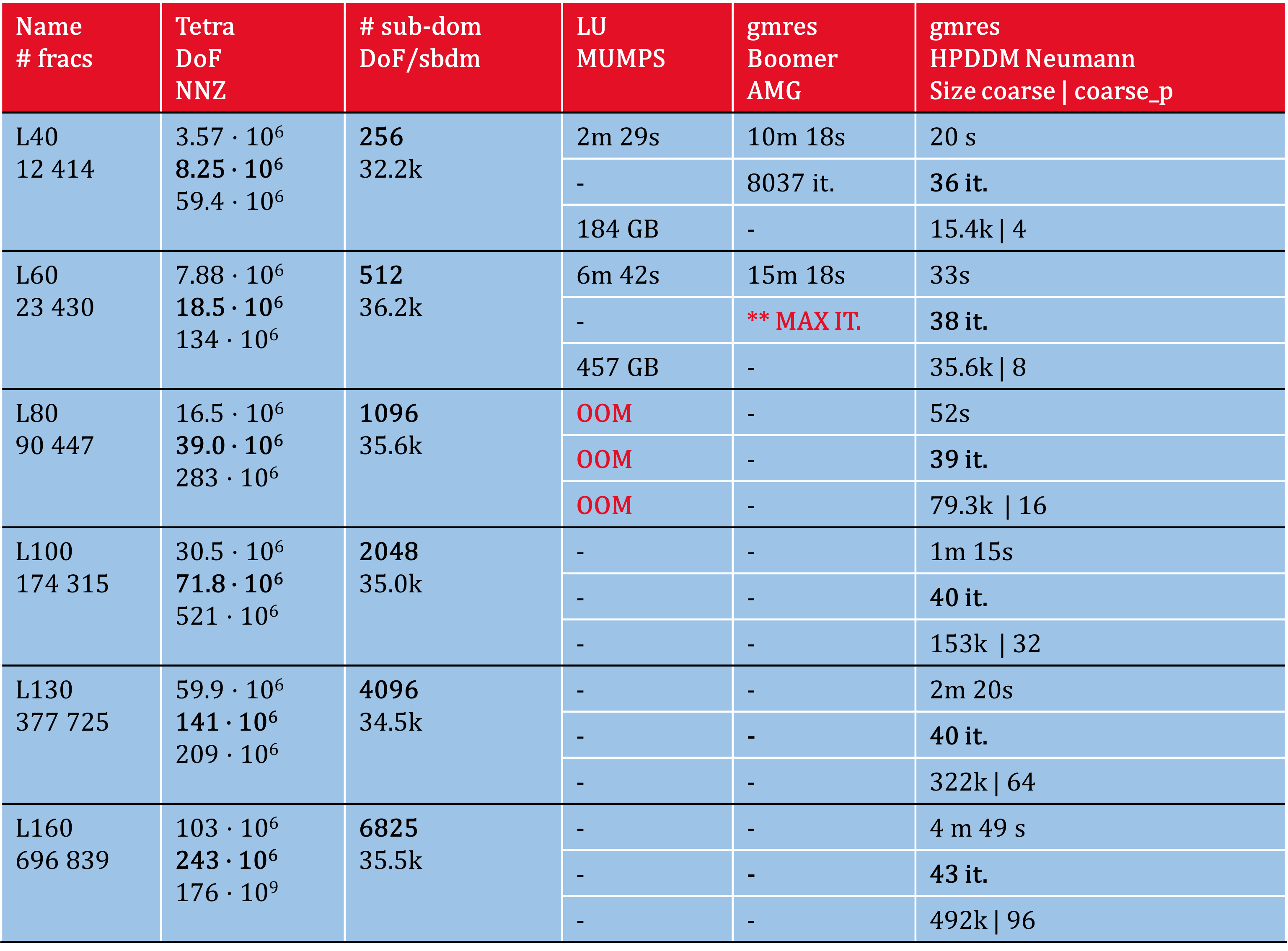
Performances of the domain decomposition preconditioner HPDDM
Thanks to the GMRES solver and the HPDDM preconditioner, we are now able to solve flow problem in large scale fractured porous media that are out of reach with direct solvers like MUMPS Cholesky or with GMRES preconditioned by multigrid like BoomerAMG. As an example, solving the linear system of size for a network containing 696k fractures takes only 4 minutes and 49 iterations in parallel with 6825 MPI processes, using GMRES preconditioned with HPDDM. The simulations are run on the TGCC (GENCI / CEA).
Another goal is to simulate the transport by advection of an inert tracer. The transport is described by the conservation of mass and gives rise to an equation with partial derivatives of the first order in which the velocity, computed with the software nef-flow-fpm(§ 7.1.6), is heterogeneous. The discretization in space is performed with a cell-centered finite volume scheme. The discretization in time can be either explicit or implicit.
As part of Tall Ouba 's internship, we are now able to simulate the transport in a fractured porous medium. The main challenge was the correct handling of the coupling conditions between the rock and the fractures . An example is shown in Figure 5. The method is implemented in nef-transport-fpm(§ 7.1.7).
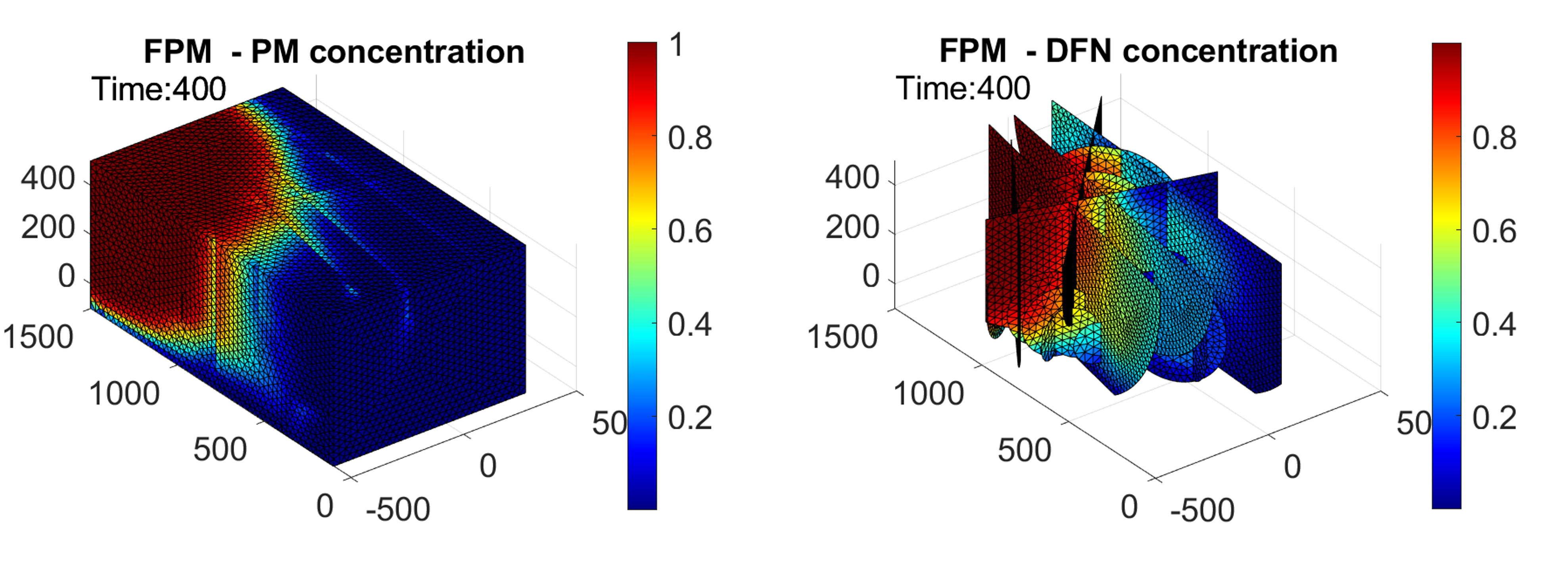
Concentration in the porous medium and in the discrete fracture network with 52 fractures.
Multiphase flow
Participants: Michel Kern, Brahim Amaziane, Dorian Nicou.
Michel Kern was part of a group with Etienne Ahusborde, Brahim Amaziane (University of Pau), Stephen de Hoop and Denis Voskov (Delft University of Technology) that proposed a benchmark targeted towards the simulation of reactive two-phase flow. Six teams participated in the benchmark. The results showed good agreements between most groups on the simpler test cases, but also that the interaction between complex chemistry and two-phase flow with phase exchanges still remains a challenge for simulation software. The model is presented in 30, while the results are presented in 14, see Figure 6.

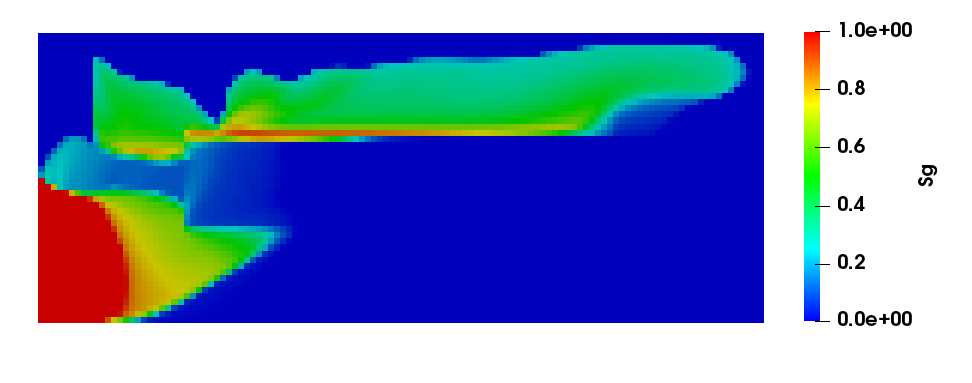
Evolution of the gas saturation
Evolution of the gas saturation
Etienne Ahusborde (Université de Pau) and Michel Kern formed a team that participated in The 11th Society of Petroleum Engineers. Comparative Solution Project. The goal was to compare simulation codes for CO2 sequestration on realistic test cases. Our teams presented results for all three test cases that were in line with the majority of other groups, see Figure 7. A synthesis article is in preparation.


CO2 molar fraction ,SPE CSP tcase B
CO2 molar fraction ,SPE CSP tcase B
Wave propagation in geophysical media
Participants: Alexandre Ern, Romain Mottier.
Within the Ph.D. thesis of Romain Mottier (to be submitted soon), we developed HHO methods to simulate coupled acoustic-elastodynamic waves in geophysical media. One goal is to highlight the role of sedimentary bassins in energy transfer from the bedrock to the atmosphere. An illustration is shown in Figure 8.

Wave propagation in a sedimentary bassin.
Data assimilation
Participants: Alexandre Ern.
Our work on data assimilation was pursued this year by addressing the wave equation. Our main contribution deals with the devising and numerical analysis of a high-order method (based on a dG method in time and a hybrid dG method in space) 40. The step forward with respect to our previous work on the heat equation is that the conditional stability of the wave equation is more delicate. Moreover, the stabilization strategy had to be revised in order to cope with the higher-order time derivatives.
8.4 Research axis 4: PDE and numerical analysis foundations
Participants: Zhaonan Dong, Alexandre Ern, Jean-Luc Guermond, Géraldine Pichot, Martin Vohralík.
A stable local commuting projector and optimal approximation estimates in
Participants: Théophile Chaumont-Frelet, Martin Vohralík.
In 18, we design an operator from the infinite-dimensional Sobolev space to its finite-dimensional subspace formed by the Nédélec piecewise polynomials on a tetrahedral mesh that has the following properties: 1) it is defined over the entire , including boundary conditions imposed on a part of the boundary; 2) it is defined locally in a neighborhood of each mesh element; 3) it is based on simple piecewise polynomial projections; 4) it is stable in the -norm, up to data oscillation; 5) it has optimal (local-best) approximation properties; 6) it satisfies the commuting property with its sibling operator on ; 7) it is a projector, i.e., it leaves intact objects that are already in the Nédélec piecewise polynomial space. This operator can be used in various parts of numerical analysis related to the space. We in particular employ it here to establish the two following results: i) equivalence of global-best, tangential-trace- and curl-constrained, and local-best, unconstrained approximations in including data oscillation terms; and ii) fully - and - (mesh-size- and polynomial-degree-) optimal approximation bounds valid under the minimal Sobolev regularity only requested elementwise.
Maxwell's equations
Participants: Alexandre Ern, Jean-Luc Guermond.
In 43, we established the asymptotic optimality of the edge finite element approximation of the time-harmonic Maxwell's equations. This fundamental result, which is the counterpart of a known result concering the Helmholtz equation and conforming finite elements, was still lacking in the litterature. As a further development, we also established in 42 a similar result for the discontinuous Galerkin approximation, this time involving an additional high-order perturbation related to the approximated flux. Additionally, we devised a novel residual-based a posteriori error analysis for the Maxwell problem in the frequency domain.
A second novel result, that was also lacking in the literature, concerns the spectral correctness (no spurious eigenvalues) of the dG approximation of Maxwell's equations in first-order form (the result was known for Maxwell's equations in second-order form), thereby confirming numerical observations by various authors made over the last two decades. We proved this result with constant coefficients last year, and generalized it to the case of variable coefficients in 24. The analysis is quite challenging, and relies upon a duality argument and a deflated inf-sup condition. As a further extension, we showed in 54 that the same results holds for a continuus finite element discretization combined with edge stabilization on special meshes (for instance, based on Alfeld splits of given simplicial meshes).
Solutions to 1D advection-diffusion problems with discontinuous coefficients
Participants: Géraldine Pichot.
Diffusive transport in media with discontinuous properties is a challenging problem that arises in many applications. In 15, we focus on one-dimensional discontinuous media with generalized permeable boundary conditions at the discontinuity interface. The paper presents novel analytical expressions from the method of images to simulate diffusive processes, such as mass or thermal transport. The analytical expressions are used to formulate a generalization of the existing Skew Brownian Motion, HYMLA and Uffink's method, here named as GSBM, GHYMLA, and GUM respectively, to handle generic interface conditions. The algorithms rely upon the random walk method and are tested by simulating transport in a bimaterial and in a multilayered medium with piecewise constant properties. The results indicate that the GUM algorithm provides the best performance in terms of accuracy and computational cost. The methods proposed can be applied for simulation of a wide range of differential problems, like heat transport problem 16.
Model-order reduction
Participants: Alexandre Ern, Abbas Kabalan.
One important topic has been the development of reduced-order methods to handle variational inequalities such as those encountered when studying contact problems (with friction) in computational mechanics. In 32, we introduce a new approach in the reduced-order modeling context, where the constraints are taken into account by a nonlinaer Nitsche's method, thereby allowing one to use a primal formulation. Another important topic, explored within the Ph.D. thesis of Abbas Kabalan , is the construction of morphings between a reference shape and a collection of target shapes. The main achievement is to devise an efficient version of the approach based on an offline/online decomposition. The approach can also be used to learn scalar outputs on variable geometries. The methodology and associated numerical results are reported in 62.
-optimal error estimates for nonconforming methods
Participants: Zhaonan Dong, Alexandre Ern.
In 48, we derived -a posteriori error estimates for the HHO method applied to a variable-diffusion problem. The main breakthrough is the use of local Helmholtz decompositions combined with a partition-of-unity technique to bound the nonconformity error. Novel insights were also gained by leveraging the conservative property of HHO methods and exploiting equilibrated fluxes in the derivation of the error upper bound.
Moreover, recently, we derived -optimal error estimates for the upwind dG method when approximating solutions to first-order hyperbolic problems with constant convection fields in the and DG norms in 21. The main novelty in the analysis are novel -optimal approximation properties of the special projector introduced in [Cockburn, Dong, Guzmán, SINUM, 2008]. These works were performed in collaboration with L. Mascotto.
A hypocoercivity-exploiting stabilised finite element method for Kolmogorov equation
Participants: Zhaonan Dong.
In 50, we propose a new stabilised FEM for the Kolmogorov equation. The latter serves as a basic model problem for large classes of kinetic-type equations and, crucially, is characterised by degenerate diffusion. The stabilisation is constructed so that the resulting method admits a numerical hypocoercivity property, analogous to the corresponding property of the PDE problem. More specifically, the stabilisation is constructed so that spectral gap is possible in the resulting “stronger-than-energy” stabilisation norm, despite the degenerate nature of the diffusion in Kolmogorov, thereby the method has a provably robust behaviour as the “time” variable goes to infinity, see Figure 9 for an illustration. We consider both a spatially discrete version of the stabilised finite element method and a fully discrete version, with the time discretisation realised by discontinuous Galerkin timestepping. Both stability and a priori error bounds are proven in all cases. Numerical experiments verify the theoretical findings. These works were performed in collaboration with P. Herbert and E. H. Georgoulis.
Kolmogorov decay to equilibrium
Kolmogorov decay to equilibrium
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
Participants: Alexandre Ern, Martin Vohralík.
- Two-part contract with CEA accompanying the PhD thesis of Nicolas Hugot.
- Two-part contract with Safran Tech accompanying the PhD thesis of Abbas Kabalan (co-supervised with V. Ehrlacher).
- Two-part contract with CEA accompanying the PhD thesis of Romain Mottier.
- Two-part contract with ANDRA accompanying the PhD thesis of Ari Rappaport.
10 Partnerships and cooperations
10.1 International research visitors
10.1.1 Visits of international scientists
Inria International Chair
The INRIA International Chair of Jean-Luc Guermond (Prof. at Texas A&M University) came to an end in March 2024 after five years of collaboration. The main highlights in 2024 are the proof of spectral correctness of the discontinuous Galerkin approximation of the Maxwell eigenvalue problem in first-order form, and the devising of a novel, third-order, alternating implicit Runge–Kutta time integrator.
Other international visits to the team
Jean-Pierre Dussault
-
Status
(Associate professor)
-
Institution of origin:
Université de Sherbrooke
-
Country:
Canada
-
Dates:
4/3/2024 to 22/3/2024
-
Context of the visit:
Jean-Pierre Dussault co-supervises the Ph.D. thesis of Baptiste Plaquevent-Jourdain. His visit was in the framework of this supervision, as well as to conclude the revision of a joint paper on complementarity problems (52) and to undertake new projects.
-
Mobility program/type of mobility:
(invited professor)
Martin Licht
-
Status
(Bernoulli Instructor)
-
Institution of origin:
EPFL Lausanne
-
Country:
Switzerland
-
Dates:
23/04/2024 to 26/04/2024
-
Context of the visit:
Martin Licht visited the SERENA team to give a seminar and to discuss with Martin Vohralík about computable constants for Poincaré–Friedrichs inequalities.
-
Mobility program/type of mobility:
(research stay)
Lorenzo Mascotto
-
Status
(Associate professor)
-
Institution of origin:
University of Milano-Bicocca
-
Country:
Italy
-
Dates:
17/08/2024 to 24/08/2024
-
Context of the visit:
Dr L. Mascotto (University of Milano-Bicocca) visited the SERENA team for a week in August 2024. He mainly interacted with Zhaonan Dong on a posteriori error estimate for DG-CG method for wave equation.
-
Mobility program/type of mobility:
(research stay)
Lina Zhao
-
Status
(Assistant professor)
-
Institution of origin:
City University of Hong Kong
-
Country:
China
-
Dates:
01/12/2024 to 18/12/2024
-
Context of the visit:
Dr. L. Zhao (City University of Hong Kong) visited the SERENA team for 2 weeks in December 2024. She mainly interacted with Zhaonan Dong on a posteriori error analysis for the Stokes–Darcy coupled flow.
-
Mobility program/type of mobility:
(research stay)
10.1.2 Visits to international teams
Research stays abroad
Martin Vohralík
-
Visited institution:
Charles University
-
Country:
Czech Republic
-
Dates:
08/04/2024 to 19/04/2024
-
Context of the visit:
Scientific collaboration with Prof. Vít Dolejší and Petr Tichý and teaching a master course A posteriori error estimates via equilibrated fluxes.
-
Mobility program/type of mobility:
(research stay)
10.2 National initiatives
Participants: Zhaonan Dong, Alexandre Ern, Michel Kern, Géraldine Pichot.
The team is part of the recently created GDR HydroGEMM (“Hydrogène du sous-sol: étude intégrée de la Genèse... à la Modélisation Mathématique”). One of the thematic axes of the GDR is the mathematical analysis and the numerical simulation hydrogen storage in geological reservoirs.
Alexandre Ern is the Director of the CNRS Thematic Network on Earth and Energies since 01/01/2024. The goal of the network is to foster collaborations on mathematical topics applied to Earth and Environment sciences. The main highlight in 2024 was the one-week workshop organized at Nouan-le-Fuzelier in November 2024, involving four introductory courses and a dozen invited lectures (including one by Martin Vohralík ).
Zhaonan Dong , Michel Kern , and Géraldine Pichot were awarded an ANR PRME grant, called STEERS (Space-Time adaptivE mEthods for subsuRface flow Simulations, 2025-2028). The goal is to develop new robust and efficient methods for the simulation of subsurface flow, using a combined Hybrid High-Order / Discontinuous Galerkin (HHO/DG) method on agglomerated meshes, and to speed up the computations using new space-time adaptive algorithms steered by a posteriori error estimates, aiming at guaranteeing solutions to a given user accuracy. The long term objective is to develop robust, accurate and efficient numerical methods, algorithms and an open-source library for the simulations of CO2 storage in deep geological formations.
Martin Vohralík was awarded an ANR-DFG international grant RANPDEs (Robust adaptivity for nonlinear partial differential equations), for 2025–2028, together with Gregor Gantner (University Bonn). The goal is to prove contraction on each step and cost-optimality of adaptive algorithms for model nonlinear problems, necessarily relying on an interplay between analysis of partial differential equations, numerical analysis, and numerical linear algebra,
Martin Vohralík was awarded an FWO grant AdaptPMod (Model adaptivity in the numerical simulation of porous media flows), for 2025–2028, together with Iuliu Sorin Pop (University Hasselt). The goal is to design automatic switching between a hierarchy of models used in numerical simulations of porous media flows (Darcy, Richards, two-phase, compositional, ...).
11 Dissemination
11.1 Promoting scientific activities
11.1.1 Scientific events: organisation
- Alexandre Ern co-organized (with Paul Vigneaux and Nicolas Seguin) a one-week workshop at Nouan-le-Fuzelier (November 2024) in the framework of the CNRS Thematic Network on Earth and Energies.
- Zhaonan Dong , Michel Kern , Géraldine Pichot and Nicolas Pignet organized the workshop “Polytopal Element Methods in Mathematics and Engineering” (POEMS2024). It took place on December 3rd – 6th, 2024 at the Inria Paris center, and gathered close to 100 participants from over 10 countries, from academia and industry.
- Martin Vohralík (with Guillaume Enchéry, IFP Energies Nouvelles) organized the regular 1-day workshop Journée contrat cadre IFP Energies Nouvelles – Inria.
Member of the organizing committees
Alexandre Ern is a member of the Scientific Committee of the European Finite Element Fair. The 2024 Fair was held at University College London (UK) in June 2024.
11.1.2 Journal
Member of the editorial boards
Alexandre Ern is co-Editor-in-Chief of IMA Journal of Numerical Analysis (IMAJNA) since 01/01/2024. Moreover, he continues to serve as Associate Editor for SIAM Journal on Scientific Computing (SISC), ESAIM Mathematical Modeling and Numerical Analysis (M2AN), Journal of Scientific Computing (JOMP), and Computational Methods in Applied Mathematics (CMAM).
Martin Vohralík is a member of the editorial boards of Acta Polytechnica, Applications of Mathematics, and Computational Geosciences.
Reviewer - reviewing activities
Zhaonan Dong , Alexandre Ern , Michel Kern , and Martin Vohralík served as reviewer for various articles in numerical analysis and computational PDEs.
11.1.3 Invited talks
Alexandre Ern was invited to give the 2024 Von Mises Lecture in Berlin in July 2024. He was also invited to give a Keynote Lecture (the only one in Numerical Analysis) at the 9th Pacific Rim Conference in Mathematics held in Darwin in June 2024. Martin Vohralík was an invited speaker of the “Mathematical Models and Numerical Methods for Multiphysics Systems” conference in Pittsburgh in May 2024 and was invited to deliver the SIAM Geosciences Webinar in September 2024.
11.1.4 Leadership within the scientific community
- Michel Kern is a member of the Scientific Board of ORAP, Organisation Associative du Parallélisme.
- Michel Kern serves at the steering committee of GDR HydroGEMM.
- Martin Vohralík serves in the scientific committee of Summer schools CEA–EDF–INRIA.
- Martin Vohralík serves in the scientific board of the IFP Energies Nouvelles – Inria joint strategic partnership laboratory.
11.1.5 Scientific expertise
-
Michel Kern is a reviewer for the Allocation of Computing Time located at the Juelich Supercomputing Centre in Germany.
Michel Kern is an external member of the board of the Ecole Doctorale Galilée at University Sorbonne Paris-Nord.
11.1.6 Research administration
- Géraldine Pichot is the president of the Commission des utilisateurs des moyens informatiques de Paris (CUMI Paris).
- Géraldine Pichot is a member of the Comité de Suivi Doctoral de Paris (CSD).
- Géraldine Pichot is the contact person at Inria Paris for the Agence pour les Mathématiques en Interaction avec l’Entreprise et la Société AMIES.
- Géraldine Pichot set up an Inria stand at the 13ème Forum Entreprises et Mathématiques (FEM2024)
- Géraldine Pichot is a member of the Conseil du Département Mathématiques Appliquées Polytech Lyon.
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Master (M2): Alexandre Ern , Discontinuous Galerkin methods, 20h, M2, Sorbonne University, France.
- Master (M1): Alexandre Ern , Finite Elements, 15h, M1, ENPC, France.
- Master (M2): Alexandre Ern , Hyperbolic equations, 6h, M2, Sorbonne University, France.
- Master (M2): Michel Kern, Models and numerical methods for subsurface flow, 30h, M2, Université Paris Saclay, France.
- Master (M1): Michel Kern, Advanced numerical analysis, 30h, M1, Institut Galilée, Université Paris-Nord, France.
- Master (M1): Martin Vohralík, Advanced finite elements, 21h, M1, ENSTA (Ecole nationale supérieure de techniques avancées), Paris, France.
- Master (M2): Martin Vohralík, A posteriori error estimates via equilibrated fluxes, 36h, M2, Charles University, Prague, Czech Republic.
11.2.2 Supervision
- Ph.D. defended: Houda Mouhcine , Formal Proofs in Applied Mathematics: A Coq Formalization of Simplicial Lagrange Finite Elements, Decembre 9th, 2024, supervised by Sylvie Boldo (Toccata), François Clément, Micaela Mayero (LIPN), 36
- Ph.D. defended: Ari Rappaport, A posteriori error estimates and adaptivity in numerical approximation of PDEs: regularization, linearization, discretization, and floating point precision, March 22, 2024, supervised by François Févotte (TriScale innov) and Martin Vohralík, 37
- Ph.D. in progress: Nicolas Hugot, A posteriori error estimates for the wave equation, started November 2023, supervised by Alexandre Imperiale (CEA List) and Martin Vohralík
- Ph.D. in progress: Abbas Kabalan , Model order reduction for nonparametrized geometrical variability, started October 2022, supervised by Virginie Ehrlacher and Alexandre Ern
- Ph.D. in progress: Clément Maradei , Robust a posteriori error control and adaptivity with inexact solvers, started October 2023, supervised by Zhaonan Dong and Martin Vohralík
- Ph.D. in progress: Romain Mottier , Hybrid nonconforing methods for elasto-acoustic wave propagation and unfitted meshes, started November 2021, defense expected April 2025, supervised by Alexandre Ern and Laurent Guillot (CEA)
- Ph.D. in progress: Baptiste Plaquevent-Jourdain , Robust methods for solving complementarity problems, started January 2022, Sorbonne University and Université de Sherbrooke (Canada), supervised by Jean-Pierre Dussault (Université de Sherbrooke) and Jean Charles Gilbert
- Ph.D. in progress: Zuodong Wang , Finite element methods for hyperbolic and degenerate parabolic problems, started October 2022, supervised by Alexandre Ern and Zhaonan Dong
- Ph.D. in progress: Daniel Zegarra Vasquez , High-performance simulation of single-phase flows in a fractured porous medium, started October 2021, Géraldine Pichot , Michel Kern , and Martin Vohralík .
- Internship: Dorian Nicou , Master “Analyse, Modélisation et Simultion”, Université Paris-Saclay, April–September 2024, supervised by Michel Kern
- Internship: Tall Ouba, Simulation of advective transport in fractured porous media, June–July 2024, supervised by Géraldine Pichot and Michel Kern
11.2.3 Juries
- Alexandre Ern was member of the Ph.D. defense committees for Joyce Ganthous (University of Pau), Loic Balazi (IP Paris), Benoit Cossart (University of Bordeaux) and Robin Roussel (Sorbonne University)
- Martin Vohralík was member of the Ph.D. defense committee for Miranda Boutilier (Université Côte d'Azur)
11.3 Popularization
11.3.1 Participation in Live events
Michel Kern visited Lycée Lucie Aubrac (Courbevoie, 92) as part of the "1 scientifique, 1 classe: Chiche !" program. Michel Kern , Géraldine Pichot , and Martin Vohralík participated at the “accueil des stagiaires de 3ème” at Inria Paris.
12 Scientific production
12.1 Major publications
- 1 articleA posteriori error estimates and stopping criteria for space-time domain decomposition for two-phase flow between different rock types.SMAI Journal of Computational Mathematics5December 2019, 195-227HALDOI
- 2 articleA Coq Formalization of Lebesgue Integration of Nonnegative Functions.Journal of Automated Reasoning662022, 175–213HALDOI
- 3 inproceedingsA Coq formal proof of the Lax–Milgram theorem.6th ACM SIGPLAN Conference on Certified Programs and ProofsParis, FranceJanuary 2017HALDOI
- 4 articleGuaranteed and robust a posteriori bounds for Laplace eigenvalues and eigenvectors: conforming approximations.SIAM Journal on Numerical Analysis555September 2017, 2228-2254HALDOI
-
5
article
-Version discontinuous Galerkin methods on essentially arbitrarily-shaped elements.Mathematics of Computation91333January 2022, 1-35HALDOI - 6 articleA posteriori error estimates for discontinuous Galerkin methods on polygonal and polyhedral meshes.SIAM Journal on Numerical Analysis6152023, 2352--2380HALDOI
- 7 articleA hybrid high-order locking-free method for linear elasticity on general meshes.Comput. Methods Appl. Mech. Engrg.2832015, 1--21URL: http://dx.doi.org/10.1016/j.cma.2014.09.009DOI
- 8 articleExact computation of an error bound for the balanced linear complementarity problem with unique solution.Mathematical Programming1991-22023, 1221-1238HALDOI
-
9
articleEquivalence of local-and global-best approximations, a simple stable local commuting projector, and optimal
approximation estimates in (div).IMA Journal of Numerical Analysis422April 2022, 1023-1049HALDOI - 10 articleFinite element quasi-interpolation and best approximation.ESAIM Math. Model. Numer. Anal.5142017, 1367--1385URL: https://doi.org/10.1051/m2an/2016066
- 11 articleHybrid high-order methods for flow simulations in extremely large discrete fracture networks.SMAI Journal of Computational Mathematics82022, 375-398HALDOI
- 12 articlePolynomial-degree-robust a posteriori estimates in a unified setting for conforming, nonconforming, discontinuous Galerkin, and mixed discretizations.SIAM Journal on Numerical Analysis532April 2015, 1058-1081HALDOI
- 13 articleA generalized mixed hybrid mortar method for solving flow in stochastic discrete fracture networks.SIAM J. Sci. Comput.3412012, B86--B105URL: http://dx.doi.org/10.1137/100804383DOI
12.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Doctoral dissertations and habilitation theses
Reports & preprints
Software
12.3 Cited publications
- 67 techreportA Levenberg-Marquardt globalization of the polyhedral Newton-min algorithm for complementarity problems.oui2023back to text
- 68 techreportPrimal and dual approaches for the chamber enumeration of real hyperplane arrangements.back to text
- 69 inproceedingsScalable Domain Decomposition Preconditioners for Heterogeneous Elliptic Problems.Proceedings of the International Conference on High Performance Computing, Networking, Storage and AnalysisSC '13New York, NY, USADenver, ColoradoAssociation for Computing Machinery2013DOIback to text
- 70 articleKSPHPDDM and PCHPDDM: Extending PETSc with advanced Krylov methods and robust multilevel overlapping Schwarz preconditioners.Computers & Mathematics with Applications842021, 277-295DOIback to text

