Section: New Results

Stochastic modeling for complex and biological systems

Participants: R. Azaïs, T. Bastogne, C. Lacaux, A. Muller-Gueudin, S. Tindel, P. Vallois, S. Wantz-Mézières

Modelisation of networks of multiagent systems

We relate here the beginning of collaboration between A. Gueudin, R. Azaïs and some automatic control researchers in Nancy.

We consider networks, modeled as a graph with nodes and edges representing the agents and their interconnections, respectively. The connectivity of the network, persistence of links and interactions reciprocity influence the convergence speed towards a consensus.

The problem of consensus or synchronization is motivated by different applications as communication networks, power and transport grids, decentralized computing networks, and social or biological networks.

We then consider networks of interconnected dynamical systems, called agents, that are partitioned into several clusters. Most of the agents can only update their state in a continuous way using only inner-cluster agent states. On top of this, few agents also have the peculiarity to rarely update their states in a discrete way by resetting it using states from agents outside their clusters. In social networks, the opinion of each individual evolves by taking into account the opinions of the members belonging to its community. Nevertheless, one or several individuals can change its opinion by interacting with individuals outside its community. These inter-cluster interactions can be seen as resets of the opinions. This leads us to a network dynamics that is expressed in term of reset systems. We suppose that the reset instants arrive stochastically following a Poisson renewal process.

Tumor growth modeling

A cancer tumor can be represented for simplicity as an aggregate of cancer cells, each cell behaving according to the same discrete model and independently of the others. Therefore to measure its size evolution, it seems natural to use tools coming from dynamics of population, for instance the logistic model. This deterministic framework is well-known but the stochastic one is worthy of interest. We are currently studying in [22] a model in which we suppose that the size $V_t$ at time $t$ of the tumor is a diffusion process of the type :

where ${\left(B_t\right)}_{t\ge 0}$ is a standard brownian motion starting from zero.Then (i) We define a family of time continuous Markov chains which models the evolution of the rate of malignant cells and approximate (under some conditions) the diffusion process $\left(V_t\right)$. (ii) We study in depth the solution to equation (3 ). This diffusion process lives in a domain delimited by two boundaries: 0 and $\kappa >0$. In this stochastic setting, the role of $\kappa$ is not so clear and we contribute to understand it. We describe the asymptotic behavior of the diffusion according to the values of the parameters. The tools we resort to are boundary classification criteria and Laplace transform of the hitting time to biological worthwhile level. We are able in particular to express the mean of the hitting time.

Anisotropic random fields

Hermine Biermé (Tours) and Céline Lacaux follow in [19] their collaboration in the study of anisotropic random fields. They have extended their previous works in the framework of conditionally sub-Gaussian random series. For such anisotropic fields, they have obtained a modulus of continuity and a rate of uniform convergence. Their framework allows to study e.g., Gaussian fields, stable random fields and multi-stable random fields.

Inference for dynamical systems driven by Gaussian noises.

As mentioned in the Scientific Foundations Section, the problem of estimating the coefficients of a general differential equation driven by a Gaussian process is still largely unsolved. To be more specific, the most general ($ℝ$-valued) equation handled up to now as far as parameter estimation is concerned is of the form:

where $\theta$ is the unknown parameter, $b$ is a smooth enough coefficient and $B$ is a one-dimensional fractional Brownian motion. In contrast with this simple situation, our applications of interest (see the Application Domains Section) require the analysis of the following ${ℝ}^n$-valued equation:

where $\theta$ enters non linearly in the coefficient, where $\sigma$ is a non-trivial diffusion term and $B$ is a $d$-dimensional fractional Brownian motion. We have thus decided to tackle this important scientific challenge first.

To this aim, here are the steps we have focused on in 2014:

• A better understanding of the underlying rough path structure for equation (4 ). This includes two studies on differential systems driven by some general Gaussian noises in infinite dimensions: [17] on the Parabolic Anderson model, and [16] about viscosity solutions in the rough paths setting.

• Study of densities for general systems driven by Gaussian noises as in [18] and [15] .

• Ergodic aspects, which are another important ingredient for estimation procedures for stochastic differential equations, are handled in [3] .

Extremal process

In extreme value theory, one of the major topics is the study of the limiting behavior of the partial maxima of a stationary sequence. When this sequence is i.i.d., the unique limiting process is well-known and called the extremal process. Considering a long memory stable sequence, the limiting process is obtained as a simple power time change extremal process. Céline Lacaux and Gennady Samorodnistky have proved in [23] that this limiting process can also be interpreted as a restriction of a self-affine random sup measure. In addition, they have established that this random measure arises as a limit of the partial maxima of the same long memory stable sequence, but in a different space. Their results open the way to propose new self-similar processes with stationary max-increments.

Self-nested structure of plants

In a recent work, Godin and Ferraro designed a method to compress tree structures and to quantify their degree of self-nestedness. This method is based on the detection of isomorphic subtrees in a given tree and on the construction of a DAG, equivalent to the original tree, where a given subtree class is represented only once (compression is based on the suppression of structural redundancies in the original tree). In the compressed graph, every node representing a particular subtree in the original tree has exactly the same height as its corresponding node in the original tree.

The degree of self-nestedness is defined as the edit-distance between the considered tree structure and its nearest embedded self-nested version. Indeed, finding the nearest self-nested tree of a structure without more assumptions is conjectured to be an NP-complete or NP-hard problem. We thus design a heuristic method based on interacting simulated annealing algorithms to tackle this difficult question. This procedure is also a keystone in a new topological clustering algorithm for trees that we propose in this work. In addition, we obtain new theoretical results on the combinatorics of self-nested structures. For instance, we have shown that the number $C_{\le H}\left(m\right)$ of self-nested trees with maximal height $H$ and a ramification number for each vertex less than $m$ satisfies the following formula,

In particular, the cardinality $C_{=h}\left(m\right)$ of self-nested trees with exact height $h$ evolves according to

when $m$ and $h$ simultaneously go to infinity. The redaction of an article is currently in progress.

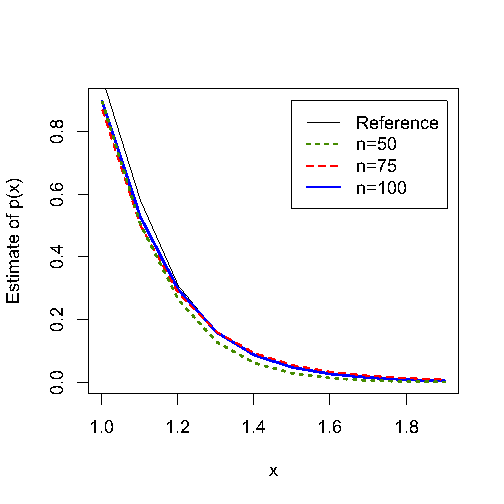
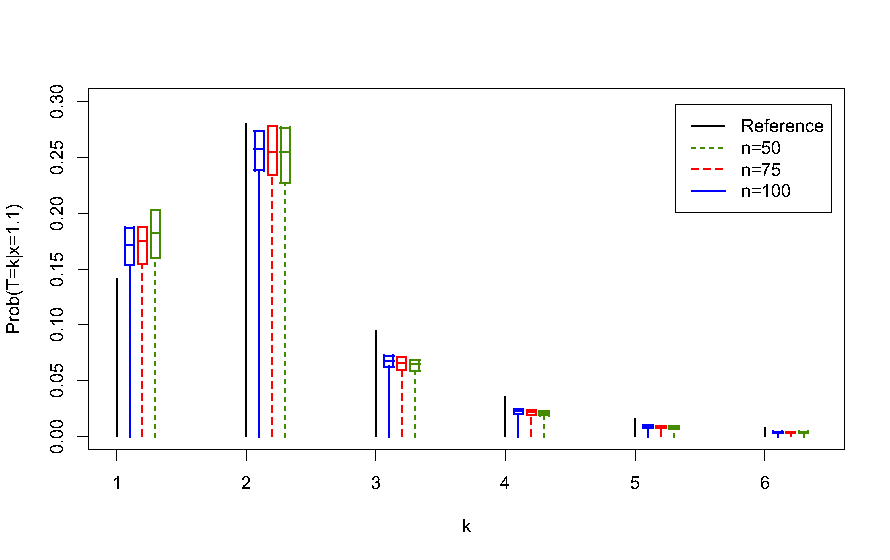
Semi-parametric inference for a growth-fragmentation model

Statistical inference for piecewise-deterministic Markov processes has been extensively investigated for a few years under some ergodicity conditions. Our paper [2] is dedicated to a statistical approach for a particular non ergodic growth-fragmentation model for which the set $[0,1]$ is absorbing. This kind of stochastic process may model the dynamic of a malthusian population for which there exists an extinction threshold. We focus on the estimation of the extinction probability and of the distribution of the extinction time from only one path of the model within a long time interval.

We establish that the absorption probability $p$ is the unique solution in an appropriate space of a Fredholm equation of the second kind whose parameters are unknown,

where $K$ is an integral operator depending explicitly on the main features of the model. From $n$ data, we estimate this important characteristic of the underlying process by solving numerically the estimated Fredholm equation. Indeed, ${\widehat{p}}_{n,m}$ is defined as the approximated solution of the equation $p-{\widehat{K}}_{n}p={\widehat{s}}_n$ after $m$ steps of the algorithm. Fortunately, this procedure allows us to estimate also the extinction time.

We have shown the convergence in probability of the proposed estimators under some usual asymptotic conditions. In particular, we have,

when $n$ and $m$ simultaneously go to infinity. The good behavior of our estimates on finite sample sizes is presented in Figure 6 . In future works, we plan to apply this methodology to more intricate situations, in particular for the pharmacokinetics and pharmacodynamics stochastic models recently introduced in the literature.

A Model-based Pharmacokinetics Characterization Method of Engineered Nanoparticles for Pilot Studies

Recent developments on engineered multifunctional nanomaterials have opened new perspectives in oncology. But assessment of both quality and safety in nanomedicine requires new methods for their biological characterization. We have recently proposed a new model-based approach for the pre-characterization of multifunctional nanomaterials pharmacokinetics in small scale in vivo studies. Two multifunctional nanoparticles, with and without active targeting, designed for photodynamic therapy guided by magnetic resonance imaging are used to exemplify the presented method. It allows the experimenter to rapidly test and select the most relevant pharmacokinetic (PK in the sequel) model structure planned to be used in the subsequent explanatory studies. We also show that the model parameters estimated from the in vivo responses provide relevant preliminary information about the tumor uptake, the elimination rate and the residual storage. For some parameters, the accuracy of the estimates is good enough to compare and draw significant pre-conclusions. A third advantage of this approach is the possibility to optimally refine the in vivo protocol for the subsequent explanatory and confirmatory studies complying with the 3Rs (reduction, refinement, replacement) ethical recommendations. More precisely, we show that the identified model may be used to select the appropriate duration of the magnetic resonance imaging sessions planned for the subsequent studies. The proposed methodology integrates magnetic resonance image processing, continuous-time system identification algorithms and statistical analysis. Except, the choice of the model parameters to be compared and interpreted, most of the processing procedure may be automated to speed up the PK characterization process at an early stage of experimentation.

More specifically, our efforts have been split into the following tasks:

• The article [6] gives an application of statistical methods for the design of experiments to optimize the formulation of a composite molecule in photodynamic therapy. The associated know-how has been transferred to the start-up CYBERnano to be generalized to the rational design of engineered nanoparticles. Collaboration with CRAN and LRGP (Nancy) and UNINE (Neuchâtel, Suisse).

• In [12] , in vivo application of photodynamic therapy, a mathematical model and computational simulations of the light propagation in biological tissues were developed to help biologists to determine a priori some parameters of the experimental protocol. More precisely, the numerical results were used to select the most suited position of the optical fiber to be implemented within the animal brain. This equipment is required to bring the light and thus activate the molecule within the tumor. The therapeutical objective was to maximize the homogeneity of light intensity within the tumor volume.

• Obstacles and challenges to the clinical use of the photodynamic therapy (PDT) are numerous: large inter-individual variability, heterogeneity of therapeutic predictability, lack of in vivo monitoring concerning the reactive oxygen species (ROS) production, etc. All of these factors affect in their ways the therapeutic response of the treatment and can lead to a wild uncertainty on its efficiency. To deal with these variability sources, we have designed and developed an innovative technology able to adapt in realtime the width of light impulses during the photodynamic therapy. The first objective is to accurately control the photobleaching trajectory of the photosensitizer during the treatment with a subsequent goal to improve the efficacy and reproducibility of this therapy. In this approach, the physician a priori defines the expected trajectory to be tracked by the photosensitizer photobleaching during the treatment. The photobleaching state of the PS is regularly measured during the treatment session and is used to change in real-time the illumination signal. This adaptive scheme of the photodynamic therapy has been implemented, tested and validated during in vitro tests. These tests show that controlling the photobleaching trajectory is possible, confirming the technical feasibility of such an approach to deal with inter-individual variabilities in PDT. These results, contained in [13] , open new perspectives since the illumination signal can be different from a patient to another according to his individual response. This study has proven its interest by showing promising results in an in vitro context, which has to be confirmed by the current in vivo experiments. However, it is fair to say that in a near future, the proposed solution could lead, in fine, to an optimized and personalized PDT. A patent was deposited subsequently. Collaboration with CRAN (Nancy).

• The communications [8] , [9] and [10] present successful applications of a model-based design of nanoparticles. This approach is based on statistical design of experiments and black-box modeling in cell biology. The associated know-how has been transferred to the start-up CYBERnano. Collaboration with CEA LETI and INSERM (Grenoble).