Section: New Results

Dealing with uncertainties

Sensitivity Analysis for Forecasting Ocean Models

Participants : Eric Blayo, Laurent Gilquin, Céline Helbert, François-Xavier Le Dimet, Elise Arnaud, Simon Nanty, Maëlle Nodet, Clémentine Prieur, Laurence Viry, Federico Zertuche.

Scientific context

Forecasting geophysical systems require complex models, which sometimes need to be coupled, and which make use of data assimilation. The objective of this project is, for a given output of such a system, to identify the most influential parameters, and to evaluate the effect of uncertainty in input parameters on model output. Existing stochastic tools are not well suited for high dimension problems (in particular time-dependent problems), while deterministic tools are fully applicable but only provide limited information. So the challenge is to gather expertise on one hand on numerical approximation and control of Partial Differential Equations, and on the other hand on stochastic methods for sensitivity analysis, in order to develop and design innovative stochastic solutions to study high dimension models and to propose new hybrid approaches combining the stochastic and deterministic methods.

Estimating sensitivity indices

A first task is to develop tools for estimated sensitivity indices. In variance-based sensitivity analysis, a classical tool is the method of Sobol' [68] which allows to compute Sobol' indices using Monte Carlo integration. One of the main drawbacks of this approach is that the estimation of Sobol' indices requires the use of several samples. For example, in a $d$-dimensional space, the estimation of all the first-order Sobol' indices requires $d+1$ samples. Some interesting combinatorial results have been introduced to weaken this defect, in particular by Saltelli [66] and more recently by Owen [64] but the quantities they estimate still require $O\left(d\right)$ samples.

In a recent work [71] we introduce a new approach to estimate all first-order Sobol' indices by using only two samples based on replicated latin hypercubes and all second-order Sobol' indices by using only two samples based on replicated randomized orthogonal arrays. We establish theoretical properties of such a method for the first-order Sobol' indices and discuss the generalization to higher-order indices. As an illustration, we propose to apply this new approach to a marine ecosystem model of the Ligurian sea (northwestern Mediterranean) in order to study the relative importance of its several parameters. The calibration process of this kind of chemical simulators is well-known to be quite intricate, and a rigorous and robust — i.e. valid without strong regularity assumptions — sensitivity analysis, as the method of Sobol' provides, could be of great help. The computations are performed by using CIGRI, the middleware used on the grid of the Grenoble University High Performance Computing (HPC) center. We are also applying these estimates to calibrate integrated land use transport models. As for these models, some groups of inputs are correlated, Laurent Gilquin extended the approach based on replicated designs for the estimation of grouped Sobol' indices [6] .

We can now wonder what are the asymptotic properties of these new estimators, or also of more classical ones. In [54] , the authors deal with asymptotic properties of the estimators. In [52] , the authors establish also a multivariate central limit theorem and non asymptotic properties.

Sensitivity analysis with dependent inputs

An important challenge for stochastic sensitivity analysis is to develop methodologies which work for dependent inputs. For the moment, there does not exist conclusive results in that direction. Our aim is to define an analogue of Hoeffding decomposition [53] in the case where input parameters are correlated. Clémentine Prieur supervised Gaëlle Chastaing's PhD thesis on the topic (defended in September 2013) [44] . We obtained first results [45] , deriving a general functional ANOVA for dependent inputs, allowing defining new variance based sensitivity indices for correlated inputs. We then adapted various algorithms for the estimation of these new indices. These algorithms make the assumption that among the potential interactions, only few are significant. Two papers have been recently accepted [43] , [46] . We also considered (see the paragraph 7.3.1 ) the estimation of groups Sobol' indices, with a procedure based on replicated designs. These indices provide information at the level of groups, and not at a finer level, but their interpretation is still rigorous.

Céline Helbert and Clémentine Prieur supervised the PhD thesis of Simon Nanty (funded by CEA Cadarache, and defended in October, 2015). The subject of the thesis is the analysis of uncertainties for numerical codes with temporal and spatio-temporal input variables, with application to safety and impact calculation studies. This study implied functional dependent inputs. A first step was the modeling of these inputs, and a paper has been submitted [63] . The whole methodology proposed during the PhD is under advanced revision [36] .

Multy-fidelity modeling for risk analysis

Federico Zertuche's PhD concerns the modeling and prediction of a digital output from a computer code when multiple levels of fidelity of the code are available. A low-fidelity output can be obtained, for example on a coarse mesh. It is cheaper, but also much less accurate than a high-fidelity output obtained on a fine mesh. In this context, we propose new approaches to relieve some restrictive assumptions of existing methods ( [57] , [65] ): a new estimation method of the classical cokriging model when designs are not nested and a nonparametric modeling of the relationship between low-fidelity and high-fidelity levels. The PhD takes place in the REDICE consortium and in close link with industry. The first part of the thesis was also dedicated to the development of a case study in fluid mechanics with CEA in the context of the study of a nuclear reactor.

The second part of the thesis was dedicated to the development of a new sequential approach based on a course to fine wavelets algorithm. Federico Zertuche presented his work at the annual meeting of the GDR Mascot Num in 2014 [72] .

Data assimilation and second order sensitivity analysis

Basically, in the deterministic approach, a sensitivity analysis is the evaluation of a functional depending on the state of the system and of parameters. Therefore it is natural to introduce an adjoint model. In the framework of variational data assimilation the link between all the ingredients (observations, parameters and other inputs of the model is done through the optimality system (O.S.), therefore a sensitivity will be estimated by deriving the O.S. leading to a second order adjoint. This is done in the paper [15] in which a full second order analysis is carried out on a model of the Black Sea.

This methodology has been applied to

• Oil Spill. These last years have known several disasters produced by wrecking of ships and drifting platforms with severe consequences on the physical and biological environments. In order to minimize the impact of these oil spills its necessary to predict the evolution of oil spot. Some basic models are available and some satellites provide images on the evolution of oil spots. Clearly this topic is a combination of the two previous one: data assimilation for pollution and assimilation of images. A theoretical framework has been developed with Dr. Tran Thu Ha (iMech).

• Data Assimilation in Supercavitation (with iMech). Some self propelled submarine devices can reach a high speed thanks to phenomenon of supercavitation: an air bubble is created on the nose of the device and reduces drag forces. Some models of supercavitation already exist but are working on two applications of variational methods to supercavitation:

  • Parameter identification : the models have some parameters that can not be directly measured. From observations we retrieve the unknown parameters using a classical formalism of inverse problems.

  • Shape Optimization. The question is to determine an optimum design of the shape of the engine in order to reach a maximum speed.

Optimal Control of Boundary Conditions

Participants : Christine Kazantsev, Eugene Kazantsev.

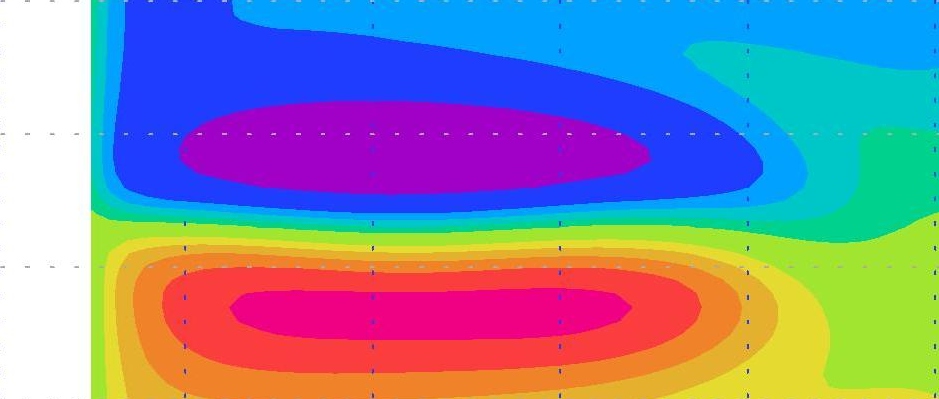
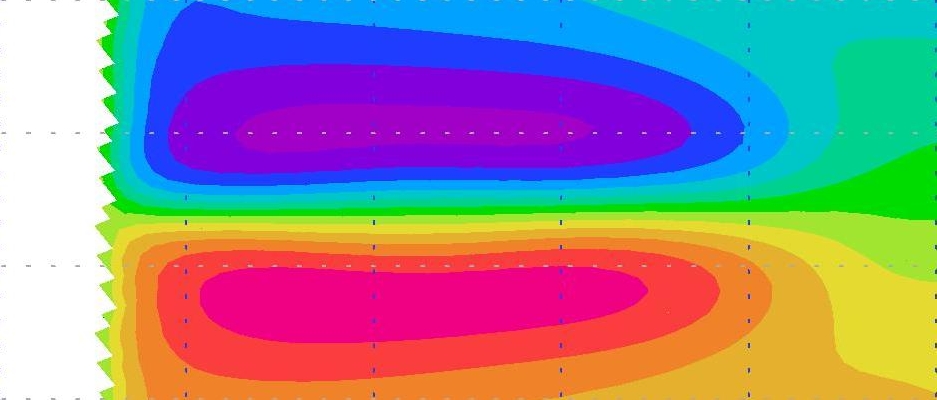
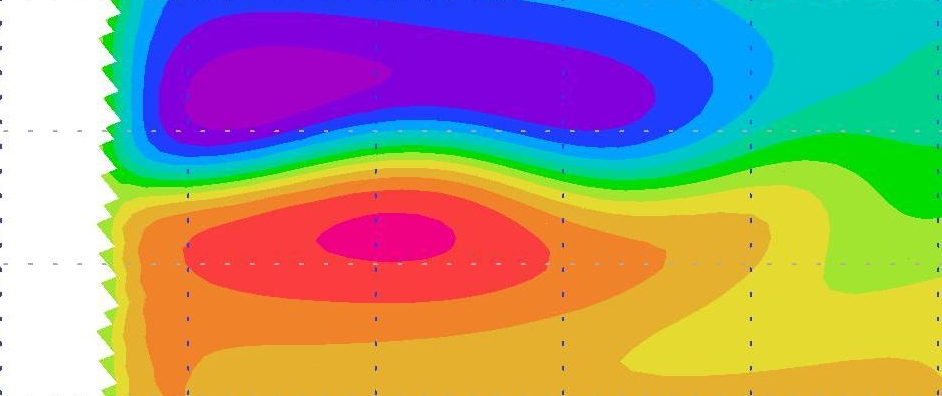
A variational data assimilation technique is applied to the identification of the optimal boundary conditions for a simplified configuration of the NEMO model. A rectangular box model placed in mid-latitudes, and subject to the classical single or double gyre wind forcing, is studied. The model grid can be rotated on a desired angle around the center of the rectangle in order to simulate the boundary approximated by a staircase-like coastlines. The solution of the model on the grid aligned with the box borders was used as a reference solution and as artificial observational data. It is shown in [9] , [10] that optimal boundary has a rather complicated geometry which is neither a staircase, nor a straight line. The boundary conditions found in the data assimilation procedure bring the solution toward the reference solution allowing to correct the influence of the rotated grid (see fig. 1 ).

Adjoint models, necessary to variational data assimilation, have been produced by the TAPENADE software, developed by the SCIPORT team. This software is shown to be able to produce the adjoint code that can be used in data assimilation after a memory usage optimization.

Non-Parametric Estimation for Kinetic Diffusions

Participants : Clémentine Prieur, Jose Raphael Leon Ramos.

This research is the subject of a collaboration with Venezuela and is partly funded by an ECOS Nord project.

We are focusing our attention on models derived from the linear Fokker-Planck equation. From a probabilistic viewpoint, these models have received particular attention in recent years, since they are a basic example for hypercoercivity. In fact, even though completely degenerated, these models are hypoelliptic and still verify some properties of coercivity, in a broad sense of the word. Such models often appear in the fields of mechanics, finance and even biology. For such models we believe it appropriate to build statistical non-parametric estimation tools. Initial results have been obtained for the estimation of invariant density, in conditions guaranteeing its existence and unicity [40] and when only partial observational data are available. A paper on the non parametric estimation of the drift has been accepted recently [41] (see Samson et al., 2012, for results for parametric models). As far as the estimation of the diffusion term is concerned, a paper has been accepted [41] , in collaboration with J.R. Leon (Caracas, Venezuela) and P. Cattiaux (Toulouse). Recursive estimators have been also proposed by the same authors in [42] , also recently accepted.20

Note that Professor Jose R. Leon (Caracas, Venezuela) is now funded by an international Inria Chair and will spend one year in our team, allowing to collaborate further on parameter estimation.

Multivariate Risk Indicators

Participants : Clémentine Prieur, Patricia Tencaliec.

Studying risks in a spatio-temporal context is a very broad field of research and one that lies at the heart of current concerns at a number of levels (hydrological risk, nuclear risk, financial risk etc.). Stochastic tools for risk analysis must be able to provide a means of determining both the intensity and probability of occurrence of damaging events such as e.g. extreme floods, earthquakes or avalanches. It is important to be able to develop effective methodologies to prevent natural hazards, including e.g. the construction of barrages.

Different risk measures have been proposed in the one-dimensional framework . The most classical ones are the return level (equivalent to the Value at Risk in finance), or the mean excess function (equivalent to the Conditional Tail Expectation CTE). However, most of the time there are multiple risk factors, whose dependence structure has to be taken into account when designing suitable risk estimators. Relatively recent regulation (such as Basel II for banks or Solvency II for insurance) has been a strong driver for the development of realistic spatio-temporal dependence models, as well as for the development of multivariate risk measurements that effectively account for these dependencies.

We refer to [47] for a review of recent extensions of the notion of return level to the multivariate framework. In the context of environmental risk, [67] proposed a generalization of the concept of return period in dimension greater than or equal to two. Michele et al. proposed in a recent study [48] to take into account the duration and not only the intensity of an event for designing what they call the dynamic return period. However, few studies address the issues of statistical inference in the multivariate context. In [49] , [51] , we proposed non parametric estimators of a multivariate extension of the CTE. As might be expected, the properties of these estimators deteriorate when considering extreme risk levels. In collaboration with Elena Di Bernardino (CNAM, Paris), Clémentine Prieur is working on the extrapolation of the above results to extreme risk levels.

Elena Di Bernardino, Véronique Maume-Deschamps (Univ. Lyon 1) and Clémentine Prieur also derived an estimator for bivariate tail [50] . The study of tail behavior is of great importance to assess risk.

With Anne-Catherine Favre (LTHE, Grenoble), Clémentine Prieur supervises the PhD thesis of Patricia Tencaliec. We are working on risk assessment, concerning flood data for the Durance drainage basin (France). The PhD thesis started in October 2013. A first paper on data reconstruction has been accepted [18] . It was a necessary step as the initial series contained many missing data.