Section: Highlights of the Year
Highlights of the Year
Freestart collision for the full SHA-1.
Together with M. Stevens and T. Peyrin, P. Karpman gave the first freestart collision for the full SHA-1 hash function [32] . Although theoretical attacks on this function were known since 2005, this work is an important milestone in SHA-1 cryptanalysis and it had a concrete impact on the use of SHA-1 in existing systems, such as TLS certificates. In particular, the CA/Browser forum (which regroups some of the major industries of the internet) withdrew an internal ballot proposing to extend the use of SHA-1 in new certificates through 2016. Major browser developers such as Mozilla are also encouraging the timely withdrawal of SHA-1 certificates by updating the in-browser security warnings when such certificates are used. This result was also vulgarised in technical press such as Ars Technica and more general newspapers such as Le monde.
Discrete logarithm record computation in finite fields
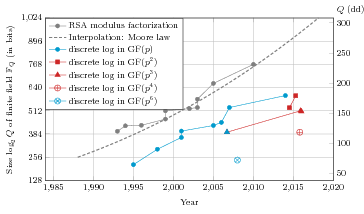
F. Morain and A. Guillevic together with P. Gaudry (CARAMEL team, Inria Nancy Grand Est) and R. Barbulescu (CNRS, IMJ) published a new discrete logarithm record in a finite field of 180 decimal digits (dd), i.e. 595 bits. This result was presented at the Eurocrypt 2015 conference [19] . The Discrete Logarithm Problem (DLP) is widely studied in prime fields GF and was broken in small characteristic finite fields of the form GF and GF with smooth very recently. It was not known whether the DLP is as hard in extensions of finite fields compared to prime fields, for the same global size. With this record of the same size as the most recent record in a prime field, F. Morain and A. Guillevic showed that DLP in GF is much faster than in a prime field of the same size, and even faster than a factorization of an RSA modulus of the same size.
| Algorithm | relation collection | linear algebra | total |
| NFS-IF | 5 years | 5.5 months | 5.5 years |
| NFS-DL | 50 years | 80 years | 130 years |
| NFS-DL | 157 days | 18 days (GPU) | 0.5 years |
F. Morain and A. Guillevic contributed with P. Gaudry and E. Thomé to other DL computation records in finite fields GF of 508 bits and 512 bits, and GF of 392 bits. The practical difficulty is increasing with the extension degree.
|
CATREL conference
The 1st and 2nd of October 2015, F. Morain, B. Smith and A. Guillevic organized an international workshop to conclude the CATREL project. There were 14 invited speakers from all around the world, from Palaiseau with A. Guillevic to as far as Auckland in New Zealand with S. Galbraith. A. Joux presented an historical summary of DL computation from the 80's. P. Gaudry, E. Thomé and C. Bouvier from the Caramel Team (Inria Nancy), presented their contribution, and K. Bhargavan presented the Logjam attack. There were also members of abroad teams leader in discrete logarithm record breaking. G. Adj from Mexico and R. Granger and T. Kleinjung presented their recent records in small characteristic.
We hosted more than 50 participants for the two intensive days of the workshop. The schedule of the workshop is available on the following link. http://www.lix.polytechnique.fr/cryptologie/CATREL-workshop
AGCT 15
A. Couvreur was one of the organizers of the conference AGCT 15 (Arithmetic Geometry Cryptography and Coding Theory) at CIRM (Marseille).