Section: New Results

Entanglement between stationary and propagating modes

Participants: B. Huard and F. Mallet.

The results of this section were published in [14] .

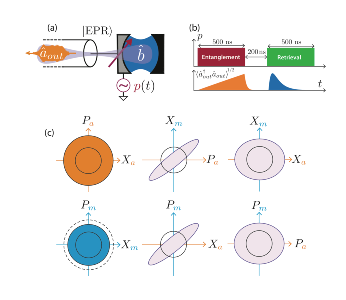
Entanglement being instrumental in quantum machines, we have shown how a Josephson mixer can generate and distribute entangled microwave radiations on separated transmission lines and different frequencies by spontaneous parametric down-conversion in 2012. Using two Josephson mixers, we have provided the first demonstration of entanglement between spatially separated propagating fields in the microwave domain. Therefore, a new variety of entangled states, the so-called EPR states (after Einstein, Podolsky and Rosen), which are encoded on continuous variables, is now available in this frequency range.

In 2015, we have shown that it could constitute the central component of a potential quantum network based on continuous-variable entanglement. The device essentially acts as a regular mixer performing frequency conversion but without adding extra noise. Used as a switch, it is able to open and close the coupling to a high-quality factor cavity in a time-controlled way. We have demonstrated how this feature leads to a new kind of quantum memory. Coupled to its ability to generate entanglement, we have demonstrated the time-controlled generation, storage and on-demand release of an entangled state, which is the prerequisite for the node of a quantum network.

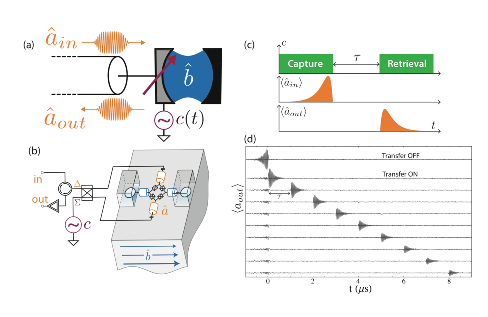
Several implementations of quantum memories for microwave radiation have been realized in the past few years. In order to store the state of microwave signals, some use spin ensembles  [81] , [130] , [71] , or mechanical oscillators  [98] , while others use superconducting cavities with tunable input coupling  [124] , [102] . Our own implementation is sketched in Fig. 3 b, where the Josephson Mixer allows an on-demand access to the long lived 3D cavity based on noiseless frequency conversion. Its main advantage consists in the ability to generate entanglement between the memory and the output port.

Noiseless frequency conversion is another regime of the Josephson mixer. The frequency of the pump tone is now chosen to be at the difference between the frequencies of the modes $\widehat{a}$ and $\widehat{b}$, $\Omega =|{\omega }_a-{\omega }_b|$. In the rotating frame, the effective Hamiltonian reduces to a beam-splitter Hamiltonian with an implicit frequency conversion:

The elementary process corresponds to the conversion of photons between the mode a and b mediated by the pump at a rate $\chi |\langle \widehat{c}\rangle |$ as sketched in Fig. 3 c. Therefore, the noiseless frequency conversion generates a coupling between the long lived cavity mode $\widehat{b}$ and the propagating modes at the input of mode $\widehat{a}$. This pump field can then be varied in time to switch on and off the coupling.

A first measurement consists in the capture, storage and retrieval of a microwave pulse. The protocol is quite simple, we turn the pump tone on when the incoming pulse reaches the memory input. The signal pulse has been designed such that it is optimally absorbed by the memory. The pump tone is turned off after the absorption and turned back on at a later time $\tau$ to retrieve the pulse in the transmission line. The measured output amplitude in time shown in Fig. 3 d demonstrate that this protocol can be performed with a great efficiency for a few microseconds.

However, the unique ability of this device lies in the possibility to combine this storage operation with the entanglement generation demonstrated previously. A second measurement consists in the generation, storage and characterization of an EPR state distributed between the memory and the transmission line. The protocol is sketched in Fig. 4 b. The pump is first applied at $\Omega ={\omega }_a+{\omega }_b$ to generate an EPR state shared between the memory and the propagating mode. The propagating mode complex amplitude is measured and at a later time, the pump is turned on again at $\Omega =|{\omega }_a-{\omega }_b|$ to activate the noiseless conversion. The memory mode is then retrieved in the transmission line and its complex amplitude is measured. By analyzing the cross-correlations between these two measurements, we have been able to show that the memory preserves the entanglement of the EPR state. Furthermore, the contours of the EPR state Wigner function have been inferred from this correlation measurement (Fig. 4 c) and the entanglement quantified.