Section: Research Program
The scientific context
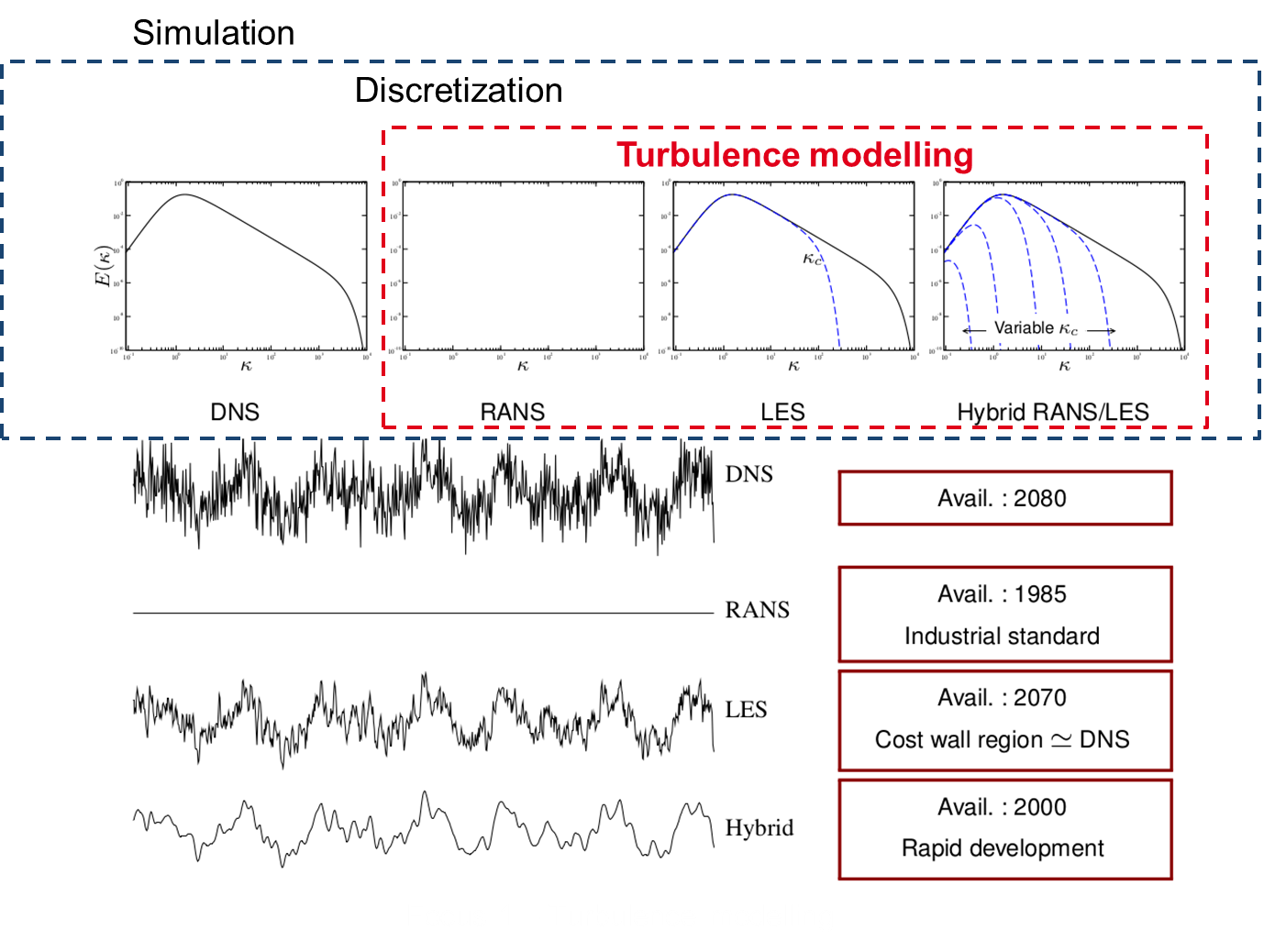
Computational fluid mechanics: modeling or not before discretizing ?
A typical continuous solution of the Navier-Stokes equations at sufficiently large values of the Reynolds number is governed
by a wide spectrum of temporal and spatial scales closely connected with the turbulent nature of the flow. The term deterministic chaos employed by Frisch in his enlightening book [46] is certainly conveying most adequately the difficulty in analyzing and simulating this kind of flows.
The broadness of the turbulence spectrum is directly controlled by the Reynolds number defined as the ratio between the inertial forces and the viscous forces. This number is not only useful to determine the transition from a laminar to a turbulent flow regime, it also indicates the range of scales of fluctuations that are present in the flow under consideration. Typically, for the velocity field and far from solid walls, the ratio between the largest scale (the integral length scale) and the smallest one (Kolmogorov scale) is proportional to
To the noticeable exception of the hybrid RANS-LES modeling, which is not yet accepted as a reliable tool for industrial design, as mentioned in the preamble of the Go4hybrid European program (https://cordis.europa.eu/project/rcn/109107/factsheet/en), a turbulence model represents turbulent mechanisms in the same way in the whole flow. Thus, depending on its intrinsic strengths and weaknesses, accuracy will be a rather volatile quantity, strongly dependent on the flow configuration. For instance, RANS is perfectly suited to attached boundary layers, but exhibits severe limitations in massively-separated flow regions. Therefore, the turbulence modeling and industrial design communities waver between the desire to continue to rely on the RANS approach, which is unrivaled in terms of computational cost, but is still not able to accurately represent all the complex phenomena; and the temptation to switch to LES, which outperforms RANS in many situations, but is prohibitively expensive in high-Reynolds number wall-bounded flows. In order to account for the limitations of the two approaches and to combine them for significantly improving the overall performance of the models, the hybrid RANS-LES approach has emerged during the last two decades as a viable, intermediate way, and we are definitely inscribing our project in this innovative field of research, with an original approach though, based on temporal filtering (Hybrid temporal LES, HTLES) rather than spatial filtering, and a systematic and progressive validation process against experimental data produced by the team.
|
Computational fluid mechanics: high order discretization on unstructured meshes and efficient methods of solution
All the methods considered in the project are mesh-based methods: the computational domain is divided into cells, that have an elementary shape:
triangles and quadrangles in two dimensions, and tetrahedra, hexahedra, pyramids, and prisms in three dimensions. If the cells are only regular hexahedra, the mesh is said to be structured. Otherwise, it is said to be unstructured. If the mesh is composed of more than one sort of elementary shape, the mesh is said to be hybrid. In the project, the numerical strategy is based on discontinuous Galerkin methods. These methods were introduced by Reed and Hill [57] and first studied by Lesaint and Raviart [53]. The extension to the Euler system with explicit time integration was mainly led by Shu, Cockburn and their collaborators. The steps of time integration and slope limiting were similar to high-order ENO schemes,
whereas specific constraints given by the finite-element nature of the scheme were gradually solved for scalar conservation laws [41], [40],
one dimensional systems [39], multidimensional scalar conservation laws [38], and multidimensional systems [42]. For the same system, we can
also cite the work of [45], [50], which is slightly different: the stabilization is made by adding a nonlinear term, and the time
integration is implicit. In contrast to continuous Galerkin methods, the discretization of diffusive operators is not straightforward. This is due to the discontinuous
approximation space, which does not fit well with the space function in which the diffusive system is well posed. A first stabilization was proposed by Arnold [31]. The first application of discontinuous Galerkin methods to Navier-Stokes equations was proposed in [36] by
mean of a mixed formulation. Actually, this first attempt led to a non-compact computational stencil, and was later proved to be unstable.
A compactness improvement was made in [37], which was later analyzed, and proved to be stable in a more
unified framework [32]. The combination with the
-
The computational stencil of one given cell is limited to the cells with which it has a common face. This stencil does not depend on the order of approximation. This is a pro, compared for example with high-order finite volumes, for which the number of neighbors required increases with the order of approximation.
-
They can be developed for any kind of mesh, structured, unstructured, but also for aggregated grids [34]. This is a pro compared not only with finite-difference schemes, which can be developed only on structured meshes, but also compared with continuous finite-element methods, for which the definition of the approximation basis is not clear on aggregated elements.
-
-
Upwinding is as natural as for finite volumes methods, which is a benefit for hyperbolic problems.
-
As the formulation is weak, boundary conditions are naturally weakly formulated. This is a benefit compared with strong formulations, for example point centered formulation when a point is at the intersection of two kinds of boundary conditions.
For concluding this section, there already exists numerical schemes based on the discontinuous Galerkin method, which proved to be efficient for computing compressible viscous flows. Nevertheless, there remain many things to be improved, which include: efficient shock capturing methods for supersonic flows, high-order discretization of curved boundaries, low-Mach-number behavior of these schemes and combination with second-moment RANS closures. Another aspect that deserves attention is the computational cost of discontinuous Galerkin methods, due to the accurate representation of the solution, calling for a particular care of implementation for being efficient. We believe that this cost can be balanced by the strong memory locality of the method, which is an asset for porting on emerging many-core architectures.
Experimental fluid mechanics: a relevant tool for physical modeling and simulation development
With the considerable and constant development of computer performance, many people were thinking at the turn of the 21st century that in the short term, CFD would replace experiments, considered as too costly and not flexible enough. Simply flipping through scientific journals such as Journal of Fluid Mechanics, Combustion and Flame, Physics of Fluids or Journal of Computational Physics or through websites such that of Ercoftac (http://www.ercoftac.org) is sufficient to convince oneself that the recourse to experiments to provide either a quantitative description of complex phenomena or reference values for the assessment of the predictive capabilities of models and simulations is still necessary. The major change that can be noted though concerns the content of the interaction between experiments and CFD (understood in the broad sense). Indeed, LES or DNS assessment calls for the experimental determination of temporal and spatial turbulent scales, as well as time-resolved measurements and determination of single or multi-point statistical properties of the velocity field. Thus, the team methodology incorporates from the very beginning an experimental component that is operated in strong interaction with the modeling and simulation activities.