Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
- A6.3.4. Model reduction
- A6.5.1. Solid mechanics
- A6.5.2. Fluid mechanics
- A9.2. Machine learning
Other Research Topics and Application Domains
- B2.2.1. Cardiovascular and respiratory diseases
- B4.2. Nuclear Energy Production
- B4.3.2. Hydro-energy
- B4.3.3. Wind energy
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B5.5. Materials
1 Team members, visitors, external collaborators
Research Scientists
- Michel Bergmann [INRIA, Researcher, HDR]
- Tommaso Taddei [INRIA, Researcher]
Faculty Members
- Angelo Iollo [Team leader, UNIV BORDEAUX, Professor, HDR]
- Afaf Bouharguane [UNIV BORDEAUX, Associate Professor]
Post-Doctoral Fellows
- Umberto Bosi [Inria, from Apr 2022]
- Antoine Fondaneche [UNIV BORDEAUX]
- Birgul Koc [IFPEN, from Jun 2022]
- Nishant Kumar [Inria]
PhD Students
- Eki Agouzal [EDF]
- Beatrice Battisti [ECOLE POLYT. TURIN]
- Maxime Chapron [ONERA, from Oct 2022]
- Jon Labatut [ONERA, from Oct 2022]
- Caroline Anna-Lise Andrea Le Guern [IFPEN]
- Karl Maroun [UNIV POITIERS]
- Thomas Philibert [ECOLE POLYT. TURIN]
- Michele Romanelli [ONERA]
- Ludovica Saccaro [INRIA]
- Giulia Sambataro [ANDRA]
- Alexis Tardieu [UNIV BORDEAUX]
Technical Staff
- Philippe Depouilly [CNRS, Engineer, from Feb 2022]
Administrative Assistant
- Anne-Laure Gautier [INRIA]
External Collaborator
- Majdi Azaiez [BORDEAUX INP, HDR]
2 Overall objectives
2.1 Multi-physics numerical modeling
2.1.1 Reduced-order models: convergence between PDE models and data
Unprecedented opportunities exist to directly use already collected computational or experimental data to improve and build predictive models that can be used online for the simulation of parametric problems, robust design, and control in science and engineering. In this regard, our goal is to combine mechanistic causal models based on partial differential equations (PDEs) with large data sets to reduce the marginal cost of predictions.
Reduced-order models (ROMs) are our main tool for this purpose. ROMs are parametric mathematical models derived from the full set of PDEs using previously computed solutions. In many applications, the solution space turns out to be low-dimensional, so one can trade a minimal loss of accuracy for speed and scalability. ROMs counteract the curse of dimensionality by significantly reducing computational complexity.
Overall, ROMs have reached a certain level of maturity during the last decade, allowing their implementation in large-scale industrial codes, mainly in structural mechanics. Nevertheless, some hard points stand. Parametric problems governed by strong advection fields or sensibly compact-support solutions such as moving shocks suffer from a limited possibility of dimensional reduction and, at the same time, insufficient generalization of the model (out-of-sample solutions). The main reason for this is that the solution space is usually approximated by an affine or linear representation, which is intrinsically broad band for such problems.
We have worked on the development of model order reduction (MOR) techniques for nonlinear, advection-dominated problems, with emphasis on projection-based Galerkin and Petrov-Galerkin ROMs. First, we worked on the development of effective sampling strategies to reduce training costs. Second, we developed nonlinear, registration-based approximation techniques, to overcome limitations of linear approximation methods (e.g., proper orthogonal decomposition, POD) to deal with strong advection fields. Third, we developed hybrid formulations that combine reduced-order and full-order models to deal with complex flow features and/or complex parameterizations.
2.1.2 Schemes for Hierarchical meshes, multi-physics and asymptotic limits
The schemes we have developed aim at simulating complex multiphysics phenomena through appropriate PDE modeling, automatic implicit geometry representation (level sets), hierarchical Cartesian schemes (quad-octrees), parallel simulations, and accurate treatment of boundaries. Discretization schemes on hierarchical meshes allow multiscale solution of PDEs on non-body-fitted meshes with a drastic reduction in computational setup overhead. The key idea is to use an octree mesh to approximate the solution fields, while the geometry is captured by level set functions. The boundary conditions are determined by appropriate interpolation methods to achieve sufficient accuracy. This approach eliminates the need for boundary conforming meshes, which require time-consuming and error-prone mesh generation procedures, and opens the door to easy parallel simulation of very complex geometries.
One of the limitations of this approach is that a mesh with a fixed aspect ratio is not optimal for very anisotropic fields such as boundary layers. For such cases, we explored the idea of using a body-fitted grid near the immersed obstacles and a hierarchical mesh in the background. Essentially, we use the techniques we have developed to impose boundary conditions on non-body-matched meshes further from the boundary, where the solution is smoother and more isotropic. Our current investigations build on discontinuous Galerkin (DG) methods / ADER approaches to combine efficient interpolation strategies at the grid interfaces and compact reconstruction of the data at the grid level.
Part of our activity has been dedicated to improve schemes for all Mach number flows in both fluid dynamics and continuum mechanics. Phenomena of interest involve fluid flows and elastic materials whose deformations are investigated within a monolithic Eulerian framework. With this approach any material (gas, liquid or solid) can be described with the same system of conservation equations and a suitable general formulation of the constitutive law.
These schemes are accurate in computing steady state solutions as well as in approximating material wave propagation in various Mach regimes and different materials. We are presently studying methods to overcome the need to solve for auxiliary relaxation variables while preserving the properties of the linearly implicit schemes. To achieve this, we split the stiff relaxation source terms from the fluxes and then reformulate the homogeneous part in an elliptic form.
3 Research program
Coherently with our investigation approach, we start from real-world applications to identify key methodological problems, then, we study those problems and develop new methods to address them; finally, we implement these methods for representative test cases to demonstrate their practical relevance.
3.1 Numerical models
We aim to further develop automated model-order reduction (MOR) procedures for large-scale systems in computational mechanics — here, automated refers to the ability to complete the analysis with minimal user intervention. First, we wish to combine nonlinear MOR with mesh adaptation to simultaneously learn rapid and reliable ROMs and effective high-fidelity discretizations over a range of parameters. Second, we wish to develop component-based MOR procedures to build inter-operable components for steady and unsteady nonlinear PDEs: towards this end, we should develop efficient localized training procedures to build local ROMs for each archetype component, and also domain decomposition techniques to glue together the local models for prediction. We also wish to develop and analyze hybrid approaches that combine and merge first-principle models with data-fit models, and also full-order and reduced-order models for prediction of global engineering quantities of interest.
We envision that several methods that are currently developed in the team can be complemented by available tools from machine learning: representative examples include — but are not limited to — solution clustering, optimal sampling, classification. In this respect, a leap forward in industrial applications that we will pursue is without doubts the possibility of capitalizing on previous experience drawn from already acquired simulations to build non-intrusive models that combine non-linear interpolations and non-linear regression. New perspectives in this direction are offered by the Chair Onera-Nouvelle Aquitaine (cf. Highlights).
As regards the work on numerical discretization of PDEs, compared to the previous evaluation, we focus on the representation of the solution in each computational cell by adopting a DG/ADER approach to improve the resolution of solution's discontinuities. This approach is complemented with a Chimera grid at the boundaries in order to improve accuracy by a body fitted mesh avoiding grid generation complexity for a general, possibly varying, geometrical topology. The thesis of Alexis Tardieu, which started in October 2021 and is funded by the University of Bordeaux, studies this approach. Still in this direction, we will continue to study asymptotic schemes for multi-materials applications: our aim is to devise a unified approach to handle both compressible and incompressible materials.
In parallel, we will continue our exploration of schemes that circumvent the problem of accuracy and time stepping in the asymptotic regimes such as low- and high Mach numbers for multi-material flows: the ultimate goal is to devise asymptotic-preserving schemes that are able to capture phenomena at the time scale of the fast waves and of the material waves with the same accuracy, exclusively choosing the appropriate time-scale.
3.2 Applications
For energy applications, we will continue our investigations on wave energy converters and windturbines. Relative to wave energy converters, we are developing multifidelty models that couple the incompressible Navier-Stoke equations (NSE) around the floater with a Proper Orthogonal (POD) ROM or a simplified-physics model elsewhere.
- In October 2021, Nishant Kumar started a two-year postdoctoral fellowship in the team, which was funded by the Inria-IfpEN program; the aim is to couple an high-fidelity model and a POD model based on the LES Navier-Stokes equations; the coupling is implemented in the SOWFA framework of OpenFOAM.
- In December 2021, Caroline Le Guern started her PhD in the team, in the framework of the Inria-IfpEN program; Caroline works on the modeling and simulation of the fluid-structure interaction of next-generation windturbines with up to 250 meter rotor; the numerical implementation is based on the software Deeplines that is co-developed by IfpEN.
- In April 2022, Umberto Bosi started a two-year postdoctoral fellowship in the team, in collaboration with CARDAMOM: the project of Umberto, which was funded by Inria and the Region Nouvelle Aquitaine, focuses on the coupling between an high-fidelity (e.g., Navier-Stokes) model and an asymptotic (e.g., shallow water or Boussinesq) model.
We are also collaborating with EDF to devise effective ROMs for parametric studies. In this collaboration, we emphasize the implementation of projection-based ROMs for real-world applications exploiting industrial codes.
- In April 2021, Eki Agouzal started an industrial thesis to develop projection-based ROMs for nonlinear structural mechanics problems in Code Aster, with emphasis on thermo-hydro-mechanical (THM) applications.
- A PhD thesis is expected to start in October 2023 on the development of MOR techniques for the shallow water equations in the EDF code Telemac-Mascaret.
Within the ARIA project, in collaboration with Nurea and the bio-mechanics lab of the Politecnico di Torino, we investigate the idea of data augmentation starting from a given aneurysm database. We will construct statistically relevant synthetic aneurysms that can provide both heterogeneity and closeness to reality to test new bio-markers for aneurysm rupture. The thesis of Ludovica Saccaro funded by Inria is dedicated to this subject.
In the framework of the ANR DRAGON, we also increase our interactions with researchers in biology and physical science. in the center of biological studies in Chizé (centre d'études biologiques de Chizé). The ANR funds the PhD thesis of Karl Maroun at University of Poitiers.
The software development will be continued. We will pursue the development of the NEOS library: NEOS will be distributed in open source LGPL-3.0. The HIWIND software will be rewritten based on NEOS library.
4 Application domains
4.1 Energy conversion
We apply the methods developed in our team to the domain of wind engineering and sea-wave converters. In Figure 1, we show results of a numerical model for a sea-wave energy converter. We here rely on a monolithic model to describe the interaction between the rigid floater, air and water; material properties such as densities, viscosities and rigidity vary across the domain. The appropriate boundary conditions are imposed at interfaces that arbitrarily cross the grid using adapted schemes built thanks to geometrical information computed via level set functions 46. The background method for fluid-structure interface is the volume penalization method 38 where the level set functions is used to improve the degree of accuracy of the method 4 and also to follow the object. The underlined mathematical model is unsteady, and three dimensional; numerical simulations based on a grid with degrees of freedom are executed in parallel using 512 CPUs.

See-wave converter


In the context of the Aerogust (Aeroelastic gust modelling) European project, together with Valorem, we investigated the behavior of wind turbine blades under gust loading. The aim of the project was to optimize the design of wind turbine blades to maximize the power extracted. A meteorological mast (Figure 2(a)) has been installed in March 2017 in Brittany to measure wind on-site: data provided by the mast have been exploited to initialize the mathematical model. Due to the large cost of the full-order mathematical model, we relied on a simplified model 44 to optimize the global twist. Then, we validated the optimal configuration using the full-order Cartesian model based on the NaSCar solver. Figure 2(b) shows the flow around the optimized optimized wind turbine rotor.
4.2 Schemes for turbulent flow simulations using Octrees
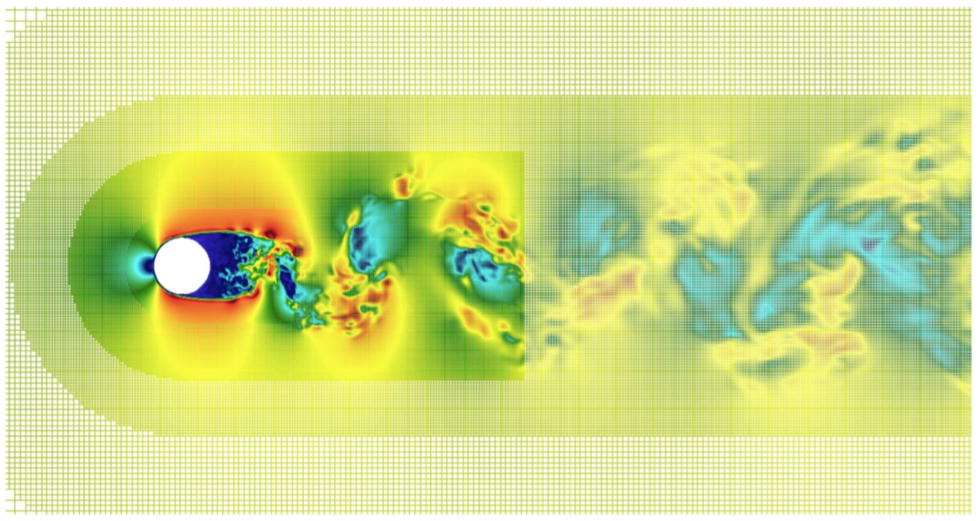
We have initially developed and tested a 3D first-order Octree code for unsteady incompressible Navier-Stokes equations for full windmill simulations with an LES model and wall laws. We have validated this code on Occigen for complex flows at increasing Reynolds numbers. This step implied identifying stable and feasible schemes compatible with the parallel linear Octree structure. The validation has been conducted with respect to the results of a fully Cartesian code (NaSCAR) that we run on Turing (with significantly more degrees of freedom) and with respect to experimental results.
Subsequently, we have developed a second-order Octree scheme that has been validated on Occigen for a sphere at a moderate Reynolds number (), see Table 1. Then, for a cylinder at () (Figures 3(a) and 3(b)), close to real applications, we have preliminary validation results for the second-order scheme with respect to experimental drag coefficient (Table 2). Additional resources will be asked on Occigen to complete the study.
| Mesh | number of cells | (1st-order scheme) | (2nd-order scheme) | |
| 1 | N.A. | |||
| 2 | ||||
| 3 | ||||
| 4 |
| Case | |
| Octree, 1st-order scheme | |
| Octree, 2nd-order scheme | |
| Cartesian | |
| Experimental estimate 41 |

4.3 Vascular flows
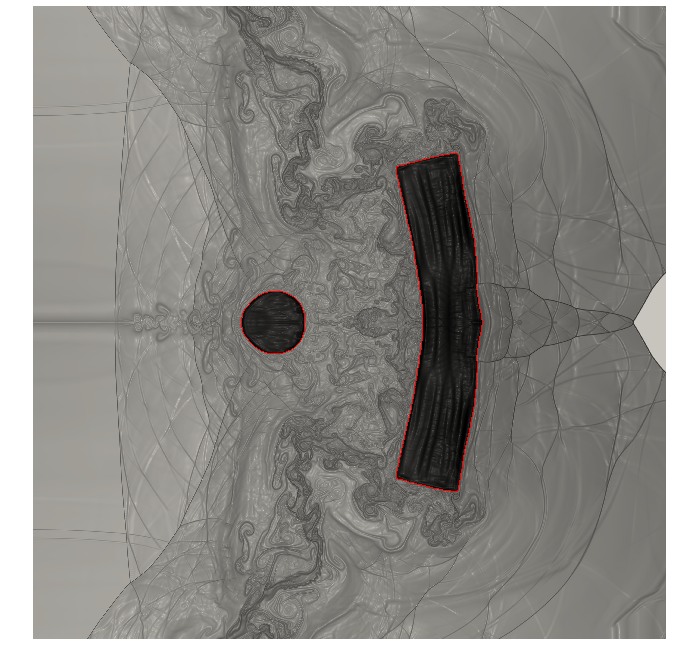
A new research direction pursued by the team is the mathematical modelling of vascular blood flows in arteries. Together with the start-up Nurea and the surgeon Eric Ducasse, we aim at developing reliable and automatic procedures for aneurysm segmentation and for the prediction of aneurysm rupture risk. Our approach exploits two sources of information: (i) numerical simulations of blood flows in complex geometries, based on an octree discretization, and (ii) computed tomography angiography (CTA) data. Figure 4 shows the force distribution on the walls of the abdominal aorta in presence of an aneurysm; results are obtained using a parallelized hierarchical Cartesian scheme based on octrees.
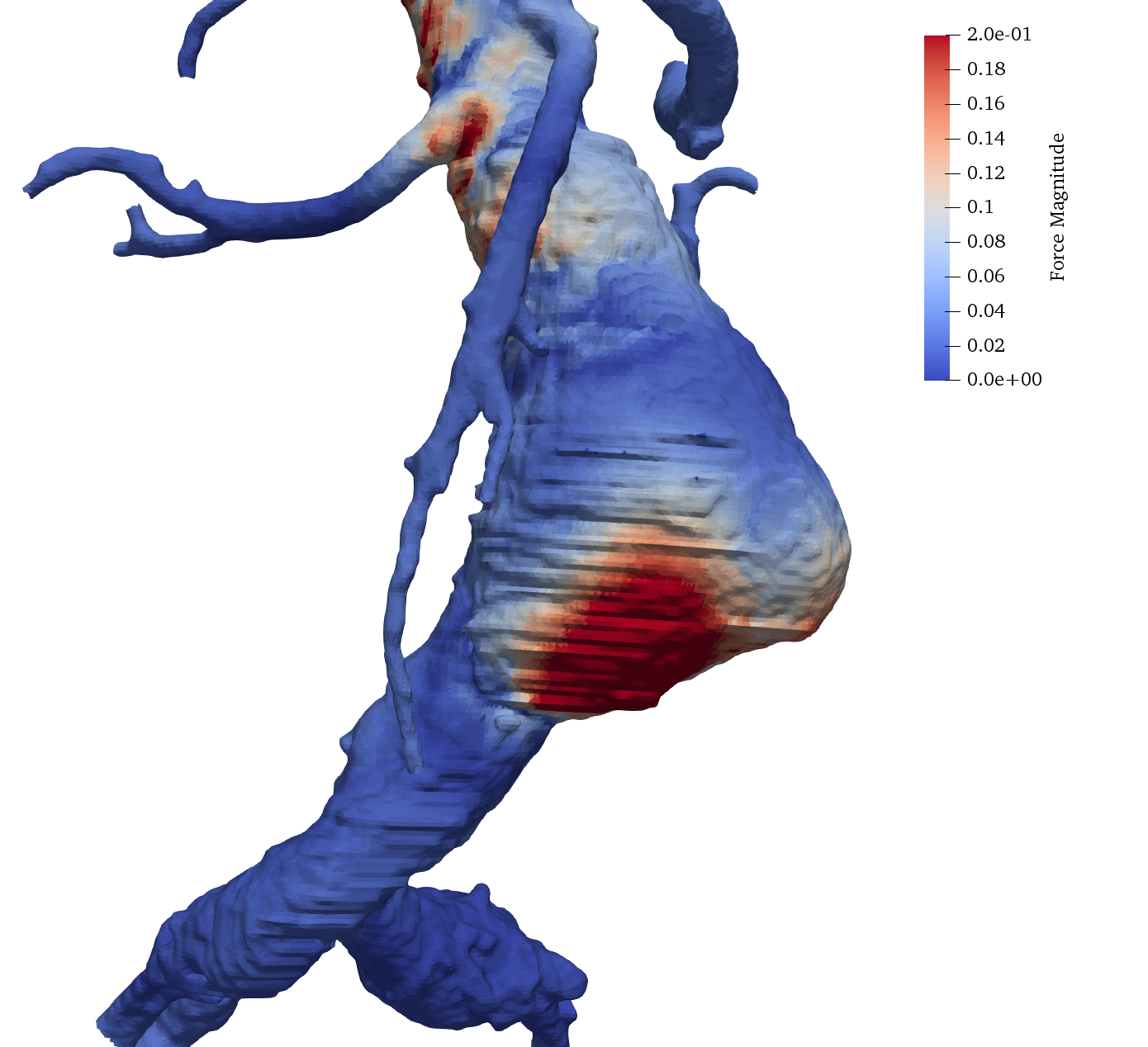
Aneurysm simulation
4.4 Fluid-structure interactions using Eulerian non-linear elasticity models
Mathematical and numerical modeling of continuum systems undergoing extreme regimes is challenging due to the presence of large deformations and displacements of the solid part, and due to the strongly non-linear behavior of the fluid part. At the same time, proper experiments of impact phenomena are particularly dangerous and require expensive facilities, which make them largely impractical. For this reason, there is a growing interest in the development of predictive models for impact phenomena.
In MEMPHIS, we rely on a fully Eulerian approach based on conservation laws, where the different materials are characterized by their specific constitutive laws, to address these tasks. This approach was introduced in 43 and subsequently pursued and extended in 45, 42, 39, 40 and 9. In Figure 5, we show the results of the numerical simulation of the impact of a copper projectile immersed in air over a copper shield. Results are obtained using a fully parallel monolithic Cartesian method, based on a fixed Cartesian grid. Simulations are performed on a cluster of 512 processors, and benefits from the isomorphism between grid partitioning and processor topology.

In figure 6, we show the results of a three dimensional simulation of a cardiac pump (LVAD, left ventricule assisted device).
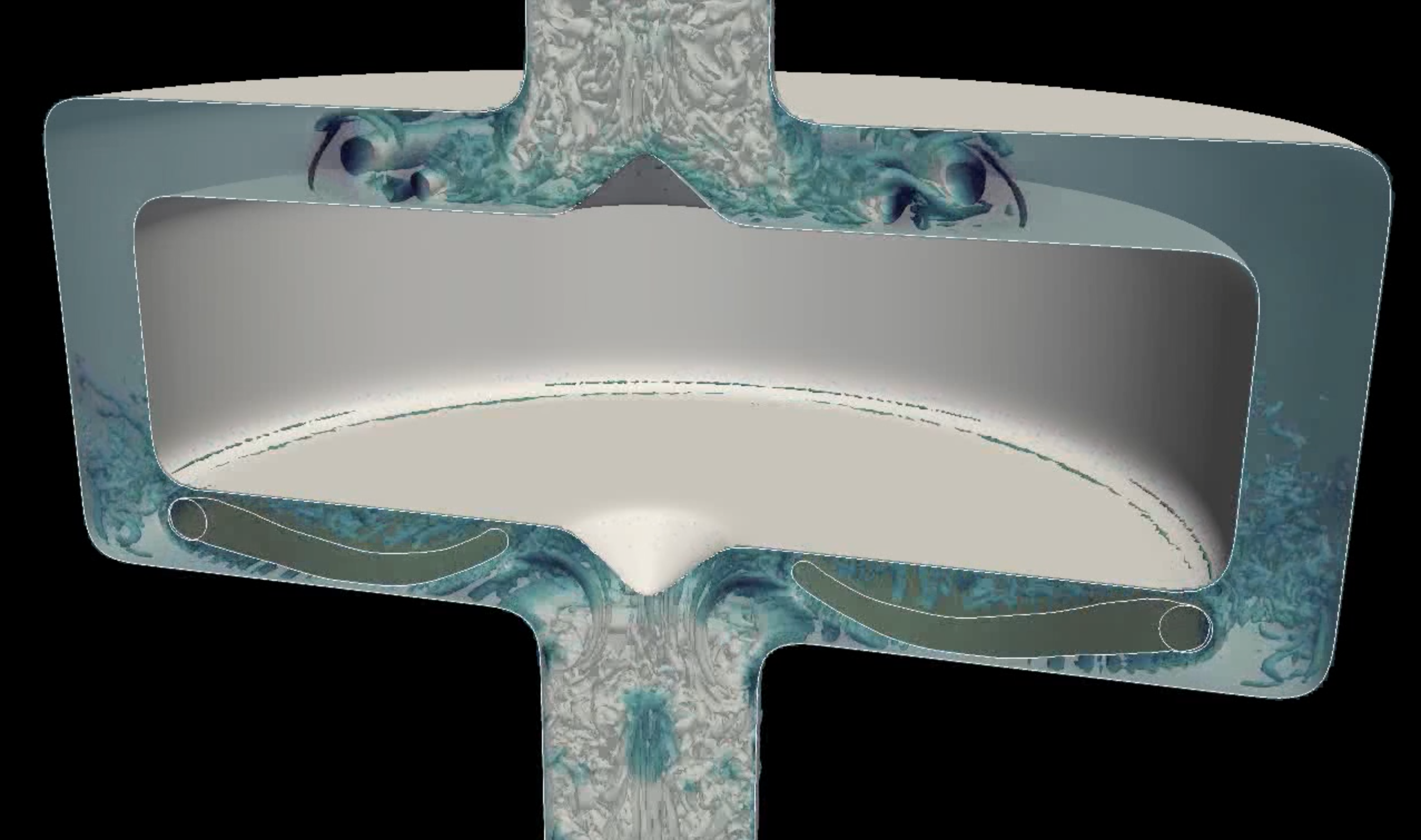
Cardiac pump simulation
Other examples are given in the sections dedicated to the new results.
5 Social and environmental responsibility
As discussed in the previous section, we are particularly interested in the development of mathematical models and numerical methods to study problems related to renewable energies, and ultimately contribute to next-generation sustainable solutions for energy extraction.
5.1 Impact of research results
We are studying two types of green energy extractors: wave energy converters (WECs) and wind energy.
As regards WECs, we are working with the PoliTO (Torino, Italy) to model the behavior of inertial sea wave energy converters (ISWEC), and we are also starting to work with a Bordeaux-based start-up for another device to extract energy from waves via an Inria-Tech project and a Nouvelle-Aquitaine Regional Project submitted by Memphis in collaboration with the CARDAMOM team.
As regards wind energy, we focus on the analysis of wind turbines. In the past, we have supervised two PhD CIFRE theses with VALOREM-Valeol, and are currently working with them in a European RISE ARIA project led by Memphis. We also work with IFPEN on the aeroelastic modeling of large wind turbines and the study and optimization of turbines farms in the framework of the joint laboratory Inria-IFPEN with a thesis funded by IFPEN and a post-doc funded by Inria (which started in October 2021).
In conjunction with these activities, in collaboration with ANDRA (the national agency for storage of nuclear waste), we investigate the development of reduced-order models to allow efficient and accurate simulations for deep geological storage planning. This activity is the subject of the PhD thesis of Giulia Sambataro.
6 Highlights of the year
In November 2022, the region Nouvelle-Aquitaine approved the funding of the partnership (Chaire) PROVE (Propulsion pour l’energie vert) between ONERA (the French aeronautics, space and defense research laboratory) and several academic institutions in the French region Nouvelle Aquitaine; the project is led by Dr. Denis Sipp at Onera and Prof. Angelo Iollo at Inria Bordeaux.The Chair PROVE aims to develop mathematical methods that combine physical models and data to design, optimize and control complex aeronautical systems.
The Chaire PROVE funds 6 PhD theses and 2 two-year postdoctoral fellowships in team MEMPHIS in the time period 2021-2024. Three PhD theses have started in 2021 and 2022; the remaining three PhD theses and two postdocs will be funded in 2024.
- The PhD thesis of Michele Romanelli, which started in October 2021, focuses on the development of wall models for high-Reynolds flows.
- The PhD thesis of Maxime Chapron, which started in October 2022, aims to devise effective dimensionality reduction strategies based on the active subspace method, for the design and optimization of aerodynamic systems.
- The PhD thesis of Jon Labatut, which started in October 2022, focuses on the development of nonlinear approximation methods for aerodynamic flows with parameter-dependent discontinuities.
7 New results
7.1 Component-based model order reduction for radioactive waste management
Participants: Angelo Iollo, Giulia Sambataro, Tommaso Taddei.
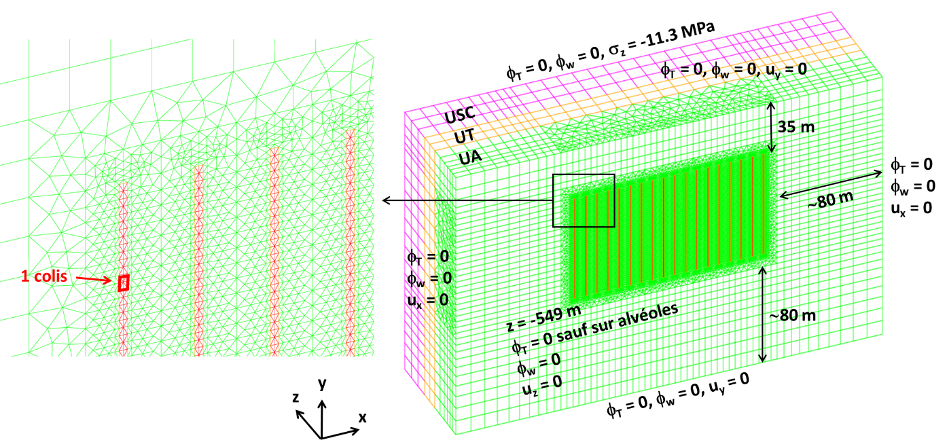
At the end of their cycle, radioactive materials are placed in arrays of cylindrical boreholes (dubbed alveoli) deep underground; due to the large temperatures of the radioactive waste, the thermal flux generated by the alveoli drives a complex time-dependent phenomenon which involves the thermal, hydraulic and mechanical (THM) response of the medium. The role of simulations is to predict the long-term system response and ultimately assess the impact of the repository site to the surrounding areas: Figure 7(a) shows a typical system configuration considered for numerical investigations.
Due to the complex nature of the equations (a system of five coupled nonlinear time-dependent three-dimensional equations) and due to the uncertainty in several parameters of the model and on boundary conditions, MOR techniques are important to reduce the computational burden associated with thorough parametric studies. In particular, it is important to study the system behavior for different numbers of alveoli: it is possible to show that changing the number of alveoli induces a change in the topology of the problem and thus prevents the application of standard monolithic MOR techniques developed for fixed domains or diffeomorphic families of parametric domains. We should thus devise component-based MOR procedures that are compatible with topology changes.
The PhD project of Giulia Sambataro aimed to devise a rapid and reliable component-based MOR technique for THM systems, for radioactive waste management applications. During the first year of her PhD, Giulia developed a monolithic MOR technique for THM systems which relies on a POD-Greedy algorithm to sample the parameter domain and to hyper-reduction based on empirical quadrature to reduce online prediction costs. During the second and third year, Giulia developed a component-based MOR formulation — which is dubbed one-shot overlapping Schwartz (OS2) method — for nonlinear steady PDEs and finally she extended the approach to THM systems with varying numbers of alveoli.
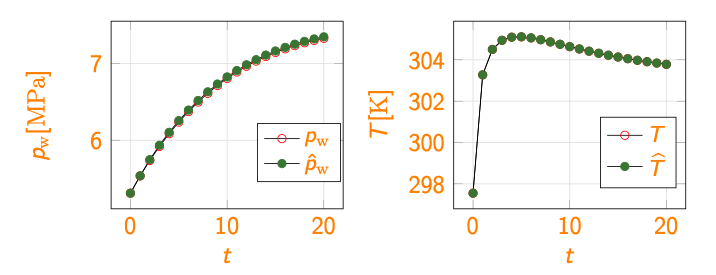
Giulia successfully defended her PhD thesis in December 2022; her work led to the publication of two articles on peer-reviewed journals, 20 and 33. Figure 7(b) shows the temporal behavior of the HF and predicted pressure and temperature in a select point in the proximity of one alveolus for an out-of-sample configuration. We observe that the ROM is able to adequately predict the solution behavior; in our numerical experiments, we experienced an average 20x speed-up over the range of configurations.
7.2 Registration methods for advection-dominated PDEs
Participants: Angelo Iollo, Tommaso Taddei.
A major issue of state-of-the-art MOR techniques based on linear approximation spaces is the inability to deal with parameter-dependent sharp gradients, which characterize the solutions to advection-dominated problems. To address this issue, we propose a registration technique to align local features in a fixed reference domain. In computer vision and pattern recognition, registration refers to the process of finding a transformation that aligns two datasets; here, registration refers to the process of finding a parametric spatio-temporal transformation that improves the linear compressibility of the solution manifold.
A registration procedure has been proposed in 47 and then further developed in 49, 48, 18. In particular, in 49, we considered the application to one-dimensional applications in hydraulics; in an ongoing collaboration with EDF, we aim to extend the approach to two-dimensional steady and unsteady problems. Figure 8 shows results for a Saint-Venant problem (flow past a bump): Figures 8(a) and 8(b) show the free surface for two different parameters and two time instants, while Figure 8(c) shows the behavior of the out-of-sample projection error associated with a snapshot-based POD space with and without registration. We observe that registration is key to improve performance of linear compression strategies such as POD.
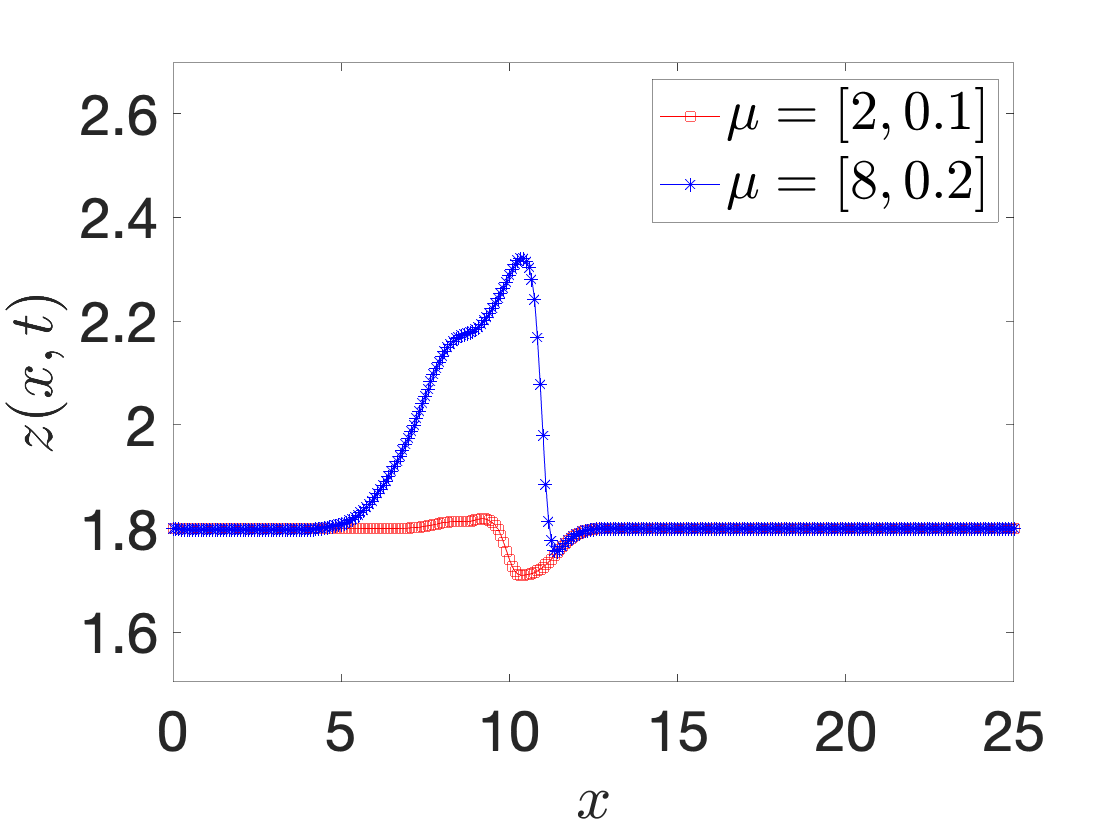
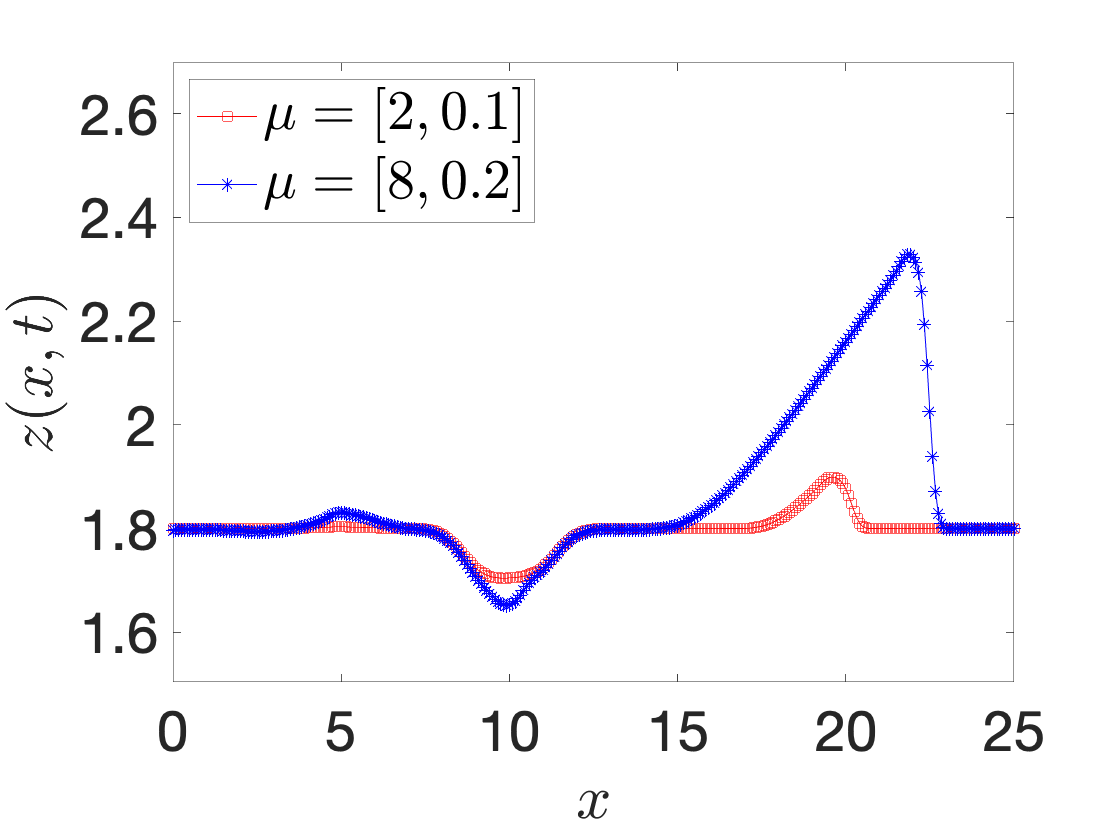
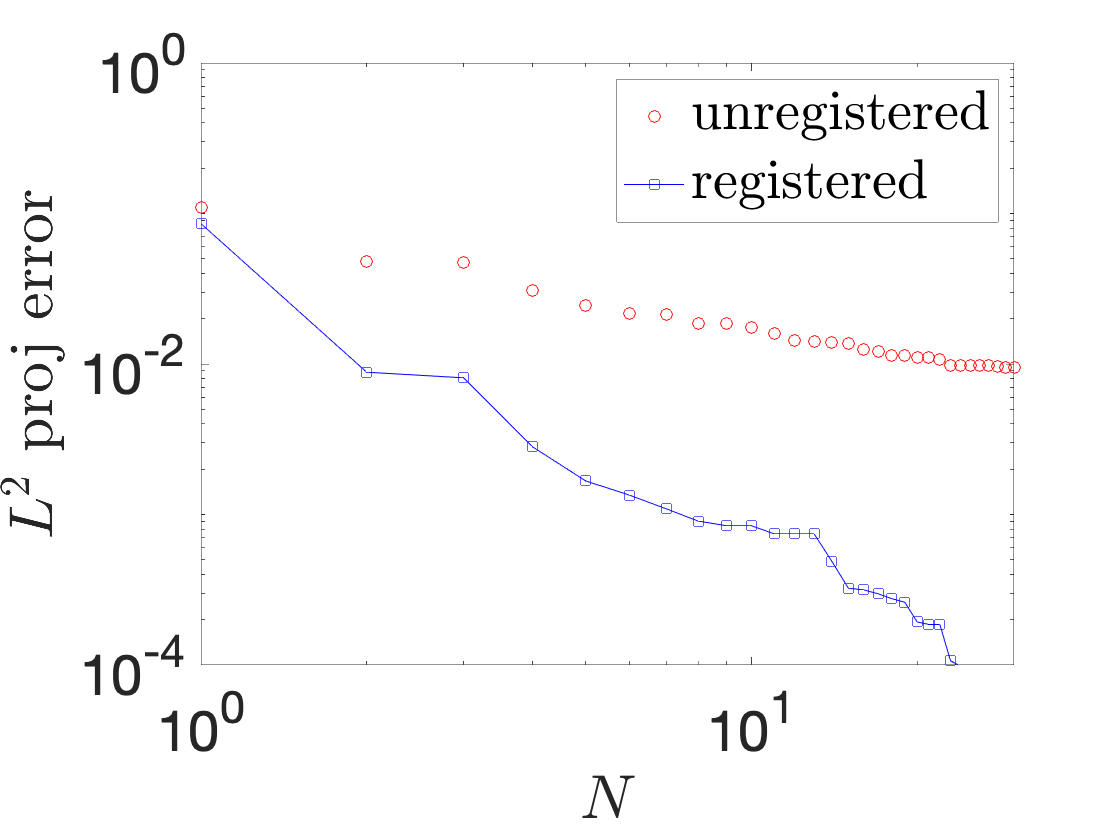
space-time registration for shallow water equations. (a)-(b) free surface for two different parameters and two different time instants. (c) out-of-sample projection error with and without registration.: In , Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain Ω\Omega and the states U0,U1:Ω→ℝU_0,U_1:\Omega \rightarrow \mathbb {R}, we aim to determine an interpolation U^:[0,1]×Ω→ℝ\widehat{U}:[0,1] \times \Omega \rightarrow \mathbb {R} such that U^(0,·)=U0\widehat{U}(0,\cdot ) = U_0 and U^(1,·)=U1\widehat{U}(1,\cdot ) = U_1. The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define U^\widehat{U}. The mapping built at step (ii) might not satisfy the bijectivity constraint in Ω\Omega : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
space-time registration for shallow water equations. (a)-(b) free surface for two different parameters and two different time instants. (c) out-of-sample projection error with and without registration.: In , Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain Ω\Omega and the states U0,U1:Ω→ℝU_0,U_1:\Omega \rightarrow \mathbb {R}, we aim to determine an interpolation U^:[0,1]×Ω→ℝ\widehat{U}:[0,1] \times \Omega \rightarrow \mathbb {R} such that U^(0,·)=U0\widehat{U}(0,\cdot ) = U_0 and U^(1,·)=U1\widehat{U}(1,\cdot ) = U_1. The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define U^\widehat{U}. The mapping built at step (ii) might not satisfy the bijectivity constraint in Ω\Omega : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
space-time registration for shallow water equations. (a)-(b) free surface for two different parameters and two different time instants. (c) out-of-sample projection error with and without registration.: In , Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain Ω\Omega and the states U0,U1:Ω→ℝU_0,U_1:\Omega \rightarrow \mathbb {R}, we aim to determine an interpolation U^:[0,1]×Ω→ℝ\widehat{U}:[0,1] \times \Omega \rightarrow \mathbb {R} such that U^(0,·)=U0\widehat{U}(0,\cdot ) = U_0 and U^(1,·)=U1\widehat{U}(1,\cdot ) = U_1. The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define U^\widehat{U}. The mapping built at step (ii) might not satisfy the bijectivity constraint in Ω\Omega : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
In 21, Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain and the states , we aim to determine an interpolation such that and . The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define . The mapping built at step (ii) might not satisfy the bijectivity constraint in : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
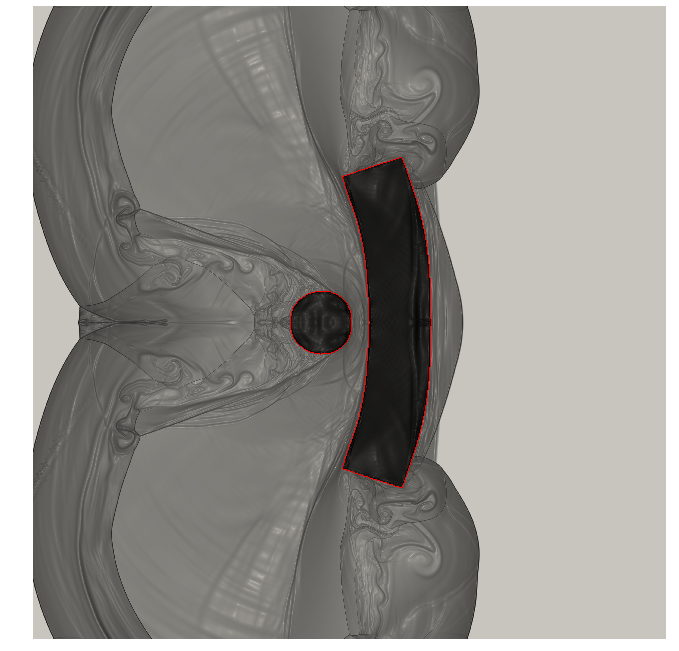
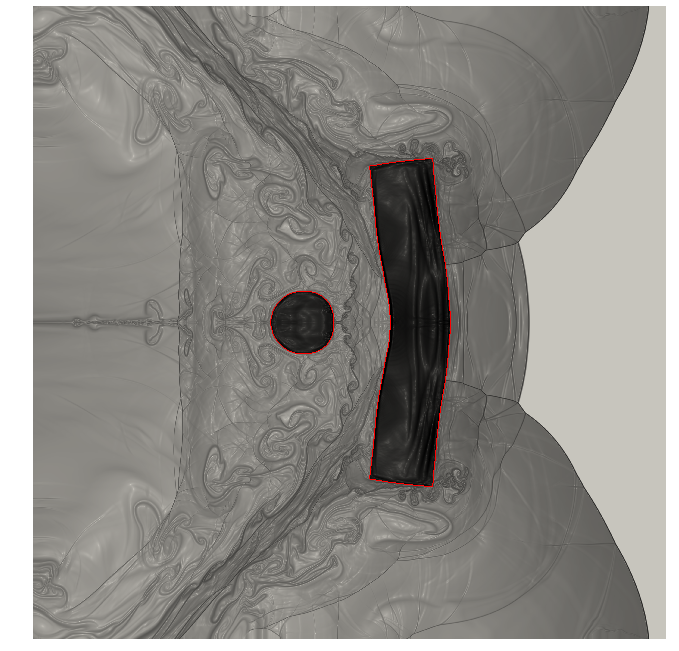
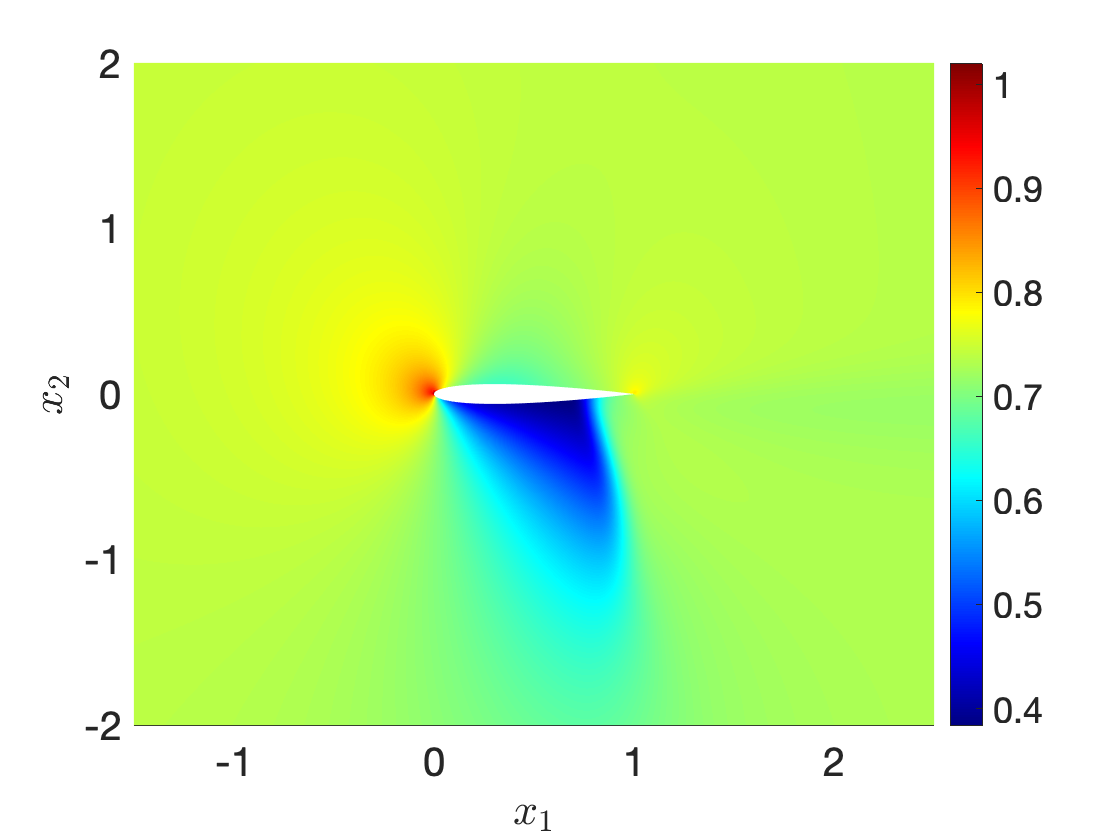
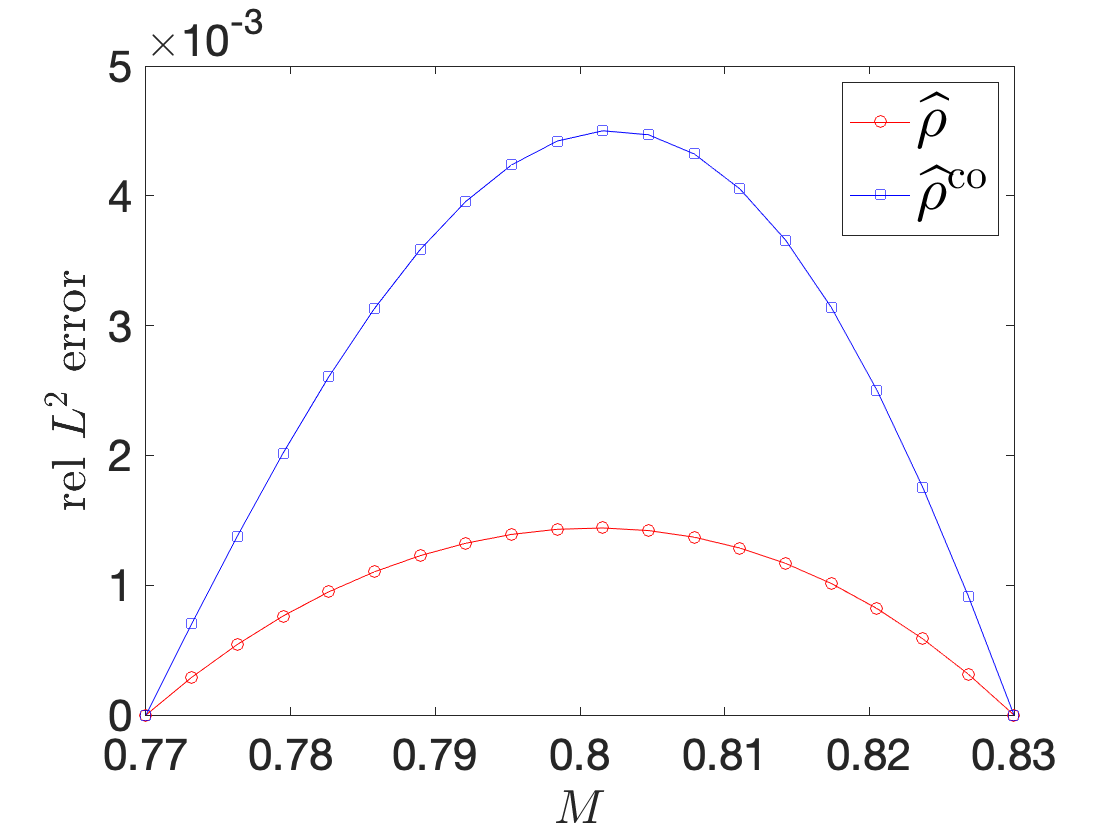
Figure 9 illustrates performance of our procedure for a compressible inviscid flow past a NACA0012 profile at angle of attack 4o for varying free-stream Mach number between and . Figures 9(a) and 9(b) show the fluid density for and , while Figure 9(c) shows an interpolation for an intermediate Mach number: we observe that the nonlinear interpolation smoothly deforms the shock attached to the airfoil. Figure 9(d) compares performance of the nonlinear interpolation with the linear convex interpolation : we observe that the proposed nonlinear interpolation is significantly more accurate than linear interpolation, for the same amount of high-fidelity information.
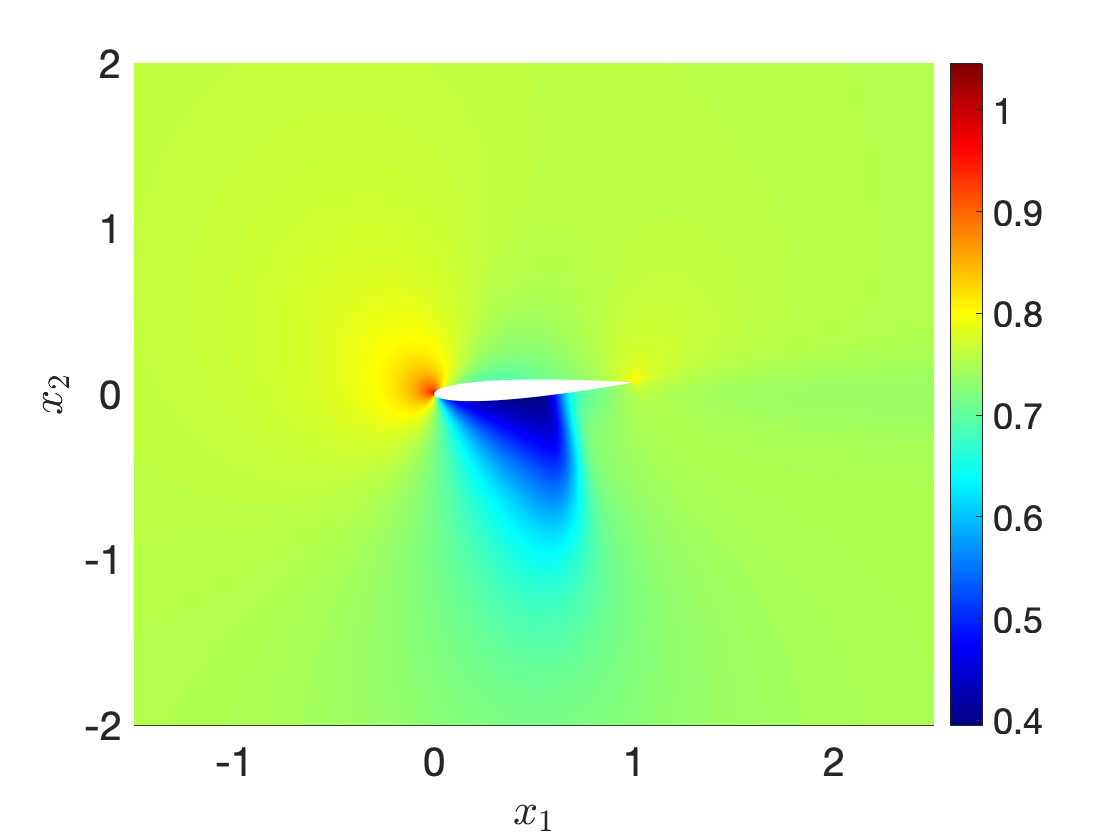
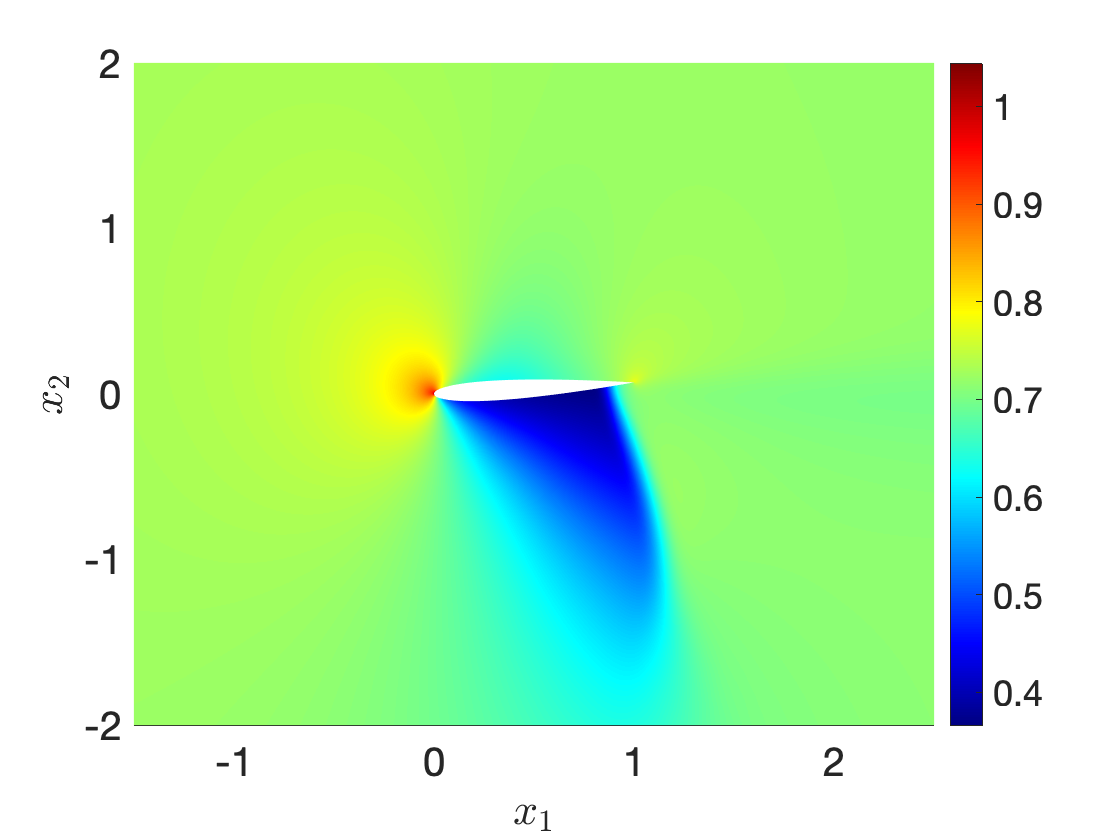
Ma=0.77Ma=0.77
Ma=0.83Ma=0.83
Ma=0.8Ma=0.8 (int)
7.3 Fluid-structure interactions on AMR-enabled quadree grids
Participants: Michel Bergmann, Antoine Fontaneche, Angelo Iollo.
A versatile fully Eulerian method has been developed for the simulation of fluid-structure interaction problems in two dimensions, involving stiff hyper-elastic materials 14. The unified single continuum model is solved in a monolithic way using a quadtree-based Finite Volume scheme, built on very compact discretizations. In the context of fictitious domain methods, the geometry of a structure is captured through a level-set formalism, which enables to define a diffuse fluid-structure interface.
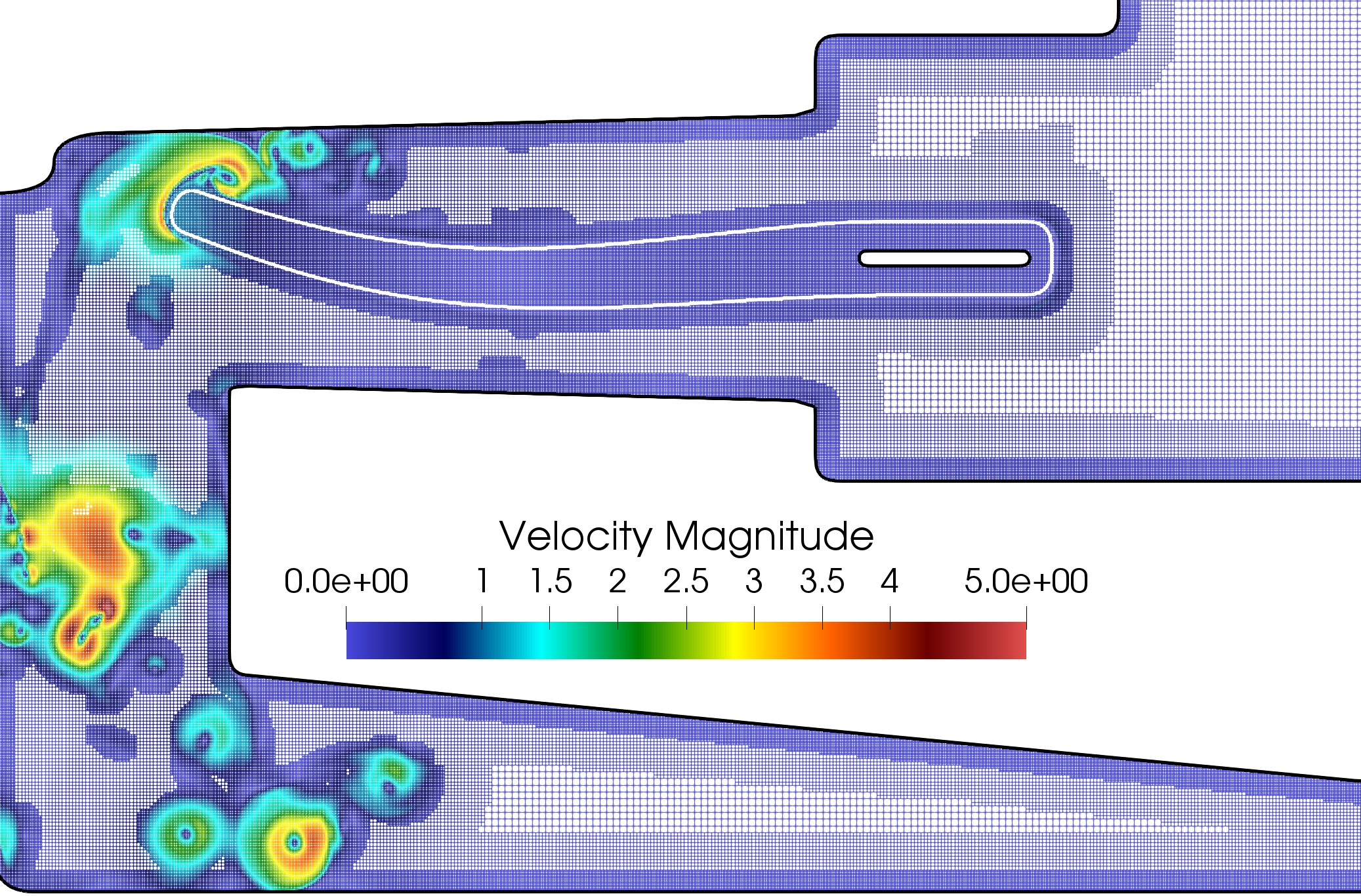
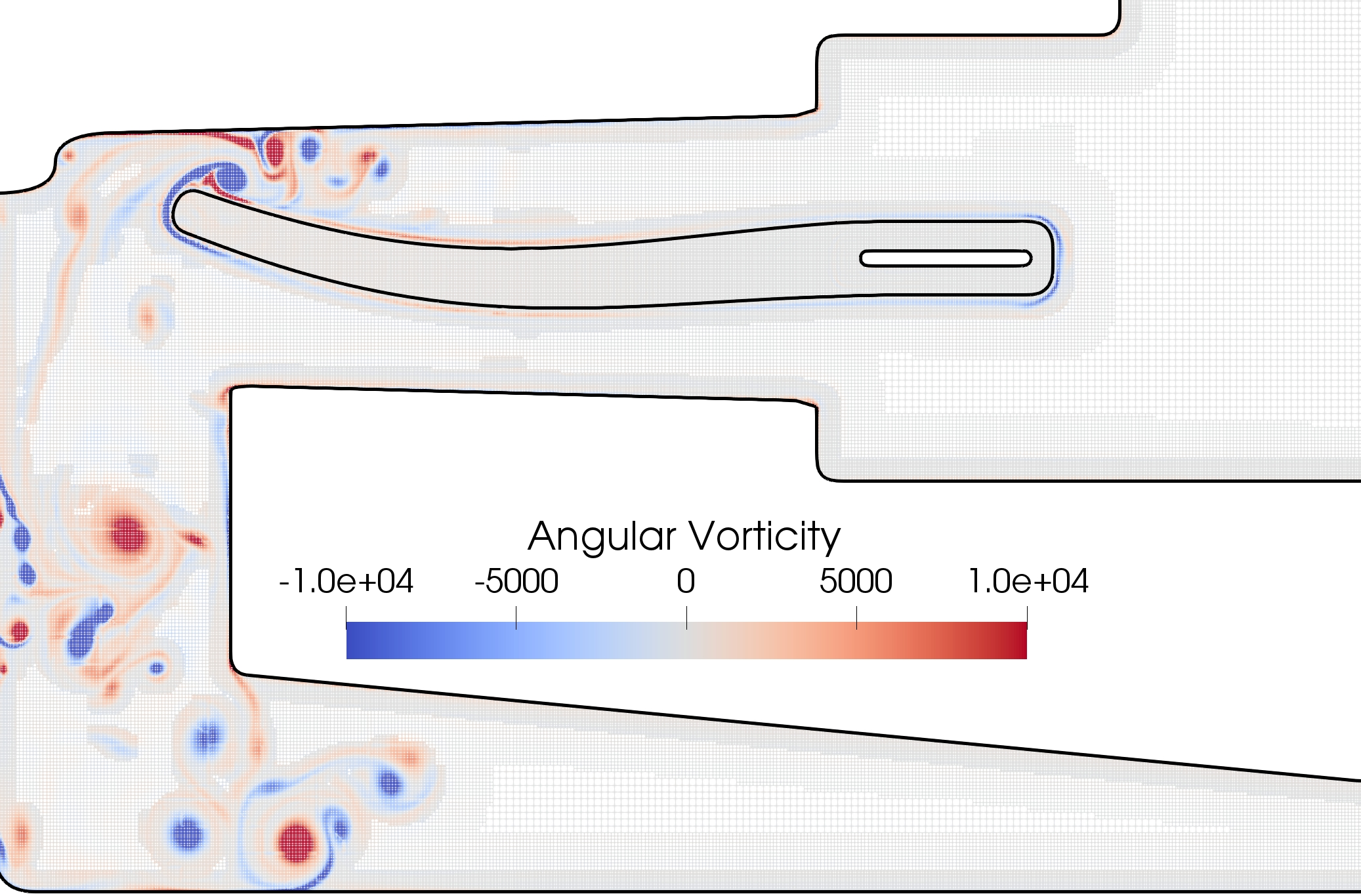
The numerical method has been validated with respect to the literature and the benefits obtained in terms of computational costs through the use of dynamic adaptive meshes has been highlighted. The low impact of coarsening on the structure deformation has been emphasized and the results suggest that the numerical method offers a valuable compromise between accuracy and feasibility of the simulation. As depicted in Figure 10, the simulation of a two-dimensional axi-symmetric flow in a cardiac assist device (LVAD geometry) has finally been proposed as a biomedical application. One paper is submitted.
7.4 Aortic aneurysms: automatic segmentation and registration
Participants: Angelo Iollo, Gwlady Ravon, Sebastien Riffaud, Ludovica Saccaro.
In 35, we developed a new artificial neural network to automatically segment aortic aneurysm. The main idea with this approach was to consider each pixel of the image individually and to see if a model could learn how to categorize it as lumen only from its own intensity and the intensity of its 26 neighbors. We tested different inputs (values, means, variances...) and architectures: a sequential model was retained. For the input, each sample is a vector of 27 intensity values. Only pixels whose intensity is between 100 and 700 are kept for training and prediction.
The second axis of development concerned registration. When a patient have several scans taken at different times, the segmentations are not in the same frame so any comparison would be complicated. The objective was to bring the second segmentation in the frame of the first one. We tested different points-based approaches: register the centerline of the segmentation or the geometry; consider only the lumen or the entire aneurysm. The best results were obtained with the surface of the aneurysm and the iterative closest point algorithm. Once the registration is performed (Figure 11) we can visualize how the aneurysm evolved.
In her PhD, Ludovica Saccaro is developing a data augmentation procedure that takes as input a dataset of patient-specific geometries of aortic aneurisms and returns a larger dataset of in-silico geometries: the objective is to generate large datasets of simulations for statistical analyses. The key elements of the approach are twofold: first, a registration technique based on the identification of the vessel's centerline and of the aortic wall, to determine a rigorous parameterization of the geometries; second, a machine learning technique for data augmentation based on Gaussian mixture models.
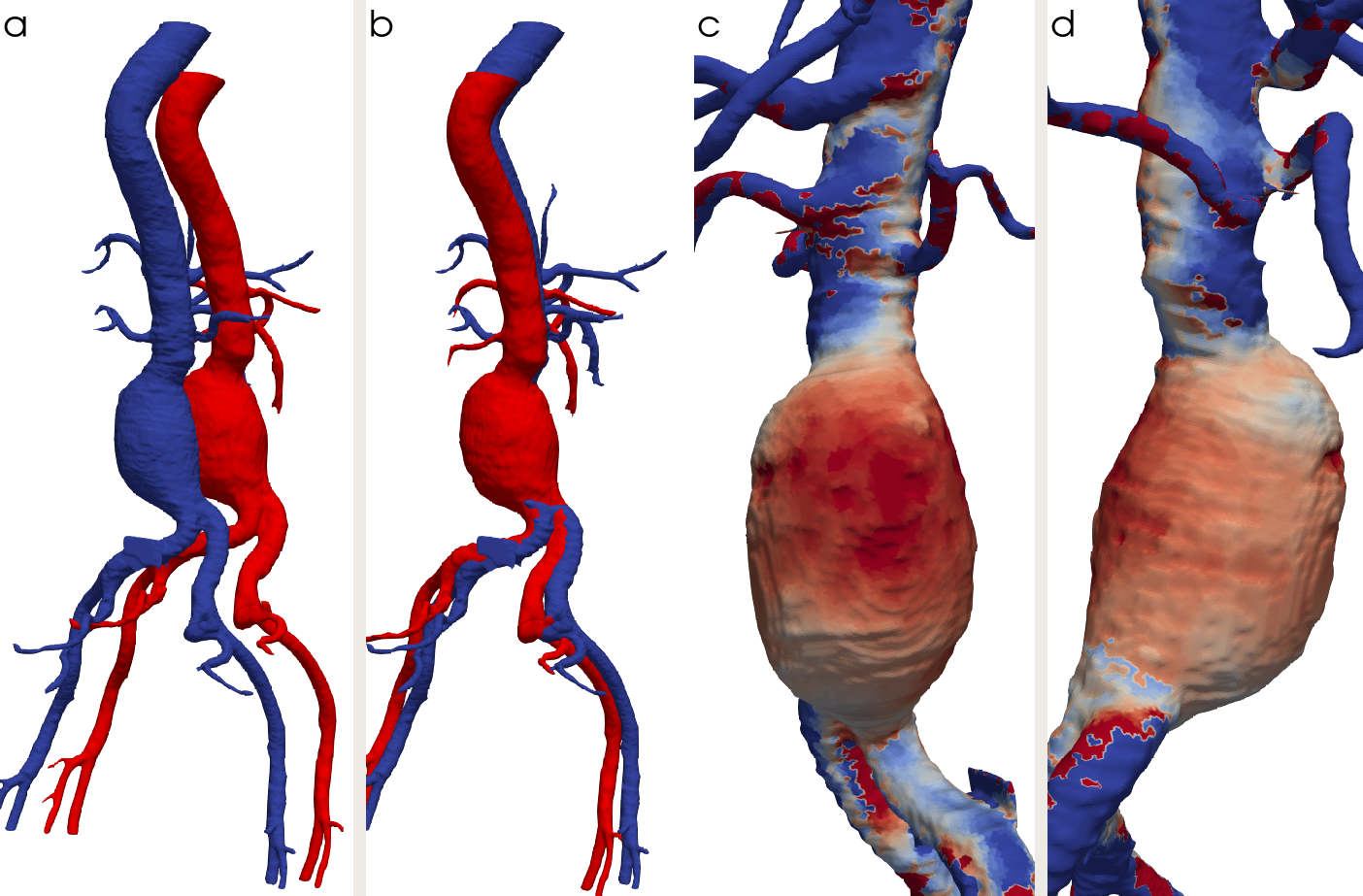
Aneurysm geometries
7.5 Deep learning wall laws for aerodynamic simulations
Participants: Michel Bergmann, Thomas Philibert, Angelo Iollo, Michele Romanelli.
The availability of reliable and accurate wall laws is one of the main challenges of modern CFD. Considering the wide range of phenomena that can be modeled thanks to the flexibility of neural networks, they show an undeniable potential in their application to the modeling of wall flows. Our goal is, therefore, to propose a wall law based on deep learning algorithms with input and output variables of neural networks that conform to classical wall models. Neural networks are thus trained using wall-resolved data in order to reconstruct dimensionless velocity evolution within the boundary layer. Our first methodological approach consists in a new wall law based on deep learning, which shows good performance in modeling the near-equilibrium boundary layer. Near-separation boundary layers are found to be more challenging for deep learning; they are hence the subject of ongoing investigations in the next months.
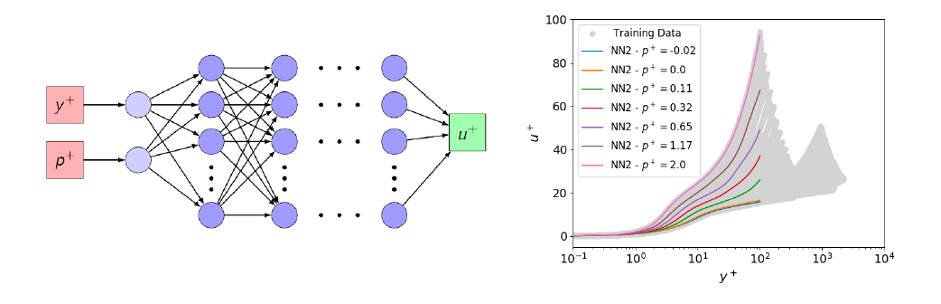
wall law
The SST k-omega model is one of the most used models in industry but suffers from limitations especially when there are separations or transitions. In fig. 13 the error for the Reynold tensor obtained with the SST k-omega model (left) and the error of the Reynold tensor of the same model (compared to the tensor obtained by DNS) but where a correction was added(right) obtained thanks to a neural network. The correction model is based on the strain and stress tensors to build a tensor base starting from algebraic invariants. This basis ensures Galilean invariance. The neural network was trained on 23 different geometries. We present here the results for 2 geometries belonging to the test set (not used for training). The results show a clear improvement of the error compared to the DNS data.
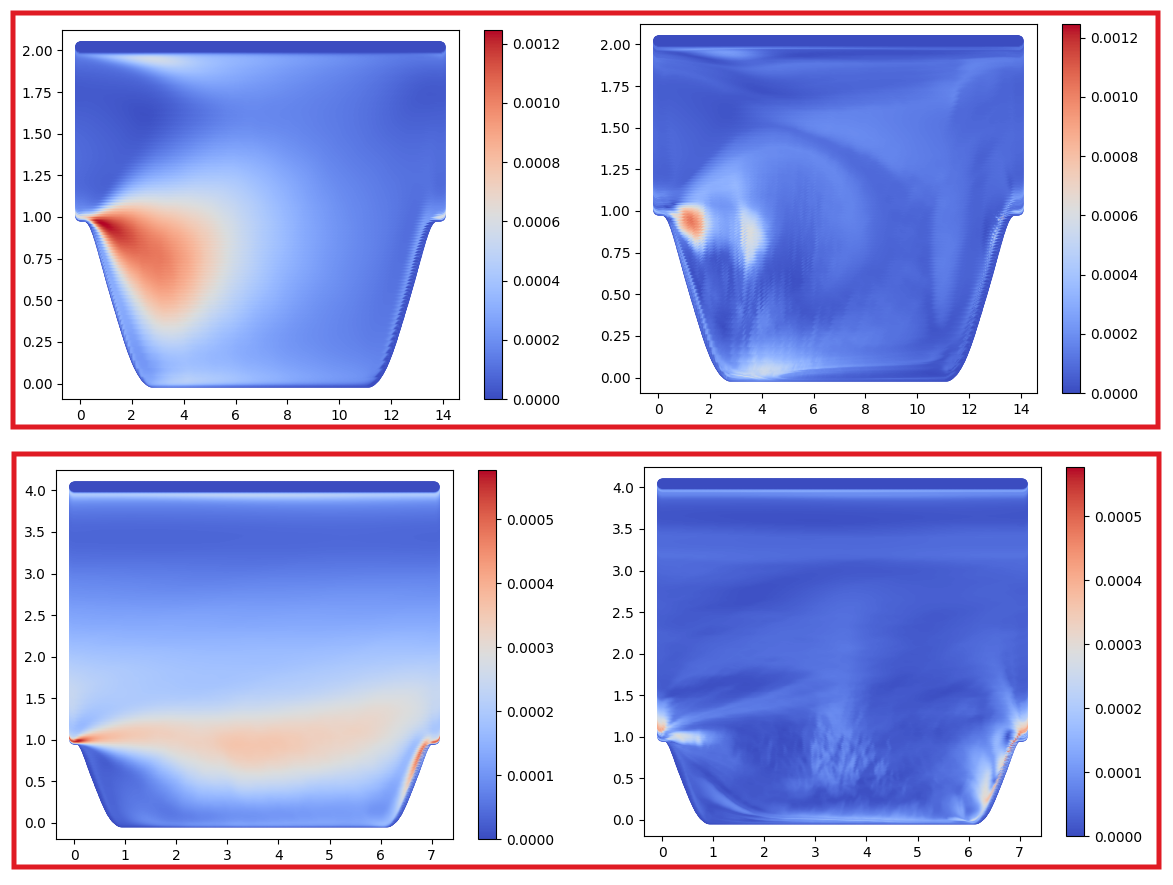
wall law
7.6 Projection-based model order reduction for parametric quasi-static nonlinear mechanics using an open-source industrial code
Participants: Eki Agouzal, Michel Bergmann, Tommaso Taddei.
In 30, we proposed a projection-based model order reduction procedure for a general class of parametric quasi-static problems in nonlinear mechanics with internal variables; the methodology is integrated in the industrial finite element code Code Aster. We developed an adaptive algorithm based on a POD-Greedy strategy, and we developed an hyper-reduction strategy based on an element-wise empirical quadrature, in order to speed up the assembly costs of the ROM by building an appropriate reduced mesh. We introduced a cost-efficient error indicator which relies on the reconstruction of the stress field by a Gappy-POD strategy. We presented numerical results for a three-dimensional elastoplastic system in order to illustrate and validate the methodology.
8 Partnerships and cooperations
8.1 International initiatives
8.1.1 Associate Teams in the framework of an Inria International Lab or in the framework of an Inria International Program
Participants: Michel Bergmann, Angelo Iollo, Tommaso Taddei.
MARE
-
Title:
Multiscale Accurate Reduced-order model Enablers
-
Duration:
2019 -> 2022
-
Coordinator:
Charbel Farhat (cfarhat@stanford.edu)
-
Partners:
- Stanford University Stanford (États-Unis)
-
Inria contact:
Angelo Iollo
-
Summary:
Reduced-order models (ROMs) are simplified mathematical models derived from the full set of partial differential equations governing the physics of the phenomenon of interest. We focus on ROMs that are data-driven as they are based on relevant solution data previously obtained. In particular we will focus on multiscale adaptive models where the large scales are governed by a PDE and the small scales are described by data driven models. To do that we will leverage on tools from data geometry, numerical PDEs and machine learning.
8.2 European initiatives
8.2.1 H2020 projects
ARIA
ARIA project on cordis.europa.eu
-
Title:
Accurate Roms for Industrial Applications
-
Duration:
From December 1, 2019 to November 30, 2024
-
Partners:
- INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET AUTOMATIQUE (INRIA), France
- ESTECO SPA (ESTECO), Italy
- NUREA (NUREA), France
- VALOREM SAS (valorem), France
- SCUOLA INTERNAZIONALE SUPERIORE DI STUDI AVANZATI DI TRIESTE (SISSA), Italy
- IEFLUIDS S.R.L. (IEFLUIDS S.R.L.), Italy
- POLITECNICO DI TORINO (POLITO), Italy
- POLITECNICO DI MILANO (POLIMI), Italy
- OPTIMAD ENGINEERING SRL (Optimad srl), Italy
- UNIVERSITY OF SOUTH CAROLINA (USC), United States
- VOLKSWAGEN AKTIENGESELLSCHAFT (VW AG), Germany
- VIRTUALMECHANICS SL (VM), Spain
- VIRGINIA POLYTECHNIC INSTITUTE AND STATE UNIVERSITY (VT), United States
- UNIVERSITA CATTOLICA DEL SACRO CUORE (UCSC), Italy
- BOARD OF TRUSTEES OF THE LELAND STANFORD JUNIOR UNIVERSITY (STANFORD), United States
- UNIVERSIDAD DE SEVILLA, Spain
-
Inria contact:
Angelo IOLLO
-
Coordinator:
Angelo IOLLO
-
Summary:
The project Accurate Roms for Industrial Applications aims at developing an array of mathematical methods for constructing predictive reduced-order models (ROMs) with guaranteed accuracy, robustness, reliability and efficiency for applications involving complex physical phenomena. New approaches to this challenge are proposed here with a focus on the Euler and Navier–Stokes equations of fluid flow, two of the most challenging continuum models with an extraordinary rich range of industrial applications. The mathematical modeling and solution of the Euler and Navier-Stokes equations is sometimes cited as the greatest challenge in continuum modeling of physical phenomena. This topic is selected as our principal focus because of its intrinsic importance, but also because the mathematical methods developed in addressing this very challenging task may well have an impact on other fields of knowledge. We plan to tackle these challenging objectives in this staff exchange program by combining the unique expertise of our extended research team whose members have made significant progress in ROM research during the past decade. This academic expertise is cross-fertilized by the exchange with knowledge intensive SMEs ans start up and well established industrial partners that will benefit from the scientific and technological results of the team and will challenge the solutions found with applications in real world problems.
8.3 National initiatives
- ANR (national agency for research funding) DRAGON2.
- Partners : CNRS/Université de Poitiers/Inria. 27 k€+ 1 PhD.
- The goal is study the aquatic swimming a several snakes using biomimetism and bioinspiration. In this project, we have experimental data for snake swimming, and we are building a numerical twin to compute integral quantities like the efficiency. Reinforcement learning is also considered to optimize the snake swimming.
- Inria Exploratory Action: AM2OR (Adaptive meshes for model order reduction).
- Principal investigators: Nicolas Barral (Inria team: Cardamom), Tommaso Taddei. 14 k€+ 1 PhD + 1 PostDoc.
- Mesh adaptation and model order reduction both aim at reducing significantly the computational cost of numerical simulations by taking advantage of the solution's features. Model order reduction is a method that builds lighter surrogate models of a system's response over a range of parameters, which is particularly useful in the solution of design and optimization inverse problems. Reduced-order models rely on a high-fidelity (e.g., finite element) approximation that should be sufficiently accurate over the whole range of parameters considered: in presence of structures such as shocks and boundary layers, standard mesh refinement techniques would lead to high-fidelity models of intractable size. In this project, we propose a novel adaptive procedure to simultaneously construct a high-fidelity mesh (and associated discretisation) and a reduced-order model for a range of parameters, with particular emphasis on inverse problems in computational fluid dynamics.
8.4 Regional initiatives
Chaire PROVE (cf. section 6).
9 Dissemination
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
Michel Bergmann, Angelo Iollo and Tommaso Taddei organized a three-day workshop in Bordeaux from 30/03/2022 to 01/04/2022. The workshop aimed at tightening the link between fundamental research on model reduction and clinical and industrial applications. Topics of the presentations included reduced basis methods for parameterized systems, proper orthogonal decomposition, nonlinear compression methods, data assimilation and geometry inference methods. This workshop was supported by: Inria - EDF - Bordeaux INP - Université de Bordeaux - CNRS- IdEx - HORIZON H2020
9.1.2 Invited talks
- Angelo Iollo: November 14-18. Some numerical models for multi-material interaction in compressible or incompressible regime. Numerical methods for fluid-structure interaction problems.
- Angelo Iollo: January 24. Mapping of coherent structures in parameterized flows by learning optimal transportation with Gaussian models. Institut Henri Poincaré. Seminar CEA/GAMNI computational fluid dynamics.
- Angelo Iollo: July, 6-8. Discussion of some examples of linear or nonlinear, intrusive or non-intrusive reduced models based on Convex Displacement Interpolation. ARIA-VT workshop.
- Angelo Iollo: July 26. Some examples of linear or nonlinear, intrusive or non-intrusive reduced models based on convex displacement interpolation. 1st International Forum for Artificial Intelligence in Mechanical Engineering, Shenzhen, China (Virtual) .
- Tommaso Taddei: July, 6-8. Registration-based model reduction of parameterized PDEs with spatio-parameter adaptivity. ARIA-VT workshop.
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
Two members of the team are Professor (Angelo Iollo) or Assistant Professor (Afaf Bouharguane) at Université de Bordeaux and have teaching duties, which consist in courses and practical exercises in numerical analysis and scientific computing. Michel Bergmann (CR) also teaches around 64 hours per year (practical exercises in programming for scientific computing). Tommaso Taddei (CR) also teaches around 50 hours per year (practical exercises in numerical analysis and scientific computing).
9.2.2 Juries
Angelo Iollo: Reviewer of the PhD theses of (i) Elena Travaglia (University of Torino) 06/04/2022, (ii) Serena Costanzo (Sorbonne) 22/06/2022, (iii) Antonietta Conte (Politecnico di Torino), 13/04/2022, (iv) Nadine Dirani (University of Nice) 7/12/2022. Review of the HDR thesis of Thibault Dairy (CNAM Paris) 21/11/2022.
10 Scientific production
10.1 Major publications
- 1 articleAn all-speed relaxation scheme for gases and compressible materials.Journal of Computational Physics3512017, 1-24
- 2 articleFluid--solid Floquet stability analysis of self-propelled heaving foils.Journal of Fluid Mechanics9102021, A28
- 3 articleEnablers for robust POD models.Journal of Computational Physics22822009, 516--538
- 4 articleAn accurate cartesian method for incompressible flows with moving boundaries.Communications in Computational Physics1552014, 1266--1290
- 5 articleBioinspired swimming simulations.Journal of Computational Physics3232016, 310 - 321
- 6 articleModeling and simulation of fish-like swimming.Journal of Computational Physics23022011, 329 - 348
- 7 articleAccurate Asymptotic Preserving Boundary Conditions for Kinetic Equations on Cartesian Grids.Journal of Scientific Computing2015, 34
- 8 articleNumerical solution of the Monge--Kantorovich problem by density lift-up continuation.ESAIM: Mathematical Modelling and Numerical Analysis4961577November 2015
- 9 articleA Cartesian Scheme for Compressible Multimaterial Models in 3D.Journal of Computational Physics3132016, 121-143
- 10 articleEnablers for high-order level set methods in fluid mechanics.International Journal for Numerical Methods in Fluids79December 2015, 654-675
10.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Scientific book chapters
Edition (books, proceedings, special issue of a journal)
Reports & preprints
10.3 Cited publications
- 38 articleA penalization method to take into account obstacles in a incompressible flow.Numerische Mathematik8141999, 497-520
- 39 articleExact and approximate solutions of Riemann problems in non-linear elasticity.Journal of Computational Physics228182009, 7046-7068
- 40 articleA Cartesian scheme for compressible multimaterial models in 3D.Journal of Computational Physics3132016, 121-143URL: http://www.sciencedirect.com/science/article/pii/S0021999116000966
- 41 articleAn experimental study of entrainment and transport in the turbulent near wake of a circular cylinder.Journal of fluid mechanics1361983, 321--374
- 42 articleModelling wave dynamics of compressible elastic materials.Journal of Computational Physics22752008, 2941-2969
- 43 bookElements of continuum mechanics.Nauka Moscow1978
- 44 phdthesisConstruction d'une chaîne d'outils numériques pour la conception aérodynamique de pales d'éoliennes.Université de Bordeaux2014
- 45 articleA Conservative Three-Dimensional Eulerian Method for Coupled Solid-Fluid Shock Capturing.Journal of Computational Physics18312002, 26-82
- 46 bookLevel Set Methods and Fast Marching Methods.Cambridge University Press, Cambridge, UK1999
- 47 articleA registration method for model order reduction: data compression and geometry reduction.SIAM Journal on Scientific Computing4222020, A997--A1027
- 48 articleRegistration-based model reduction in complex two-dimensional geometries.submitted to Journal of Scientific Computing2021
- 49 articleSpace-time registration-based model reduction of parameterized one-dimensional hyperbolic PDEs.ESAIM: Mathematical Modelling and Numerical Analysis (accepted)2020

