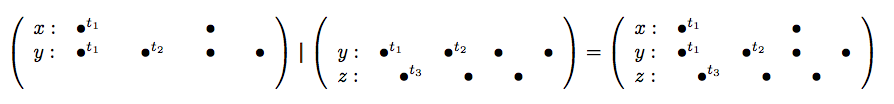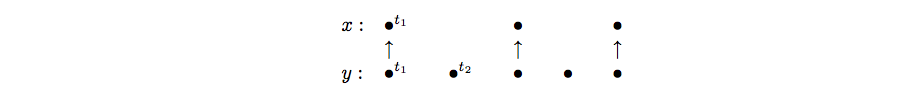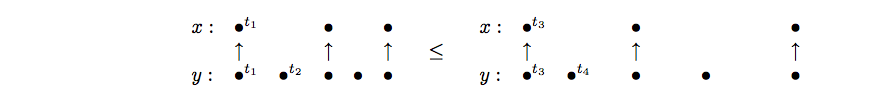Section: Scientific Foundations

Polychronous model of computation

We consider a partially-ordered set of tags $t$ to denote instants seen as symbolic periods in time during which a reaction takes place. The relation $t_1\le t_2$ says that $t_1$ occurs before $t_2$. Its minimum is noted 0. A totally ordered set of tags $C$ is called a chain and denotes the sampling of a possibly continuous or dense signal over a countable series of causally related tags. Events, signals, behaviors and processes are defined as follows:

• an event $e$ is a pair consisting of a value $v$ and a tag $t$,

• a signal $s$ is a function from a chain of tags to a set of values,

• a behavior $b$ is a function from a set of names $x$ to signals,

• a process $p$ is a set of behaviors that have the same domain.

In the remainder, we write $\mathrm{tags}\left(s\right)$ for the tags of a signal $s$, $\mathrm{vars}\left(b\right)$ for the domain of $b$, ${b|}_X$ for the projection of a behavior $b$ on a set of names $X$ and $b/X$ for its complementary.

Figure 1 depicts a behavior $b$ over three signals named $x$, $y$ and $z$. Two frames depict timing domains formalized by chains of tags. Signals $x$ and $y$ belong to the same timing domain: $x$ is a down-sampling of $y$. Its events are synchronous to odd occurrences of events along $y$ and share the same tags, e.g. $t_1$. Even tags of $y$, e.g. $t_2$, are ordered along its chain, e.g. $t_1<t_2$, but absent from $x$. Signal $z$ belongs to a different timing domain. Its tags are not ordered with respect to the chain of $y$.

Figure 1. Behavior $b$ over three signals $x$, $y$ and $z$ in two clock domains

Composition

Synchronous composition is noted $p|q$ and defined by the union $b\cup c$ of all behaviors $b$ (from $p$) and $c$ (from $q$) which hold the same values at the same tags ${b|}_I{=c|}_I$ for all signal $x\in I=\mathrm{vars}\left(b\right)\cap \mathrm{vars}\left(c\right)$ they share. Figure 2 depicts the synchronous composition (Figure 2 , right) of the behaviors $b$ (Figure 2 , left) and the behavior $c$ (Figure 2 , middle). The signal $y$, shared by $b$ and $c$, carries the same tags and the same values in both $b$ and $c$. Hence, $b\cup c$ defines the synchronous composition of $b$ and $c$.

Figure 2. Synchronous composition of $b\in p$ and $c\in q$

Scheduling

A scheduling structure is defined to schedule the occurrence of events along signals during an instant $t$. A scheduling $\to$ is a pre-order relation between dates $x_t$ where $t$ represents the time and $x$ the location of the event. Figure 3 depicts such a relation superimposed to the signals $x$ and $y$ of Figure 1 . The relation $y_{t_1}\to x_{t_1}$, for instance, requires $y$ to be calculated before $x$ at the instant $t_1$. Naturally, scheduling is contained in time: if $t<t^{\text{'}}$ then $x_t{\to }^b{x}_{t^{\text{'}}}$ for any $x$ and $b$ and if $x_t{\to }^b{x}_{t^{\text{'}}}$ then $t^{\text{'}}\neg <t$.

Figure 3. Scheduling relations between simultaneous events

Structure

A synchronous structure is defined by a semi-lattice structure to denote behaviors that have the same timing structure. The intuition behind this relation is depicted in Figure 4 . It is to consider a signal as an elastic with ordered marks on it (tags). If the elastic is stretched, marks remain in the same relative (partial) order but have more space (time) between each other. The same holds for a set of elastics: a behavior. If elastics are equally stretched, the order between marks is unchanged.

In Figure 4 , the time scale of $x$ and $y$ changes but the partial timing and scheduling relations are preserved. Stretching is a partial-order relation which defines clock equivalence. Formally, a behavior $c$ is a stretching of $b$ of same domain, written $b\le c$, iff there exists an increasing bijection on tags $f$ that preserves the timing and scheduling relations. If so, $c$ is the image of $b$ by $f$. Last, the behaviors $b$ and $c$ are said clock-equivalent, written $b\sim c$, iff there exists a behavior $d$ s.t. $d\le b$ and $d\le c$.

Figure 4. Relating synchronous behaviors by stretching.