Section: New Results

Matching problems and their applications

Participants : Laurent Baratchart, Martine Olivi, Gibin Bose, David Martinez Martinez, Fabien Seyfert.

Filter synthesis is usually performed under the hypothesis that both ports of the filter are loaded on a constant resistive load (usually 50 Ohm). In complex systems, filters are however cascaded with other devices, and end up being loaded, at least at one port, on a non purely resistive frequency varying load. For example, in an emitter-receiver, the antenna is followed by a filter. Whereas the antenna can usually be regarded as a resistive load at some frequencies, this is far from being true on the whole pass-band. A mismatch between the antenna and the filter, however, causes irremediable power losses, both in emission and transmission. Antennas are not the only systems where matching is of importance: in multiplexer design, one of the most complicated problems among microwave device synthesis, each filter is plugged at one of its accesses on a load made of the common manifold and all other channel filters. This load is far from being matched, and leads to a complex simultaneous matching problem, of all filters connected via the common manifold junction. Our goal is therefore to develop a method for filter synthesis that allows us to match varying loads on specific frequency bands, while enforcing some rejection properties away from the pass-band.

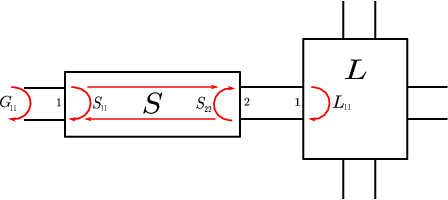
Figure 5 shows a filter with scattering matrix $S$, plugged at its right port on a frequency varying load with reflection parameter $L_{1,1}$. If the filter is lossless, simple algebraic manipulations show that on the frequency axis the reflex-ion parameter satisfies:

The matching problem of minimizing $|G_{1,1}|$ amounts therefore to minimize the pseudo-hyperbolic distance $\delta$ between the filter's reflection parameter $S_{2,2}$ and the conjugate of the load's reflection $\overline{L_{1,1}}$, on a given frequency band. On the contrary enforcing a rejection level on a stop band, amounts to maintaining the value of $\delta (L_{1,1},S_{2,2})$ above a certain threshold on this frequency band. For a broad class of filters, namely those that can be modeled by a circuit of $n$ coupled resonators, the scattering matrix $S$ is a rational function of McMillan degree $n$ in the frequency variable. The matching problem thus appears to be a rational approximation problem in the hyperbolic metric.

Multiplexer synthesis via interpolation and common junction design

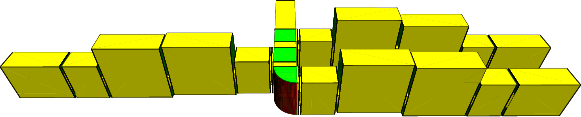
Based on our work linking Nevanlinna-Pick interpolation and point-wise matching techniques [6] we tackled the synthesis of a multiplexer on the basis of frequency specifications relative to a triplexer furnished by CNES and deemed to be problematic. Theoretical results guaranty the existence in this case, under a strict contractivity hypothesis on the common junction, of a simultaneous pointwise matching solution of all three channel filters. This result is however not constructive as it relies on Brouwer's fixed point theorem, a purely topological argument. In the context of the PhD of D. Martinez, we developed a continuation algorithm, starting from a completely decoupling junction and ending up with the manifold junction of interest. When the junction decouples all the channels, the overall matching problem results in 3 independent Nevanlinna-Pick interpolation problems as described in [6]: this yield the starting point of our continuation approach. The manifold peaks have also been identified as crucial here: these are resonances taking place in the common junction of the multiplexer, at which transmission of energy becomes impossible between a given channel and the common port. These peaks have been mathematically characterized, and a systematic combinatorial algorithm designed for the synthesis of a “peak free” manifold junction. In particular it was proven, that an extremely compact junction is needed to fit the specifications furnished by CNES: when dispersive effects increase (and they do with the size of the junction) the appearance of manifold peaks has been proven inevitable. Using a continuation approach to compute the channel filters responses and a combinatorial procedure to design a peak-free junction, a complete triplexer has been synthesized that fits the CNES specifications. The synthesis was first considered in terms of circuits and eventually transformed in a real hardware realized in waveguide technology (see Figure.6 ). The latter is currently being manufactured at XLIM laboratories, where our colleague S. Bila is co-advising D. Martinez' PhD.

Uniform matching and global optimality considerations

The interpolation procedure of [6] provides us with matching/rejecting filtering characteristics at a discrete set of frequencies. It can serve as a starting point for heavier optimization procedures, where the matching and rejection specifications are expressed uniformly over the bandwidth. Although the practical results thus obtained are quite convincing, we have no proof of their global optimality. This has led us to seek alternative approaches allowing us to assess, at least in simple cases, global optimality of the obtained response. By optimality of a response we mean, as in classical filtering, a best match of the response in the uniform norm on a given pass-band, while meeting given rejection constraints on a stop-band, and this for a given maximal degree $n_c$ of the matching network. Following the approach of Fano and Youla, we considered the problem of designing a $2\times 2$ loss-less frequency response, under the condition that a specified load can be “unchained” from one of its port. This classically amounts to set interpolation conditions on the response at the transmission zeros of the Darlington extension of the load. When the load admits a rational representation of degree $n_a=1$, and if the transmission zeros of the overall system are fixed, we were able to show that the uniform matching problem over an interval, together with rejection constraints at other frequency locations, reduces to a convex minimization problem with convex constraints over the set of non-negative polynomials of given degree. When the load is of degree greater than 1, our approach is a convex relaxation of the original problem as the computed matching circuit has in general degree $n_c+n_a-1$. This delivers lower bounds for the original matching problem, the first that are known of this problem under degree constraint.

The internal representation of our problem, relies on the use of a Pick matrix $𝒫$ depending on a positive polynomial $p$, that needs to be positive in terms of matrices, that is $𝒫\left(p\right)⪰0$. Although we know for the convexity of our global formulation [17], the concavity of the matrix valued map $𝒫$ is not evident at all. Using arguments of matrix valued Nevanlinna-Pick interpolation we were able to establish it this years, that is: for all pair of positive polynomials $(p_1,p_2)$ the following holds,

This is an important result, as it justifies the use of Lagrangian relaxation for our problem that appears to be a non-linear, convex, semi-definite optimization program (NLSDP), the hardest class among current convex optimization. We plan to build on this result, in order to obtain a critical point equation to our problem, in terms of extremal points of the involved polynomials.

The software implementation developed within the PhD of D. Martinez, combining logarithmic barrier functions and Lagrangian relaxation techniques has been made available for practitioners as Matlab library called Puma 5.2. Results obtained thank to this tool, have been presented in [15], [18] and on a dedicated workshop at the conference IMS2018. Design of use cases, for antenna matching problems relevant in 5G and IOT applications are currently being analyzed with LEAT, within the context of G. Bose's PhD.